Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Chuyên đề Toán học lớp 7: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
A. Lý thuyết
1. Khái niệm đường thẳng vuông góc, đường xiên, hình chiếu của đường xiên

Từ điểm A không nằm trên đường thẳng thẳng d, kẻ một đường thẳng thẳng vuông góc với d tại H. Khi đó:
• Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng thẳng d; điểm H gọi là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d.
• Lấy một điểm M trên d (M khác H), kẻ đoạn thẳng AM. Đoạn thẳng AM gọi là một đường xiên kẻ từ A đến đường thẳng d.
2. Quan hệ giữa đường vuông góc và đường xiên
Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Ví dụ: AH ⊥ a ⇒ AH < AC, AH < AD
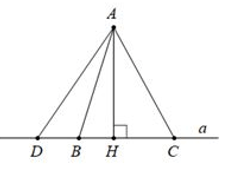
Chú ý: Vì độ dài doạn thẳng AH là ngắn nhất trong các đoạn thẳng kẻ từ A đến a nên độ dài đoạn thẳng AH được gọi là khoảng cách từ điểm A đến đường thẳng d.
3. Các đường xiên và hình chiếu của chúng

Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng thẳng đến đường thẳng thẳng đó:
• Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
AH ⊥ a, HD > HC ⇒ AD > AC
• Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
AH ⊥ a, AD > AC ⇒ HD > HC
• Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
AB = AC ⇔ HB = HC
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Chọn phát biểu sai trong các phát biểu sau:
A. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường lớn nhất.
B. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
C. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn có hình chiếu nhỏ hơn.
D. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Giải thích: Trong các phát biểu, ý A, B, D đều đúng
Ý C sai vì: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn có hình chiếu lớn hơn.
Chọn đáp án C.
Bài 2: Cho ba điểm A, B, C thẳng hàng, B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
A. AH < BH
B. AH < AB
C. AH > BH
D. AH = BH
Giải thích:
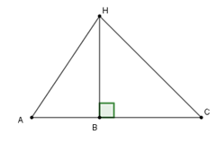
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Chọn đáp án C.
Bài 3: Trong tam giác ABC có chiều cao AH:
A. Nếu BH < HC thì AB < AC
B. Nếu AB < AC thì BH < HC
C. Nếu BH = HC thì AB = AC
D. Cả A, B, C đều đúng
Giải thích:
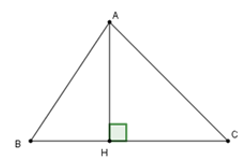
Trong tam giác ABC có AH là đường vuông góc và BH; CH là hai hình chiếu.
Khi đó:
- Nếu BH < HC thì AB < AC
- Nếu AB < AC thì BH < HC
- Nếu BH = HC thì AB = AC
Nên cả A, B, C đều đúng.
Chọn đáp án D.
Bài 4: Cho hình vẽ sau:
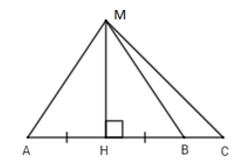
Chọn đáp án sai trong các đáp án sau:
A. MA > MH
B. HB < HC
C. MA = MB
D. MC < MA
Giải thích:
Vì MH là đường vuông góc và MA là đường xiên nên MA > MH (quan hệ đường vuông góc và đường xiên) nên A đúng.
Vì ∠MBC là góc ngoài ΔMHB ⇒ ∠MBC > ∠MHB = 90°
Xét ΔMBC có: ∠MBC là góc tù nên suy ra MC > MB (quan hệ giữa góc và cạnh trong tam giác)
Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC.
⇒ HB < HC (quan hệ giữa đường xiên và hình chiếu) nên B đúng.
Vì AH = HB (gt) mà AH và HB lần lượt là hình chiếu của AM và BM .
⇒ MA = MB (quan hệ giữa đường xiên và hình chiếu) nên C đúng.
Ta có: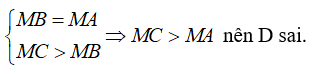
Chọn đáp án D.
Bài 5: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C xuống đường thẳng BM. So sánh BD + BE và AB
A. BD + BE > 2AB
B. BD + BE < 2AB
C. BD + BE = 2AB
D. BD + BE < AB
Giải thích:
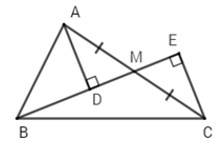
Vì ΔABM vuông tại A (gt) nên BA < BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM = BD + DM ⇒ BA < BD + DM (1)
Mặt khác: BM = BE - ME ⇒ BA < BE - ME (2)
Cộng hai vế của (1) và (2) ta được: 2BA < BD + BE + MD - ME (3)
Vì M là trung điểm của AC (gt) ⇒ AM = MC (tính chất trung điểm)
Xét tam giác vuông ADM và tam giác vuông CEM có:
AM = MC (cmt)
∠AMD = ∠EMC (đối đỉnh)
⇒ ΔADM = ΔCEM (cạnh huyền – góc nhọn)
⇒ MD = ME (4) (2 cạnh tương ứng)
Từ (3) và (4) ⇒ BD + BE > 2AB
Chọn đáp án A.
II. Bài tập tự luận
Bài 1: Cho ΔABC, kẻ AH ⊥ BC tại H, Chứng minh rằng:
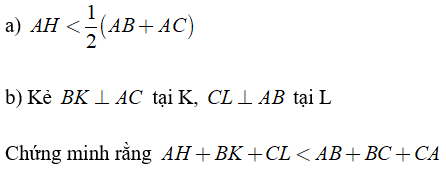
a) Ta có:
AH là đường vuông góc
AB, AC là các đường xiên
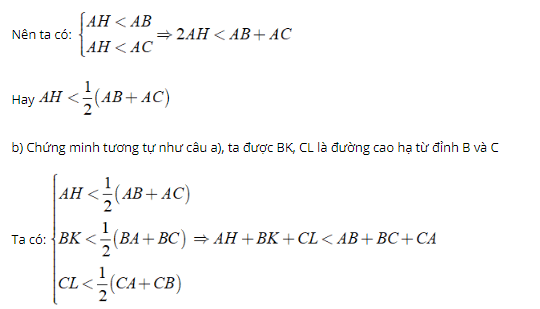
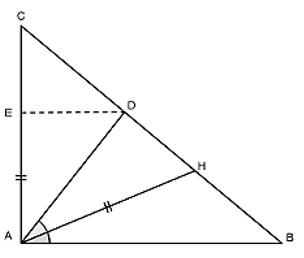
Bài 2: Cho tam giác ABC vuông tại A. Kẻ AH ⊥ BC . Trên cạnh huyền BC lấy điểm D sao cho BD = AB. Trên cạnh AC lấy điểm E sao cho AE = AH.
Chứng minh rằng DE ⊥ AC ⇒ BC + AH > AC + AB .
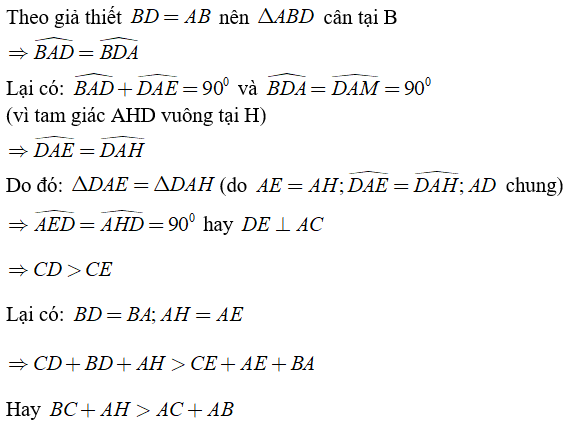
Bài 3: Cho hình thang cân có độ dài đáy nhỏ bằng 4 cm, độ dài đáy lớn gấp đôi độ dài đáy nhỏ. Tính khoảng cách giữa hai đáy của hình thang cân, biết diện tích hình thang cân đó bằng 18 cm.
Bài 4: Cho hình thang ABCD (Hình vẽ) có AB = 7 cm. Gọi E là hình chiếu của B lên cạnh CD. Biết ABED là hình vuông và diện tích hình thang ABCD gấp 2 lần diện tích hình vuông ABED. Hãy tính khoảng cách từ C đến đường thẳng BE.
Bài 5: Cho tam giác ABC cân tại A. Có M là trung điểm của đoạn thẳng BC. Chứng minh AM là khoảng cách từ A đến cạnh BC của tam giác ABC.







