Hai tam giác bằng nhau lớp 7
Chuyên đề Toán học lớp 7: Hai tam giác bằng nhau được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Hai tam giác bằng nhau
A. Lý thuyết
1. Định nghĩa
Hai tam giác ABC và A'B'C' bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
2. Kí hiệu
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A'B'C' ta viết Δ ABC = Δ A'B'C'
Người ta quy ước rằng khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự.
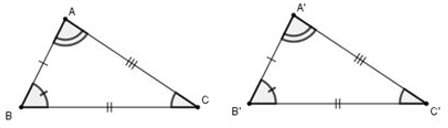
Ví dụ:
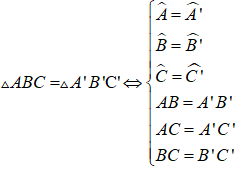
Trong đó A, A' là hai đỉnh tương ứng, AB, A'B' là hai cạnh tương ứng, ∠A, ∠A' là hai góc tương ứng.
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho Δ ABC = Δ MNP. Chọn đáp án sai
A. AB = MN
B. AC = NP
C. 
\(\widehat{M} =\widehat{A}\)
D. \(\widehat{P} =\widehat{C}\)
Trả lời:
Ta có: Δ ABC = Δ MNP ⇒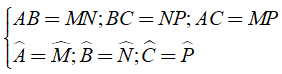
Vậy đáp án B sai.
Chọn đáp án B.
Bài 2: Cho Δ ABC = Δ DEF. Biết \(\widehat{A} =33^{\circ}\), khi đó:
A. \(\widehat{D} =33^{\circ}\)
B. \(\widehat{D} =42^{\circ}\)
C. \(\widehat{E} =32^{\circ}\)
D. \(\widehat{D} =66^{\circ}\)
Trả lời:
Ta có: Δ ABC = Δ DEF ⇒ \(\widehat{A} =\widehat{D}=33^{\circ}\)
Chọn đáp án A.
Bài 3: Cho hai tam giác ABC và DEF có: AB = EF, BC = FD, AC = ED; \(\widehat{A} =\widehat{E}\), \(\widehat{B} =\widehat{F}\), \(\widehat{D} =\widehat{C}\). Khi đó
A. Δ ABC = Δ DEF
B. Δ ABC = Δ EFD
C. Δ ABC = Δ FDE
D. Δ ABC = Δ DFE
Trả lời:
Xét hai tam giác ABC và DEF có: AB = EF, BC = FD, AC = ED; \(\widehat{A} =\widehat{E}\), \(\widehat{B} =\widehat{F}\), \(\widehat{D} =\widehat{C}\)
Nên Δ ABC = Δ EFD
Chọn đáp án B.
Bài 4: Cho Δ ABC = Δ DEF, Biết \(\widehat{A} =32^{\circ}\), \(\widehat{F} =78^{\circ}\). Tính \(\widehat{B} ,\widehat{E}\)
A. \(\widehat{B} =\widehat{E} =60^{\circ}\)
B. \(\widehat{B} = 60^{\circ};\ \widehat{E} =70^{\circ}\)
C. \(\widehat{B} =\widehat{E} =78^{\circ}\)
D. \(\widehat{B} =\widehat{E} =70^{\circ}\)
Trả lời:
Vì Δ ABC = Δ DEF nên \(\widehat{A} =\widehat{D}=32^{\circ}\); \(\widehat{B} =\widehat{E}\); \(\widehat{C} =\widehat{F}=78^{\circ}\)
Xét tam giác ABC có: \(\widehat{A} +\widehat{B}+\widehat{C} =180^{\circ}\)
⇒ \(\widehat{B} =180^{\circ} -(\widehat{A}+\widehat{C})=180^{\circ} -(32^{\circ} +78^{\circ} )=70^{\circ}\)
Vậy \(\widehat{B}=\widehat{E}=70^{\circ}\)
Chọn đáp án D
Bài 5: Cho Δ ABC = Δ MNP. Biết AB = 5 cm, MP = 7 cm và chu vi của tam giác ABC bằng 22 cm. Tính các cạnh còn lại của mỗi tam giác?
A. NP = BC = 9 cm
B. NP = BC = 11 cm
C. NP = BC = 10 cm
D. NP = 9 cm; BC = 10 cm
Lời giải:
Vì Δ ABC = Δ MNP nên AB = MN = 5 cm; BC = NP; AC = MP = 7 cm
Chu vi tam giác ABC: AB + AC + BC = 22
⇒ BC = 22 – (AB + AC) = 22 – 12 = 10 (cm)
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Cho tam giác ABC có chu vi bằng 21 cm. Độ dài là ba số lẻ liên tiếp và AB < BC < AC. Tìm độ dài các cạnh của tam giác PQR biết tam giác ABC bằng tam giác PQR.
Gọi độ dài cạnh AB là 2n – 1 thì độ dài cạnh BC là 2n + 1 và độ dài cạnh AC là 2n + 3
Theo bài ra ta có: AB + BC + AC = 21 ⇒ (2n – 1) + (2n + 1) + (2n + 3) = 21
⇒ 6n = 18 ⇔ n = 3
Do đó, ta có: AB = 5 cm, BC = 7 cm, AC = 9 cm
Theo giả thiết ta lại có: Δ ABC = Δ PQR nên AB = PQ = 5 cm, BC = QR = 7 cm, AC = PR = 9 cm
Vậy PQ = 5 cm, QR = 7 cm, PR = 9 cm
Bài 2: Cho tam giác ABC có M thuộc cạnh BC sao cho Δ AMB = Δ AMC. Chứng minh rằng:
a) M là trung điểm của BC
b) AM là tia phân giác của góc A
c) AM ⊥ BC
a) Vì Δ AMB = Δ AMC nên ta có: MB = MC
Mà M nằm giữa B và C
⇒ M là trung điểm của cạnh BC
b) Vì Δ AMB = Δ AMC nên \(\widehat{AMB}=\widehat{AMC}\)
Mà \(\widehat{MAB}+\widehat{MAC}=\widehat{A} \Rightarrow \widehat{MAB}=\widehat{MAC}=\frac{1}{2} \widehat{BAC}\)
Mặt khác: tia AM nằm giữa hai tia AB và AC nên tia AM là tia phân giác của góc ∠BAC
c) Vì Δ AMB = Δ AMC nên ta có: \(\widehat{AMB}=\widehat{AMC}\)
Mà M thuộc tia BC nên \(\widehat{AMB}+\widehat{AMC}=180^{\circ} \Rightarrow \widehat{AMB}=\widehat{AMC}=90^{\circ}\)
Hay AM ⊥ BC (đpcm)
Bài 3: Cho Δ ABC = Δ IHK. Tính chu vi của mỗi tam giác, biết rằng AB = 6 cm, AC = 8 cm, HK = 12 cm.
Lời giải:
Vì Δ ABC = Δ IHK nên AB = IH = 6 cm, BC = HK = 12 cm, AC = IK = 8 cm (các cạnh tương ứng).
Chu vi của mỗi tam giác là: 6 cm + 12 cm + 8 cm = 26 cm.
Bài 4: Cho Δ ABC = Δ MNP. Biết AB + BC = 7 cm, MN - NP = 3 cm, MP = 4 cm. Tính độ dài các cạnh của mỗi tam giác.
Lời giải:
Vì Δ ABC = Δ MNP nên AB = MN, BC = NP, AC = MP (các cạnh tương ứng)
Mà MP = 4 cm nên AC = 4 cm
MN - NP = 3 cm hay AB - BC = 3 cm
Do đó AB = (7 + 3) : 2 = 5 cm; BC = AB - 3 = 2 cm
Vậy Δ ABC có: AB = 5 cm; AC = 4 cm; BC = 2 cm
Δ MNP có: MN = 5 cm; MP = 4 cm; NP = 2 cm
-----------------------
