Tính chất ba đường phân giác của tam giác
Tính chất ba đường phân giác của tam giác là nội dung được học trong chương trình Toán 7. Đây là phần nội dung quan trọng, thường xuất hiện trong các bài kiểm tra Toán 7. Để giúp các em nắm vững phần này, VnDoc gửi tới các bạn tài liệu Chuyên đề Toán học lớp 7: Tính chất ba đường phân giác của tam giác. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Tính chất ba đường phân giác của tam giác
A. Lý thuyết Tính chất ba đường phân giác của tam giác
1. Đường phân giác của tam giác
• Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm M, khi đó đoạn thẳng AM được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC. Ta cũng gọi đường thẳng AM là đường phân giác của tam giác ABC.
• Mỗi tam giác có ba đường phân giác.
Tính chất: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến ứng với cạnh đáy.
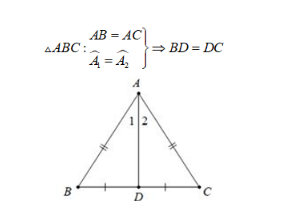
2. Tính chất ba đường phân giác của tam giác
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Tam giác ABC có ba đường phân giác giao nhau tại I, khi đó:
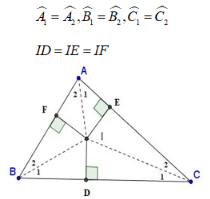
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho ΔABC có ∠A = 90°, các tia phân giác của ∠B và ∠C cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh AB và AC. Khi đó ta có:
A. AI là đường cao của ΔABC
B. IA = IB = IC
C. AI là đường trung tuyến của ΔABC
D. ID = IE
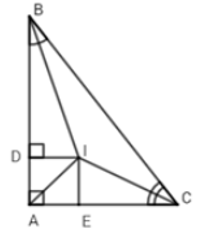
Xét ΔABC có các tia phân giác của ∠B và ∠C cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔABC, suy ra AI là đường phân giác của góc ∠A và I cách đều ba cạnh của ΔABC (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A,B và C
Vì I là giao điểm của ba đường phân giác trong ΔABC nên ⇒ DI = IE (tính chất 3 đường phân giác của tam giác)
Chọn đáp án D
Bài 2: Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có
A. I cách đều ba đỉnh của ΔABC
B. A, I, G thẳng hàng
C. G cách đều ba cạnh của ΔABC
D. Cả 3 đáp án trên đều đúng
Lời giải:
I là giao điểm của các đường phân giác trong tam giác nên I cách đều ba cạnh của ΔABC . Loại đáp án A
Ta có: ΔABC cân tại A, I là giao điểm của các đường phân giác trong tam giác nên AI vừa là đường trung tuyến đồng thời là đường phân giác của ∠BAC. Mà G là trọng tâm của tam giác ΔABC nên A, I, G thẳng hàng. Chọn B
Chọn đáp án B
Bài 3: Cho ΔABC cân tại A, trung tuyến AM. Gọi D là một điểm nằm giữa A và M. Khi đó ΔBDC là tam giác gì?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Tam giác vuông cân
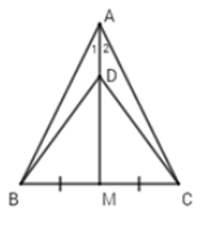
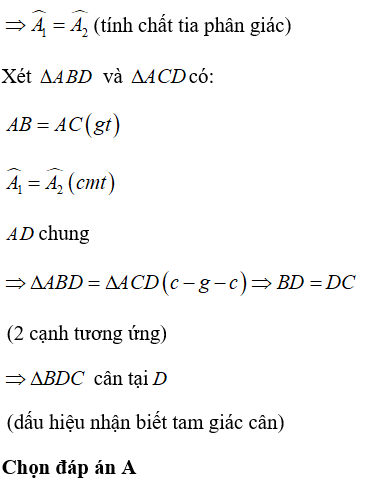
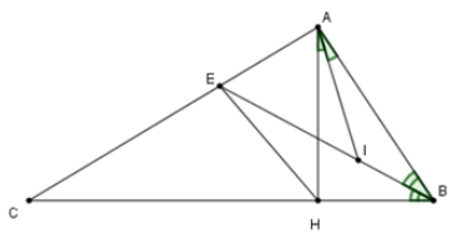
Bài 4: Cho ΔABC có AH ⊥ BC và 
\(\widehat{BAH} =2\widehat{C}\). Tia phân giác của góc B cắt AC tại E. Tia phân giác của góc BAH cắt BE ở I. Khi đó tam giác AIE là tam giác
A. Vuông cân tại I
B. Vuông cân tại E
C. Vuông cân tại A
D. Cân tại I
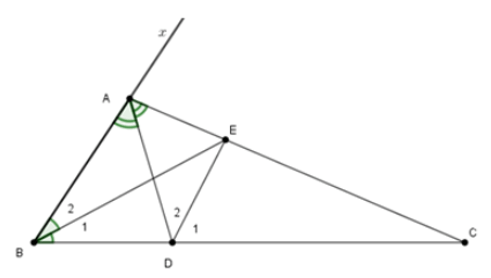
Bài 5: Cho ΔABC có ∠A = 120°. Các đường phân giác AD, BE . Tính số đo góc BED
A. 55°
B. 45°
C. 60°
D. 30°
II. Bài tập tự luận
Bài 1: Hai đường phân giác của góc B và góc C cắt nhau tại I. Chứng minh rằng
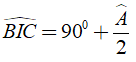
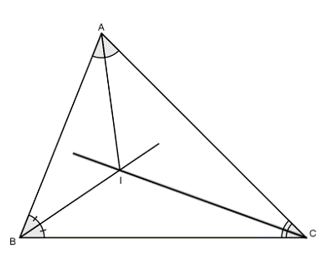
I là giao điểm của hai đường phân giác góc B và góc C
⇒ Phân giác góc A là AI.
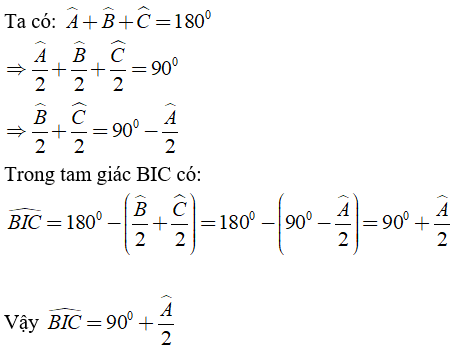
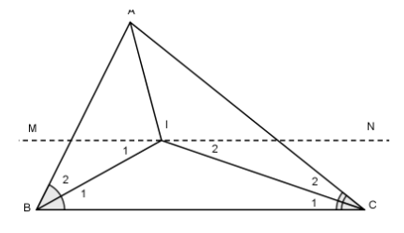
Bài 2: Cho ΔABC Gọi I là giao điểm của hai tia phân giác góc A và góc B. Qua I kẻ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Chứng minh rằng MN = BM + CN
Ba phân giác của một tam giác cùng đi qua một điểm nên CI là tia phân giác của góc C
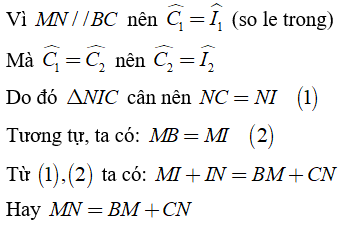
C. Bài tập tự luyện
Bài 1: Cho điểm M nằm trên tia phân giác At của góc xAy nhọn. Kẻ MH ⊥ Ax ở H và MK ⊥ Ay ở K.
a) So sánh MH và MK.
b) Chứng minh:
Bài 2: Cho tam giác ABC, có trung tuyến AM cũng là đường phân giác. Kẻ ở H và ở K.
a) So sánh MH và MK.
b) Chứng minh: Δ AMH = Δ AKM
c) Tam giác ABC là tam giác gì?
Bài 3: Cho tam giác ABC cân tại A có hai đường phân giác BD và CE cắt nhau tại H. đường thẳng AH cắt BC ở M.
a) Đường thẳng AM là đường đặt biệt gì của tam giác ABC.
b) So sánh Δ ABM và Δ ACM.
c) Tính số đo góc AMB.
Bài 4: Cho tam giác ABC cân tại A có AM là đường trung tuyến.
a) So sánh góc BAM và góc CAM.
b) Lấy điểm D trên AM. Kẻ DH ⊥ AB ở H và DK ⊥ AC ở K. Chứng minh: Δ DHK cân.
Bài 5: Cho tam giác ABC cân tại A. Kẻ các tia phân giác BD, CE. Lấy M là trung điểm của BC.
a) Chứng minh AM là tia phân giác của góc BAC.
b) Ba đường thẳng AM, BD, CE đồng quy.
Bài 6: Cho tam giác ABC, tia phân giác AD. Các tia phân giác ngoài tại đỉnh B và C cắt nhau ở E. Chứng minh ba điểm A, D, E thẳng hàng.
Bài 7: Cho tam giác ABC. Phân giác trong của góc B và góc C cắt nhau tại I. Phân giác các góc ngoài tại đỉnh B và đỉnh C cắt nhau tại J, phân giác các góc ngoài tại đỉnh A và đỉnh C cắt nhau tại K, phân giác các góc ngoài tại đỉnh A và đỉnh B cắt nhau tại L.
a) Chứng minh \(\widehat{BIC} =90^{\circ} +\frac{\widehat{A}}{2}\)
b) Chứng minh ba điểm A, I, J thẳng hàng
c) Chứng minh AJ, BK, CL cắt nhau tại một điểm.
