Cộng, trừ đa thức
Chuyên đề Toán học lớp 7: Cộng, trừ đa thức được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Cộng, trừ đa thức
Ngoài ra các bạn có thể xem thêm các tài liệu như Trắc nghiệm về Cộng, trừ Đa thức hay bài tập về cộng, trừ đa thức để ngoài giải các bài tập trong sách giáo khoa, sách bài tập hay chuyên đề Toán lớp 7 này có thể tham khảo thêm các tài liệu phía trên nhằm củng cố, luyện tập và nâng cao các kiến thức đã được học trong chương 4: Biểu thức đại số này.
Tham khảo thêm:
A. Lý thuyết
Để cộng (hay trừ) hai đa thức, ta làm như sau:
• Bước 1: Viết hai đa thức trong dấu ngoặc.
• Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc).
• Bước 3: Nhóm các hạng tử đồng dạng.
• Bước 4: Cộng, trừ các đơn thức đồng dạng.
Ví dụ 1: Cộng hai đa thức M = 5x2y + 5x + 3 và N = xyz - 4x2y + 5x - 1/2
Ta có: 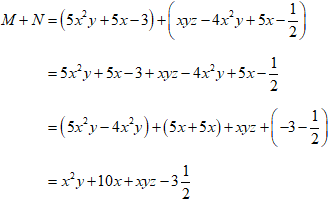
Ví dụ 2: Trừ hai đa thức P = 5x2y - 4xy2 + 5x - 3 và Q = xyz - 4x2y + xy2 + 5x - 1/2
Ta có:
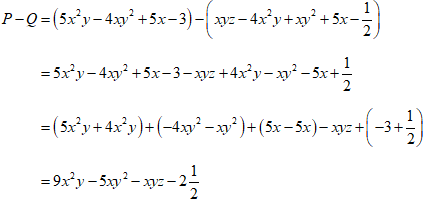
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Thu gọn đa thức 3y(x2 - xy) - 7x2(y + xy) ta được
A. -4x2y - 3xy2 + 7x3y
B. -4x2y - 3xy2 - 7x3y
C. 4x2y + 3xy2 - 7x3y
D. 4x2y + 3xy2 + 7x3y
Ta có 3y(x2 - xy) - 7x2(y + xy) = 3x2y - 3xy2 - 7x2y - 7x3y
= (3x2y - 7x2y) - 3xy2 - 7x3y = -4x2y - 3xy2 - 7x3y
Chọn đáp án B
Bài 2: Đa thức (1/5)xy(x + y) - 2(x2y - xy2) có bậc là:

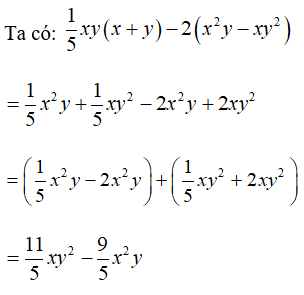
Chọn đáp án D
Bài 3: Đa thức nào dưới đây là kêt quả của phép tính 4x3yz - 4xy2z2 - yz(xyz + x3) ?
A. 3x3yz - 5xy2z2
B. 3x3yz + 5xy2z2
C. -3x3yz - 5xy2z2
D. 5x3yz - 5xy2z2
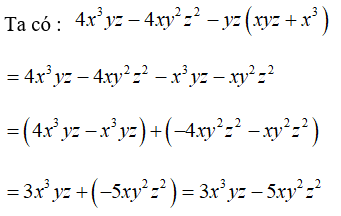
Chọn đáp án A
Bài 4: Cho các đa thức A = 4x2 - 5xy + 3y2; B = 3x2 + 2xy + y2; C = -x2 + 3xy + 2y2. Tính A + B + C
A. 7x2 + 6y2 B. 5x2 + 5y2 C. 6x2 + 6y2 D. 6x2 - 6y2
Ta có

Chọn đáp án C
Bài 5: Cho các đa thức A = 4x2 - 5xy + 3y2; B = 3x2 + 2xy + y2; C = -x2 + 3xy + 2y2. Tính A - B - C
A. -10x2 + 2xy B. -2x2 - 10xy C. 2x2 + 10xy D. 2x2 - 10xy
Ta có

Chọn đáp án D
Bài 6: Cho các đa thức A = 4x2 - 5xy + 3y2; B = 3x2 + 2xy + y2; C = -x2 + 3xy + 2y2. Tính C - A - B
A. 8x2 + 6xy + 2y2 B. -8x2 + 6xy - 2y2
C. 8x2 - 6xy - 2y2 D. 8x2 - 6xy + 2y2
Ta có
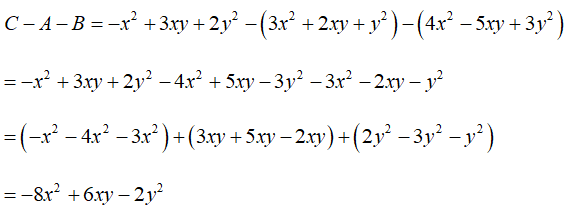
Chọn đáp án B
II. Bài tập tự luận
Bài 1: Tìm đa thức M biết
a) M - (2x3 - 4xy + 6y2) = x2 + 3xy - y2
b) (2x2 - 4xy + y2) + M = 0
c) (2x2 -7xy + 3y2) - 2M = 4x2 - 5xy + 9y2

Bài 2: Tính giá trị của các đa thức sau
a) 2x3 + y2 + 2xy - 3y3 + 2x3 + 3y3 - 3x3 tại x = 4; y = 5
b) x6y6 - x4y4 + x2y - xy + 1 tại x = 1; y = -1
a) Ta có : 2x3 + y2 + 2xy - 3y3 + 2x3 + 3y3 - 3x3
= (2x3 + 2x3 - 3x3) + y2 + 2xy + (-3y3 + 3y2)
= x3 + y2 + 2xy
Tại x = 4, y = 5, ta có:
43 + 52 + 2.4.5 = 64 + 25 + 40 = 129
b) Ta có: x6y6 - x4y4 + x2y - xy + 1
Tại x = 1, y = -1 ta có:
(1)6.(-1)6 - (1)4.(-1)4 + (1)2.(-1) - 1.(-1) + 1 = 1 - 1 - 1 + 1 + 1 = 1
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 7: Cộng, trừ đa thức. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc







