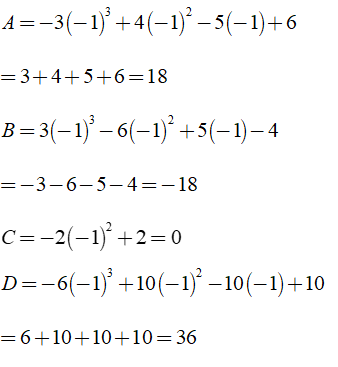Cộng, trừ đa thức một biến
Chuyên đề: Cộng, trừ đa thức một biến
Cộng, trừ đa thức một biến là phần nội dung quan trọng trong chương trình Toán 7. Để giúp các em nắm vững kiến thức phần này, VnDoc gửi tới các bạn Chuyên đề Toán học lớp 7: Cộng, trừ đa thức một biến. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hơn. Mời các bạn tham khảo.
A. Lý thuyết Cộng trừ đa thức một biến
Để cộng (hay trừ) các đa thức một biến, ta làm một trong hai cách sau:
• Cách 1: Cộng, trừ đa thức theo “hàng ngang”
• Cách 2: Sắp xếp các hạng từ của hai đa thức cùng theo lũy thừa giảm (hoặc tăng) của biến rồi đặt phép tính theo cột dọc tương ứng như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột)
Ví dụ: Cho hai đa thức P(x) = x5 - 2x4 + x2 - x + 1; Q(x) = 6 - 2x + 3x3 + x4 - 3x5. Tính P(x) - Q(x).
P(x) - Q(x) = (x5 - 2x4 + x2 - x + 1) - (6 - 2x + 3x3 + x4 - 3x5)
= x5 - 2x4 + x2 - x + 1 - 6 + 2x - 3x3 - x4 + 3x5
= 4x5 - 3x4 - 3x3 + x2 + x5
B. Trắc nghiệm & Tự luận Cộng trừ đa thức một biến
I. Câu hỏi trắc nghiệm
Bài 1: Tìm hai đa thức P(x) và Q(x) sao cho P(x) + Q(x) = x2 + 1
A. P(x) = x2; Q(x) = x + 1
B. P(x) = x2 + x; Q(x) = x + 1
C. P(x) = x2; Q(x) = -x + 1
D. P(x) = x2 - x; Q(x) = x + 1
Ta có với P(x) = x2 - x; Q(x) = x + 1
P(x) + Q(x) = x2 - x + x + 1 = x2 + 1
Chọn đáp án D
Bài 2: Cho f(x) = x5 - 3x4 + x2 - 5 và g(x) = 2x4 + 7x3 - x2 + 6. Tìm hiệu f(x) - g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
A. 11 + 2x2 + 7x3 - 5x4 + x5
B. -11 + 2x2 - 7x3 - 5x4 + x5
C. x5 - 5x4 - 7x3 + 2x2 - 11
D. x5 - 5x4 - 7x3 + 2x2 + 11
Ta có
Sắp xếp theo lũy thừa tăng dần của biến ta được
-11 + 2x2 - 7x3 - 5x4 + x5
Chọn đáp án B
Bài 3: Cho p(x) = 5x4 + 4x3 - 3x2 + 2x - 1 và q(x) = -x4 + 2x3 - 3x2 + 4x - 5
Tính p(x) + q(x) rồi tìm bậc của đa thức thu được
A. p(x) + q(x) = 6x3 - 6x2 + 6x - 6 có bậc là 6
B p(x) + q(x) = 4x4 + 6x3 - 6x2 + 6x + 6 có bậc là 4
C. p(x) + q(x) = 4x4 + 6x3 - 6x2 + 6x - 6 có bậc là 4
D. P(x) + q(x) = 4x4 + 6x3 + 6x - 6 có bậc là 4
Ta có p(x) + q(x)
Bậc của đa thức p(x) + q(x) = 4x4 + 6x3 - 6x2 + 6x - 6 có bậc là 4
Chọn đáp án C
Bài 4: Tìm đa thức h(x) biết f(x) - h(x) = g(x) biết
f(x) = x2 + x + 1; g(x) = 4 - 2x3 + x4 + 7x5
A. h(x) = -7x5 - x4 + 2x3 + x2 + x - 3
B. h(x) = 7x5 - x4 + 2x3 + x2 + x + 3
C. h(x) = -7x5 - x4 + 2x3 + x2 + x + 3
D. h(x) = 7x5 + x4 + 2x3 + x2 + x + 3
Ta có f(x) - h(x) = g(x) ⇒ h(x) = f(x) - g(x)
Mà f(x) = x2 + x + 1; g(x) = 4 - 2x3 + x4 + 7x5 nên h(x) = x2 + x + 1 - (4 - 2x3 + x4 + 7x5)
= x2 + x + 1 - 4 + 2x3 - x4 - 7x5
Vậy h(x) = -7x5 - x4 + 2x3 + x2 + x - 3
Chọn đáp án A
Bài 5: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = x4 - 4x2 + 6x3 + 2x - 1; g(x) = x + 3
A. -1 B. 1 C. 4 D. 6
Ta có f(x) + k(x) = g(x) ⇒ k(x) = g(x) - f(x)
= x + 3 - (x4 - 4x2 + 6x3 + 2x - 1)
= x + 3 - x4 + 4x2 - 6x3 - 2x + 1 = -x4 - 6x3 + 4x2 - x + 4
Nhận thấy số hạng có lũy thừa cao nhất của biến là -x4 nên hệ số cao nhất là -1
Chọn đáp án A
Bài 6: Tìm hệ số tự do của hiệu f(x) - 2.g(x) với
f(x) = 5x4 + 4x3 - 3x2 + 2x - 1; g(x) = -x4 + 2x3 - 3x2 + 4x + 5
A. 7 B. 11 C. -11 D. 4
- Ta có:
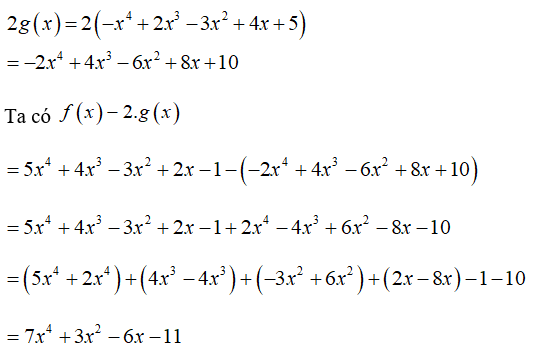
Hệ số cần tìm là -11
Chọn đáp án C
II. Bài tập tự luận
Bài 1: Cho đa thức P(x) = -9x3 + 5x4 + 8x2 - 15x3 - 4x2 - x4 + 15 - 7x3
Tính P(1), P(0), P(-1)
Trước hết ta thu gọn đa thức:
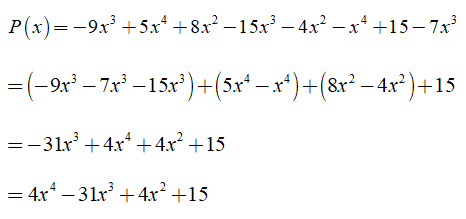
Khi đó ta có:
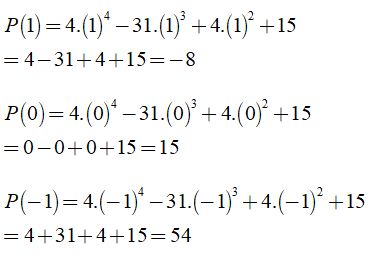
Bài 2: Cho đa thức
A = -3x3 + 4x2 - 5x + 6
B = 3x3 - 6x2 + 5x - 4
a) Tính C = A + B, D = A - B, E = C - D
b) Tính các giá trị của đa thức A, B, C, D tại x = -1
a) Ta có:
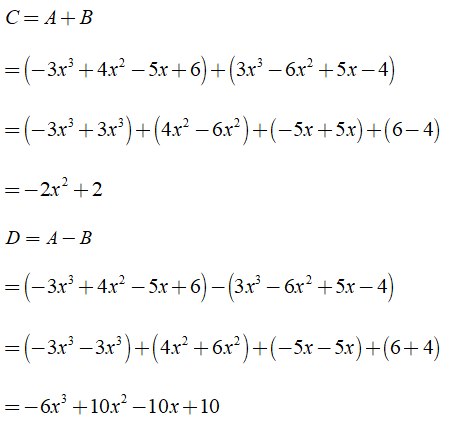
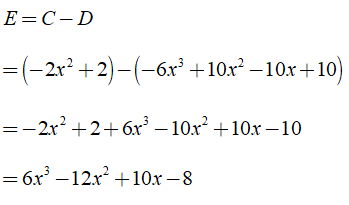
b) Tính giá trị biểu thức tại x = -1
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 7 Cộng, trừ đa thức một biến. Ngoài ra các bạn có thể xem thêm các tài liệu như Trắc nghiệm về cộng, trừ đa thức một biến hay bài tập về cộng, trừ đa thức một biến để củng cố, luyện tập và nâng cao các kiến thức đã được học về Biểu thức đại số lớp 7.
Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc .
