Hai đường thẳng song song
Chuyên đề Toán học lớp 7: Hai đường thẳng song song được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Hai đường thẳng song song
A. Lý thuyết
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
– Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A, bốn góc đỉnh B. Mỗi cặp gồm một góc đỉnh A và một góc đỉnh B.
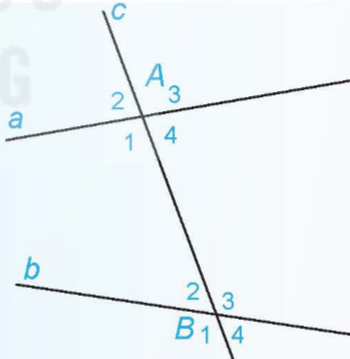
• Các cặp góc A1 và B3, A4 và B2 được gọi là các cặp góc so le trong.
• Các cặp góc A1 và B1, A2 và B2, A3 và B3, A4 và B4 được gọi là các cặp góc đồng vị.
– Tính chất: Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
• Hai góc so le trong còn lại bằng nhau
• Hai góc đồng vị bằng nhau
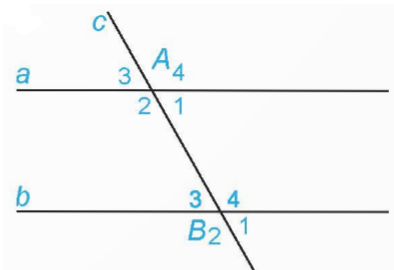
2. Định nghĩa hai đường thẳng song song
– Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung
3. Dấu hiệu nhận biết hai đường thẳng song song
– Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song
– Nếu hai đường thẳng cắt một đường thẳng thứ ba tao thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song
– Nhận xét: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
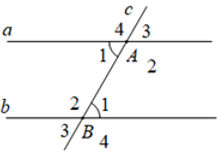
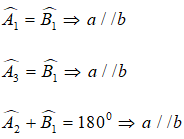
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Chọn câu trả lời đúng trong các câu sau:
A. Hai đường thẳng không có điểm chung thì song song với nhau
B. Hai đoạn thẳng có điểm chung thì song song với nhau
C. Hai đường thẳng phân biệt không cắt nhau thì song song với nhau
D. Hai đường thẳng song song là hai đường thẳng không trùng nhau
Giải thích: Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn đáp án A.
Bài 2: Chọn câu đúng nhất:
A. Nếu hai đường thẳng cắt đường thẳng tạo thành một cặp góc so le trong bằng nhau thì //
B. Nếu hai đường thẳng cắt đường thẳng tạo thành một cặp góc đồng vị bằng nhau thì //
C. Hai đường thẳng cắt đường thẳng và trong các góc tạo thành có mọt cặp góc so le ngoài bằng nhau thì //
D. Cả A, B, C đều đúng
Giải thích:
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
Nên cả A, B, C đều đúng.
Chọn đáp án D.
Bài 3: Điền vào chỗ trống: “Nếu hai đường thẳng d, d' cắt đường thẳng xy tạo thành một cặp góc trong cùng phía … thì d // d' ”
A. Bù nhau
B. Bằng nhau
C. Phụ nhau
D. Kề nhau
Giải thích: Nếu hai đường thẳng cắt đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
Chọn đáp án A.
II. Bài tập tự luận
Bài 1: Cho ∠xOy = α, điểm A nằm trên tia Oy. Qua A vẽ tia Am. Tính số đo góc OAm để AM song song với Ox.
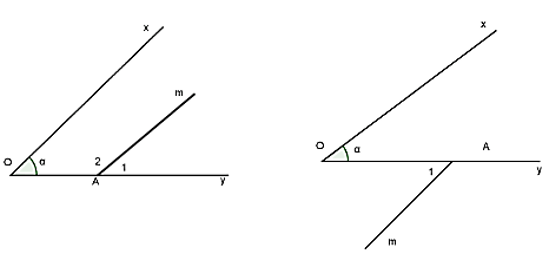
Xét hai trường hợp:
a) Nếu tia Am thuộc miền trong góc xOy
Bài 2: Cho đường thẳng a và b cắt đường thẳng c tại A và B. Cho biết tổng của hai góc trong cùng phía với một góc so le trong với một trong hai góc này bằng 300° và trong hai góc kề bù có góc này bằng gấp đôi góc kia. Hai đường thẳng a và đường thẳng b có song song với nhau không? Vì sao?
Bài 3: Cho hình vẽ bên dưới.
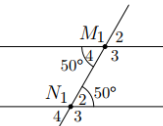
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Ghi tiếp số đo ứng với các góc còn lại.
- Tổng ba góc của một tam giác
- Tổng ba góc của một tam giác
- Hai tam giác bằng nhau
- Hai tam giác bằng nhau
- Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c)
- Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
- Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
- Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
- Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g)
- Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
- Tam giác cân
- Tam giác cân
- Định lí Pi-ta-go
- Định lí Pi-ta-go
- Các trường hợp bằng nhau của tam giác vuông
- Các trường hợp bằng nhau của tam giác vuông
