Đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) Đề 1

Bộ đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 1 được biên soạn bám sát nội dung chương trình SGK Cánh Diều mới nhất, giúp học sinh lớp 9 củng cố kiến thức trọng tâm trước kỳ thi. Đề thi bao gồm các dạng bài quen thuộc như hàm số bậc nhất, hệ phương trình, đường tròn,… cùng đáp án chi tiết và hướng dẫn giải rõ ràng, giúp học sinh dễ dàng tự ôn tập, kiểm tra năng lực và làm quen với cấu trúc đề thi mới của Bộ GD&ĐT.
Tài liệu là nguồn tham khảo hữu ích cho giáo viên, phụ huynh và học sinh lớp 9, góp phần nâng cao hiệu quả học tập và chuẩn bị tốt cho các kỳ kiểm tra định kỳ.

Họ và tên học sinh: ………………………… Lớp: ………………………

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Phương trình nào sau đây là phương trình tích?

A. \((x - 3)(3x + 1) = 2\).                                  B. \((x - 3)(2x + 3) = (x - 3)\).

C. \((x - 3)(2x + 3) = (x - 3)\).                        D. \((x - 5)(x + 1) = 0\).

Câu 2. Điều kiện xác định của phương trình \(\frac{1 - 2x}{x^{2}} = \frac{1}{2}\) là: 

A. \(x \neq \frac{1}{2}\).           B. \(x \neq 0\).              C. \(x \neq 2\).              D. \(x \neq \frac{1}{2}\) và \(x \neq 0\).

Câu 3: Chu vi một mảnh vườn hình chữ nhật là \(30m\). Biết chiều dài hơn chiều rộng \(5\ m\). Tính diện tích hình chữ nhật.

A. \(100\ m^{2}\).                   B. \(70\ m^{2}\).                      C. \(50\ m^{2}\).                      D. \(55\ m^{2}\).

Câu 4: Phương trình \(- 2x - y = 4\) tương đương với phương trình nào sau đây?

A. \(2x + y = 4\)               B.\(2x = 4 + y\)                   C. \(y = - 2x - 4\)             D. \(x = 2 + \frac{y}{2}\)

Câu 5: Cho bất đẳng thức \(2 \geq 3a - 1\). Bất đẳng thức nào cùng chiều với bất đẳng thức đã cho

A. \(4 < 2a\).                   B. \(3a - 2 \leq 4\).               C. \(2 = 3a - 1\).                   D. \(a - 1 \geq - 2\).

Câu 6: Trong các số \(- 3;\ \ 4;\ \ 0;\ \ 2\) số nào là nghiệm của bất phương trình \(3x - 7 \geq 0\)

A. \(- 3\).                           B. \(4\).               C. \(0\).               D. \(2\).

Câu 7: Cho hệ phương trình \(\left\{ \begin{matrix} 2x + y = 3\ \ \ (1) \\ 4x + 3y = 7\ \ (2) \end{matrix} \right.\). Dùng quy tắc thế để tạo ra phương trình mới. Hãy chọn cách biến đổi chính xác nhất?

A. Chọn phương trình (1) và biểu thị y theo x ta được \(y = 3 + 2x\).

B. Chọn phương trình (1) và biểu thị y theo x ta được \(y = 3 - 2x\).

C. Chọn phương trình (1) và biểu thị y theo x ta được \(y = 2x - 3\).

D. Chọn phương trình (1) và biểu thị y theo x ta được \(y = - 3 - 2x\).

Câu 8: Nếu tam giác \(ABC\) có \(\widehat{A} = 90^{0};AB = 3cm;BC = 5cm\). Tính giá trị \(\sin\widehat{C}\)?

A. \(\frac{5}{3}\)               B. \(\frac{3}{5}\)                  C. \(\frac{4}{5}\)                     D. \(\frac{3}{4}\)

Câu 9: Cho hình vẽ:

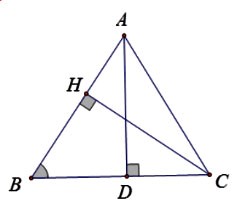
Chọn hệ thức đúng?

A. \(HC = BC.sin\widehat{B}\)                             B. \(HC = BC.cos\widehat{B}\)

C. \(HC = BC.tan\widehat{B}\)                          D. \(HC = BC.cot\widehat{B}\)

Câu 10: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat{B} = 60^{0}\) và \(AB = \sqrt{3}cm\). Khi đó độ dài cạnh \(AC\) là:

A. \(AC = \sqrt{3}cm\)                                B. \(AC = \frac{3\sqrt{3}}{2}cm\)

C. \(AC = 2\sqrt{3}cm\)                              D. \(AC = 3cm\)

Câu 11: Cho hình vẽ:

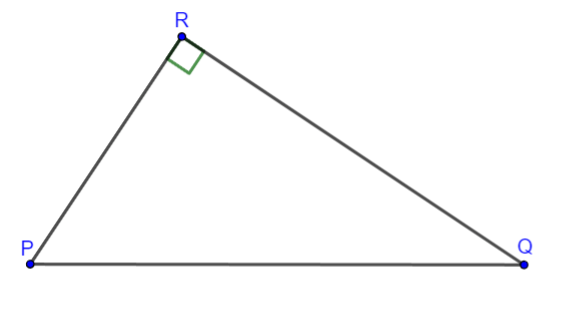
Chọn khẳng định đúng?

A. \(\sin\widehat{Q} = \frac{PR}{QR}\)              B. \(\sin\widehat{Q} = \frac{QR}{PR}\)                   C. \(\sin\widehat{Q} = \frac{QR}{PQ}\)               D. \(\sin\widehat{Q} = \frac{PR}{PQ}\)

Câu 12: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat{B} = 35^{0};a = 20\). Tính giá trị của \(b\)?

A. \(b = 28,56\)                    B. \(b = 11,47\)                 C. \(b = 14\)                              D. \(b = 16,38\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Chiều cao của các bạn nam trong lớp 9A từ \(1,5m\) đến \(1,8m\).

a) Bạn An là học sinh nam lớp 9A và có chiều cao \(h > 1,8m\).

b) Bạn My là bạn nữ lớp 9A và có chiều cao \(h > 1,5m\).

c) Chiều cao \(h\) của các bạn nam trong lớp 9A được biểu diễn là \(1,5 \leq h < 1,8\).

d) Chiều cao \(h\) của các bạn nam trong lớp 9A được biểu diễn là \(1,5 \leq h \leq 1,8\).

Câu 2: Cho hệ phương trình \(\left\{ \begin{matrix} 2x + 3y = 7\ \ \ (1) \\ 5x - 2y = 8\ \ \ (2) \end{matrix} \right.\).

a) Biên đổi \(x\) theo \(y\) thì phương trình \((1)\) viết lại thành \(y = \frac{7}{3} - \frac{2}{3}x\).

b) Biến đổi \(y\) theo \(x\) thì phương trình \((2)\) viết lại thành \(x = \frac{2}{5}y + \frac{8}{5}\)

c) Nhân cả hai vế của phương trình \((1)\) với \(2\)và nhân cả hai vế của phương trình \((2)\) với \(3\) ta được hệ phương trình sau: \(\left\{ \begin{matrix} 4x + 6y = 14 \\ 15x - 6y = 24 \end{matrix} \right.\).

d) Biến đổi phương trình \((1)\) với \(x\) theo \(y\), rồi thay vào phương trình \((2)\) ta được \(y = - 1\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình và bất phương trình sau:

a) \(\left( \dfrac{2}{3}x + 6 \right)(8 -2x) = 0.\)                             b) \(3(x - 2) - 5 \geq 3(2x - 1).\)

Câu 2: Giải bài toán sau bằng cách lập hệ phương trình:

Một chiếc thuyền xuôi dòng và ngược dòng trên khúc sông dài \(40\) km hết \(4\) giờ \(30\) phút. Biết thời gian thuyền xuôi dòng \(5\) km bằng thời gian thuyền ngược dòng \(4\) km. Tính vận tốc dòng nước.

Câu 3: 3.1) Rút gọn các biểu thức sau:

a) \(A = sin35{^\circ} + sin67{^\circ} - cos23{^\circ} - cos55{^\circ}.\)        b) \(B= cot20{^\circ} \cdot cot40{^0} \cdot cot50{^\circ} \cdot \cot70{^0}.\)

3.2) Một cầu trượt có độ dốc là \(28^{0}\) và có độ cao là \(2,1m\). Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).

Câu 4: Trong mùa cao điểm du lịch, một tổ hợp nhà nghỉ ở Đà Nẵng gồm \(100\) phòng đồng giá luôn luôn kín phòng khi giá thuê là \(480\) nghìn đồng/phòng. Qua khảo sát các năm trước bộ phận kinh doanh của nhà nghỉ thấy rằng: cứ tăng giá phòng lên \(x\%\) \((x \geq 0)\)so với lúc kín phòng (giá thuê là \(480\) nghìn đồng/phòng) thì số phòng cho thuê giảm đi \(\frac{4x}{5}\%\). Hỏi nhà nghỉ phải niêm yết giá phòng là bao nhiêu để đạt doanh thu cao nhất?

------------------- Hết ----------------------

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

Với đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 1 có đáp án chi tiết, học sinh sẽ nắm vững kiến thức cốt lõi, rèn kỹ năng trình bày bài toán và tự tin bước vào kỳ thi giữa học kì. Hãy tiếp tục luyện tập thêm các đề thi Toán 9 Cánh diều khác để củng cố kiến thức toàn diện và đạt kết quả cao nhất trong năm học này.