Đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) Đề 4

Bài viết chia sẻ đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 4, được xây dựng dựa trên chương trình SGK Cánh Diều theo định hướng đổi mới của Bộ Giáo dục và Đào tạo. Nội dung đề thi bao quát các chuyên đề trọng tâm như hàm số bậc nhất, hệ phương trình, hệ thức lượng trong tam giác vuông, đường tròn, giúp học sinh ôn tập toàn diện kiến thức nửa đầu học kỳ I.

Ngoài ra, đề thi còn đi kèm đáp án chi tiết và hướng dẫn giải rõ ràng, giúp học sinh dễ dàng so sánh kết quả, rèn luyện kỹ năng trình bày và nâng cao hiệu quả tự học. Đây là tài liệu hữu ích cho học sinh lớp 9 trong quá trình chuẩn bị cho kỳ kiểm tra giữa kỳ theo chương trình Cánh Diều – cấu trúc mới nhất.

Họ và tên học sinh: ………………………… Lớp: …………………

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho phương trình \(2x - y = 4\). Khẳng định nào sau đây đúng?

A. Khi \(y = 0\) thì phương trình vô nghiệm.

B. Phương trình luôn vô nghiệm.

C. Phương trình có vô số nghiệm.

D. Phương trình tương đương với \(2x = 4 - y\) .

Câu 2. Nghiệm của phương trình \((2x - 3)(x + 2) = 0\) là

A. \(x = \frac{3}{2};\ x = 2\).                        B. \(x = - \frac{3}{2};\ x = 2\).

C. \(x = \frac{3}{2};\ x = - 2\).                      D. \(x = - \frac{3}{2};\ x = - 2\).

Câu 3: Điều kiện xác định của phương trình \(\frac{4x - 5}{x - 1} = 2x + \frac{1}{x^{2}}\) là: 

A. \(x \neq 1\).           B. \(x \neq - 1\).            C. \(x \neq 1\) và \(x \neq 0\).          D. \(x \neq 0\).

Câu 4: Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn?

A. \(\left\{ \begin{matrix} x^{2} - 3y = 1 \\ 4x - y = - 3 \end{matrix} \right.\)                        B. \(\left\{ \begin{matrix} x - 2y + z = 11 \\ x - 2y^{2} = - 1 \end{matrix} \right.\)

C. \(\left\{ \begin{matrix} - 4x - 2y = 5 \\ 3x - y = - 22 \end{matrix} \right.\)                      D. \(\left\{ \begin{matrix} x - 2y^{2} = 5 \\ - x - 2y = 6 \end{matrix} \right.\)

Câu 5: Bất đẳng thức \(a + 1 < 3\) có vế trái là

A. \(a + 1\).               B. \(a\).                   C. \(1\).                     D. \(3\).

Câu 6: Nghiệm của bất phương trình \(4x - 18 > 0\) là: 

A. \(x > \frac{9}{2}\).                      B. \(x > \frac{- 9}{2}\).                    C. \(x < \frac{9}{2}\).                       D. \(x < \frac{- 9}{2}\).

Câu 7: Hệ phương trình nào sau đây không tương đương với hệ \(\left\{ \begin{matrix} x + 2y = 2 \\ 3x - 2y = 1 \end{matrix} \right.\)?

A. \(\left\{ \begin{matrix} 3x + 6y = 9 \\ 3x - 2y = 1 \end{matrix} \right.\)                        B. \(\left\{ \begin{matrix} x = 3 - 2y \\ 3x - 2y = 1 \end{matrix} \right.\)

C. \(\left\{ \begin{matrix} 4x = 2 \\ x + 2y = 3 \end{matrix} \right.\)                             D. \(\left\{ \begin{matrix} 4x = 4 \\ 3x - 2y = 1 \end{matrix} \right.\)

Câu 8: Cho dãy các tỉ số lượng giác sau: \(cos14^{0};sin78^{0};cos87^{0};sin47^{0}\). Thứ tự sắp xếp các số liệu theo thứ tự tăng dần là:

A. \(sin78^{0};cos14^{0};sin47^{0};cos87^{0}\)

B. \(cos14^{0};sin78^{0};cos87^{0};sin47^{0}\)

C. \(sin47^{0};cos87^{0};sin78^{0};cos14^{0}\)

D. \(cos87^{0};sin47^{0};cos14^{0};sin78^{0}\)

Câu 9: Quan sát hình vẽ:

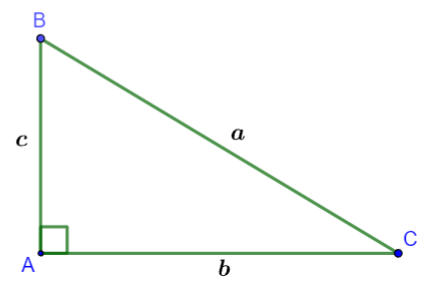
Hệ thức nào sau đây đúng?

A. \(c = a\sin\widehat{B}\)            B. \(b = a\tan\widehat{C}\)           C. \(b = c\tan\widehat{B}\)               D. \(c = a\tan\widehat{B}\)

Câu 10: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat{ABC} = 60^{0}\). Kẻ đường cao \(AH;(H \in BC)\). Kết luận nào sau đây đúng?

A. \(\frac{AH}{AB} = \frac{\sqrt{3}}{2}\)          B. \(\frac{AH}{AB} = \frac{1}{2}\)           C. \(\frac{AH}{AB} = \sqrt{3}\)                        D. \(\frac{AH}{AB} = \frac{\sqrt{3}}{3}\)

Câu 11: Quan sát hình vẽ sau:

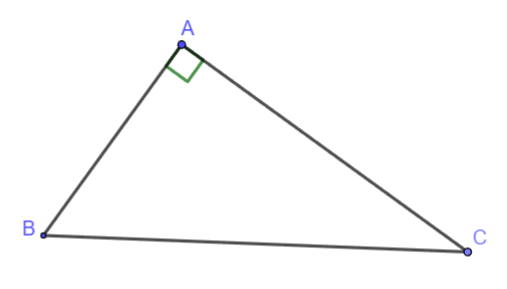
Tìm khẳng định sai trong các khẳng định sau?

A. \(\sin\widehat{B} = \cos\widehat{C}\)              B. \(\tan\widehat{C} = \frac{\sin\widehat{C}}{\cos\widehat{C}}\)               C. \(\cos\widehat{B} = \sin\widehat{C}\)           D. \(\cot\widehat{B} = \frac{1}{\tan\widehat{C}}\)

Câu 12: Cho hình vẽ:

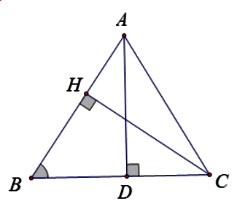
Hệ thức nào dưới đây sai?

A. \(BH = BC.tan\widehat{B}\)                 B. \(BH = BC.cos\widehat{B}\)

C. \(BC = \frac{BH}{\tan\widehat{B}}\)                        D. \(\frac{AB}{BC} = \frac{AD}{CH}\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Cho phương trình: \(\frac{2x}{2 - 5x} - \frac{x + 1}{10x - 4} - \frac{1}{4} = 0\ \ \ (1)\).

a) Điều kiện xác định của phương trình (1) là: \(x \neq \frac{5}{2}\).

b) Mẫu số chung nhỏ nhất của phương trình là \(4(2 - 5x)\).

c) Phương trình (1) biến đổi thành \(\frac{4.2x}{4(2 - 5x)} + \frac{2(x + 1)}{4(2 - 5x)} - \frac{2 - 5x}{4(2 - 5x)} = 0\).

d) Tổng các nghiệm của phương trình (1) bằng \(0\).

Câu 2: Bạn Dương có số tiền không quá \(70000\) đồng gồm \(15\) tờ tiền mệnh giá \(2000\) đồng và \(5000\) đồng. Hỏi bạn Dương có nhiều nhất bao nhiêu tờ tiền loại \(5000\) đồng? Gọi số tờ tiền loại \(5000\) đồng là \(x\) (\(x\) nguyên dương).

a) Số tờ loại \(2000\)đồng là \(x - 15\) (tờ)

b) Số tờ loại \(2000\)đồng là \(15 - x\) (tờ)

c) Số tiền loại \(5000\) đồng và \(2000\)đồng lần lượt là \(5\ 000x;\ 2\ 000(15 - x)\) (đồng)

d) Bất phương trình thỏa mãn bài toán là: O10-2024-GV154 \(5000x + 2000(15 - x) \leq 70000\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình, hệ phương trình và bất phương trình dưới đây:

a) \((x + 2)(4x - 1) = 0\)

b) \(\left\{ \begin{matrix} 4x + y = 2 \\ 8x + 3y = 5 \end{matrix} \right.\)

c) \(2(x - 3) + 5 < 3(x - 6) + 7\)

Câu 2: Giải bài toán bằng cách lập hệ phương trình

Tìm hai số nguyên dương biết tổng của nó bằng 1006, nếu lấy số lớn chia cho số bé được thương là \(2\) và số dư là \(124\).

Câu 3. a) Hãy sắp xếp các tỉ số lượng giác sau đây theo thứ tự tăng dần (có giải thích, không dùng bảng số và máy tính): cot36°; tan72°; cot21°; sin54°.

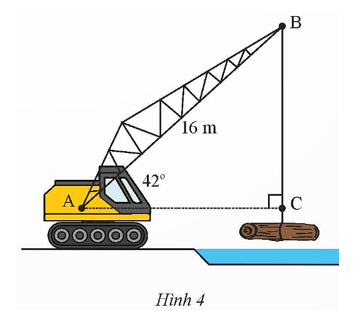
b) Một cần cẩu đang nâng một khối gỗ trên sông biết tay cẩu \(AB\) có chiều dài \(16\ m\)và nghiêng một góc \(42{^\circ}\) so với phương nằm ngang (hình vẽ). Tính chiều dài \(BC\) của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).

Câu 4. Cho \(\Delta ABC\) nhọn, các đường cao \(A D , BE, CF\).  Chứng minh rằng:

\(\frac{S_{DEF}}{S_{ABC}} = 1 - cos^{2}\ A - cos^{2}\ B - cos^{2}C\)

------------------- Hết ----------------------

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!

Thông qua đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 4 có đáp án chi tiết, học sinh có thể củng cố kiến thức nền tảng, rèn luyện tư duy và kỹ năng làm bài hiệu quả. Hãy thường xuyên luyện thêm các đề thi Toán 9 Cánh diều khác để làm quen với cấu trúc đề, nâng cao năng lực giải toán và tự tin đạt kết quả cao trong kỳ thi sắp tới.