Đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) Đề 5

Bộ đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 5 được biên soạn theo đúng định hướng chương trình SGK Cánh Diều hiện hành, giúp học sinh lớp 9 ôn tập toàn diện kiến thức trước kỳ thi giữa kỳ I. Đề thi bao gồm các dạng toán tiêu biểu trong chương trình như hàm số bậc nhất, hệ phương trình, đường tròn và các bài toán chứng minh hình học, giúp học sinh rèn luyện khả năng tư duy và củng cố kỹ năng giải bài tập.

Đặc biệt, tài liệu có đáp án chi tiết, lời giải rõ ràng, hỗ trợ học sinh tự kiểm tra, đánh giá năng lực và chuẩn bị tốt cho kỳ thi giữa học kì theo cấu trúc mới nhất của Bộ GD&ĐT. Đây là nguồn tham khảo hữu ích cho cả giáo viên và học sinh khi ôn luyện theo chương trình Toán 9 Cánh diều.

Họ và tên học sinh: ………………………… Lớp: …………………

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho biết phương trình \((x + 5)(x + 1) = 0\) có bao nhiêu nghiệm?

A. \(1\).                   B. \(2\).                 C. \(3\).                    D. \(4\).

Câu 2. Điều kiện xác định của phương trình \(\frac{12}{1 - 9x^{2}} = \frac{1 - 3x}{1 + 3x} - \frac{1 + 3x}{1 - 3x}\) là: 

A. \(x \neq \frac{1}{9}\).                                        B. \(x \neq - \frac{1}{9}\).

C. \(x \neq \frac{1}{9}\) và \(x \neq - \frac{1}{9}\).                      D. \(x \neq \frac{1}{3}\) và \(x \neq - \frac{1}{3}\).

Câu 3: Một người đi xe máy từ \(A\) đến \(B\) với vận tốc \(25\ km/h\). Lúc về, người đó đi với vận tốc \(30\ km/h\) nên thời gian về ít hơn thời gian đi là \(20\) phút. Tính quãng đường \(AB\).

A. \(40\ km\).                      B. \(70\ km\).             C. \(50\ km\).             D. \(60\ km\).

Câu 4: Cặp số nào thỏa mãn phương trình \(4x - 5y = 0\)?

A. \((0;0)\)              B. \((1;0)\)                  C. \((0;1)\)               D. \((1;1)\)

Câu 5: Trong các cách viết sau, cách viết nào không phải là bất đẳng thức

A. \(1 < 2\).              B. \(- 3 > - 1\).          C. \(a = 2\).                       D. \(3 < b\).

Câu 6: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. \(\frac{1}{2}y^{2} + 5 \geq 0\).       B. \(\frac{2}{y} - 3 > 0\).               C. \(3x - 9 > 0\).                         D. \(0.x - 6 < 0\).

Câu 7: Hệ phương trình \(\left\{ \begin{matrix} 2x - y = 1 \\ x - 2y = - 1 \end{matrix} \right.\) không tương đương với hệ phương trình nào sau đây?

A. \(\left\{ \begin{matrix} 4x - 2y = 2 \\ x - 2y = - 1 \end{matrix} \right.\)          B. \(\left\{ \begin{matrix} x - \frac{1}{2}y = \frac{1}{2} \\ x - 2y = - 1 \end{matrix} \right.\)         C. \(\left\{ \begin{matrix} 4x - 2y = 1 \\ x - 2y = - 1 \end{matrix} \right.\)           D. \(\left\{ \begin{matrix} - 2x + y = - 1 \\ x - 2y = - 1 \end{matrix} \right.\)

Câu 8: Sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần: \(cot43^{0};sin40^{0};cot40^{0};tan42^{0}\) là:

A. \(cot40^{0};cot43^{0};tan42^{0};sin40^{0}\)                B. \(cot40^{0};sin40^{0};cot43^{0};tan42^{0}\)

C. \(cot43^{0};cot40^{0};sin40^{0};tan42^{0}\)                D. \(tan42^{0};cot43^{0};cot40^{0};sin40^{0}\)

Câu 9: Quan sát hình vẽ:

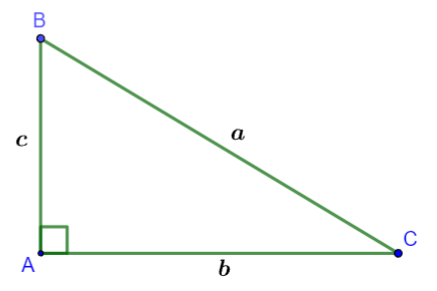
Hệ thức nào sau đây đúng?

A. \(b = a\sin\widehat{C}\)            B. \(b = a\sin\widehat{B}\)                 C. \(b = a\cos\widehat{B}\)                    D. \(b = a\tan\widehat{B}\)

Câu 10: Cho góc nhọn \(\beta\), đơn giản biểu thức \(M = 1 + tan^{2}\beta.cos^{2}\beta\) ta được kết quả là:

A. \(M = 1\)                                      B. \(M = 1 + cos^{2}\beta\)

C. \(M = 1 + sin^{2}\beta\)                        D. \(M = 2sin^{2}\beta\)

Câu 11: Cho tam giác \(ABC\) có \(\widehat{A} = 90^{0};AB = 4cm;AC = 3cm\). Khẳng định nào sau đây đúng?

A. \(\sin\widehat{C} = \frac{3}{5}\)               B. \(\cos\widehat{C} = \frac{4}{5}\)          C. \(\tan\widehat{C} = \frac{4}{3}\)               D. \(\cot\widehat{B} = \frac{3}{2}\)

Câu 12: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat{C} = 30^{0};b = 10\). Xác định giá trị của \(c\)?

A. \(c = \frac{10\sqrt{3}}{3}\)               B. \(c = 10\sqrt{3}\)                     C. \(c = 20\)                    D. \(c = 5\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Cho phương trình \(\frac{6x - 1}{3x + 2} = \frac{2x + 5}{x - 3}\), khi đó:

a) Điều kiện xác định \(x \neq \frac{- 2}{3}\) và \(x \neq 3\).

b) Nghiệm của phương trình là một nghiệm nguyên.

c) Nghiệm của phương trình là \(x = 3\).

d) Nghiệm của phương trình là \(x = - \frac{7}{38}\).

Câu 2: Quãng đường đi từ A đến B dài \(50\) km. Một ô tô đi từ A đến B, khởi hành lúc \(7\) giờ. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước \(9\) giờ cùng ngày ? Gọi \(x\) là vận tốc của ô tô (\(x > 0\), km/h).

a) Thời gian đi từ A đến B là \(2\) giờ.

b) Thời gian đi từ A đến B là \(\frac{50}{x}\) (giờ)

c) Để đến B trước \(9\) giờ thì thời gian đi cần nhỏ hơn hoặc bằng \(2\).

d) Bất phương trình thỏa mãn bài toán là \(\frac{50}{x} < 2\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình, hệ phương trình và bất phương trình dưới đây:

a) \(\left\{ \begin{matrix} 0,2x + 0,1y = 0,3 \\ 3x + y = 5 \end{matrix} \right.\)                               b) \(\frac{x - 3}{x - 5} + \frac{1}{x} = \frac{x + 5}{x(x - 5)}\)

c) \(5(x - 3) + 7 > 2(x + 3) - 11\)

Câu 2: Giải bài toán bằng cách lập hệ phương trình

Một cano đi xuôi dòng từ địa điểm \(A\) đến địa điểm \(B\) và lại ngược dòng từ địa điểm \(B\) về địa điểm \(A\) mất \(9\) giờ, tốc độ của cano khi nước yên lặng không đổi trên suốt quãng đường đó và tốc độ của dòng nước cũng không đỏi khi cano chuyển động. Biết thời gian cano đi xuôi dòng \(5km\) bằng thời gian cano đi ngược dòng \(4km\) và quãng đường \(AB\) dài \(160km\). Tính tốc độ của cano khi nước yên lặng và tốc độ của dòng nước.

Câu 3. Ca nô dù bay là một trò chơi thể thao mạo hiểm được ưa chuộng trong đó người chơi được đeo dù và được canô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao (xem hình vẽ). Biết độ dài của dây kéo \(AC = 160\ m\) và góc tạo bởi dây kéo và phương nằm ngang \(\widehat{ACB} = 25{^\circ}\).

a) Tính độ cao \(AB\) của người chơi so với mặt biển.

b) Muốn bay cao \(75\ m\) thì dây kéo phải dài bao nhiêu mét (làm tròn kết quả đến hàng phần mười mét)?

Câu 4. Người ta dùng 100 m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.

------------------- Hết ----------------------

Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!

Với đề thi giữa học kì 1 Toán 9 Cánh diều (Cấu trúc mới) – Đề 5 có đáp án chi tiết, học sinh không chỉ được rèn kỹ năng giải toán mà còn làm quen với cấu trúc đề thi thực tế. Hãy tiếp tục luyện tập thêm các đề thi Toán 9 Cánh diều khác để củng cố kiến thức, cải thiện tốc độ làm bài và tự tin đạt kết quả cao trong kỳ thi giữa kỳ I sắp tới.