Đề thi giữa học kì 1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 1

Bạn đang tìm kiếm đề thi giữa học kì 1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 1 kèm đáp án chi tiết để ôn tập và kiểm tra năng lực? Bài viết này sẽ cung cấp cho bạn bộ đề thi chuẩn theo chương trình Chân trời sáng tạo, bám sát cấu trúc mới của Bộ Giáo dục, giúp học sinh lớp 9 rèn luyện kỹ năng giải bài tập, củng cố kiến thức trọng tâm và làm quen với dạng đề thường gặp. Ngoài ra, phần đáp án chi tiết đi kèm sẽ hỗ trợ các em đối chiếu kết quả, nắm vững phương pháp giải, từ đó nâng cao hiệu quả học tập và chuẩn bị tốt cho kỳ thi.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Trong các phương trình sau, phương trình là phương trình bậc nhất hai ẩn là

A. \(- 5x + 0y = 6\).              B. \(0x + 0y = 1\).        C. \(5x - 3 = 0\).                 D. \(5x - 3y = 10\)

Câu 2. Trong các hệ phương trình sau, hệ phương trình bậc nhất hai ẩn là

A. \(\left\{ \begin{matrix} x + y = 5 \\ 2x - 3y = 5 \end{matrix} \right.\)            B. \(\left\{ \begin{matrix} x + y = 5 \\ x - z = 2 \end{matrix} \right.\)        C. \(\left\{ \begin{matrix} 2x - y = 2 \\ 2t - 3y = 5 \end{matrix} \right.\)             D. \(\left\{ \begin{matrix} x + y = 5 \\ 2x^{2} - 3y = 5 \end{matrix} \right.\)

Câu 3: Cặp số \(\left( x_{0};y_{0} \right)\)là một nghiệm của hệ phương trình \(\left\{ \begin{matrix} ax + by = c\ \ \ \ \ \ \ \ \ \ \ (1) \\ a'x + b'y = c'\ \ \ \ \ (2) \end{matrix} \right.\) nếu

A. \(\left( x_{0};y_{0} \right)\) là nghiệm của phương trình \((1)\).

B. \(\left( x_{0};y_{0} \right)\) là nghiệm của phương trình \((2)\).

C. \(\left( x_{0};y_{0} \right)\) là nghiệm của một trong hai phương trình.

D. \(\left( x_{0};y_{0} \right)\) là nghiệm chung của hai phương trình \((1)\)và \((2)\).

Câu 4: Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{matrix} x + 2y = 3 \\ y = 1 \end{matrix} \right.\)?

A. \((2;1)\).                   B. \((2; - 1)\).                 C. \((1; - 1)\).                     D. \((1;1)\).

Câu 5: Hệ thức \(4 \geq 8\)

A. là một đẳng thức.

B. là một bất đẳng thức với \(4\)là vế phải của bất đẳng thức.

C. là một bất đẳng thức với \(4\)là vế trái và \(8\) là vế phải của bất đẳng thức.

D. là một bất đẳng thức với \(4\)là vế phải và \(8\) là vế trái của bất đẳng thức.

Câu 6: Bất phương trình dạng \(ax + b > 0\)(hoặc \(ax + b < 0,\ ax + b \geq 0,ax + b \leq 0\)) là bất phương trình bậc nhất một ẩn (ẩn là \(x\)) với điều kiện:

A. \(a,\ b\) là hai số đã cho.                      B. \(a,\ b\) là hai số đã cho và \(a\) khác \(0\).

C. \(a\) khác \(0\).                                         D. \(a\) và \(b\) khác \(0\).

Câu 7: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn ?

A. \(x + y - 1 > 0\).             B. \(x - 1 > 0\)               C. \(x + y > 0\).              D. \(x - y > 0\).

Câu 8: Với 3 số a, b, c và a \(\geq\) b thì:

A. Nếu c \(>\) \(0\) thì a.c \(\leq\) b.c.                      B. Nếu c \(< 0\) thì a.c \(>\) b.c.

C. Nếu c \(<\) \(0\) thì a.c \(\geq\) b.c.                     D. Nếu c \(> 0\)thì a.c \(\geq\) b.c.

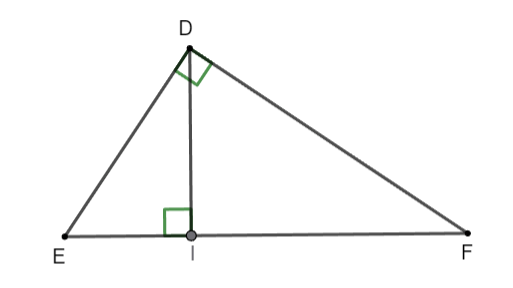
Cho tam giác \(DEF\) có \(\widehat{D} = 90^{0}\), đường cao \(DI\). Hãy trả lời các câu hỏi từ câu 9 đến câu 11.

Câu 9: \(\sin\widehat{E}\) bằng:

A. \(\frac{DE}{EF}\)               B. \(\frac{DI}{DE}\)                 C. \(\frac{DI}{EI}\)                 D. \(\frac{DF}{ D E}\)

Câu 10: \(\tan\widehat{E}\) bằng

A. \(\frac{DE}{EF}\)               B. \(\frac{EI}{DI}\)                  C. \(\frac{DI}{EI}\)                 D. \(\frac{DF}{EF}\)

Câu 11: \(\cos\widehat{F}\) bằng:

A. \(\frac{DE}{EF}\)               B. \(\frac{DI}{EF}\)              C. \(\frac{DI}{IF}\)                           D. \(\frac{DF}{EF}\)

Câu 12: Một tam giác vuông có cạnh huyền bằng \(8cm\), một góc nhọn bằng \(70^{0}\). Độ dài cạnh góc vuông kề với góc nhọn này bằng (làm tròn đến chữ số thập phân thứ hai)

A. \(7,52cm\)             B. \(2,73cm\)             C. \(2,74cm\)                 D. \(7,51cm\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Cho phương trình \(\frac{6x - 1}{3x + 2} = \frac{2x + 5}{x - 3}\), khi đó:

a) Điều kiện xác định \(x \neq \frac{- 2}{3}\) và \(x \neq 3\).

b) Nghiệm của phương trình là một nghiệm nguyên.

c) Nghiệm của phương trình là \(x = 3\).

d) Nghiệm của phương trình là \(x = - \frac{7}{38}\).

Câu 2: Quãng đường đi từ A đến B dài \(50\) km. Một ô tô đi từ A đến B, khởi hành lúc \(7\) giờ. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước \(9\) giờ cùng ngày ? Gọi \(x\) là vận tốc của ô tô (\(x > 0\), km/h).

a) Thời gian đi từ A đến B là \(2\) giờ.

b) Thời gian đi từ A đến B là \(\frac{50}{x}\) (giờ)

c) Để đến B trước \(9\) giờ thì thời gian đi cần nhỏ hơn hoặc bằng \(2\).

d) Bất phương trình thỏa mãn bài toán là \(\frac{50}{x} < 2\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình và bất phương trình dưới đây:

a) \((x + 5)(x + 1) = 0\)                       b) \(2x + \frac{2x + 1}{2} > 3x - \frac{1}{5}\)

Câu 2:

a) Tìm cặp số \((x;y)\) thỏa mãn hệ phương trình: \(\left\{ \begin{matrix} 3x + 2y = 7 \\ x - 7y = - 13 \end{matrix} \right.\).

b) Giải bài toán bằng cách lập hệ phương trình

Tìm số tự nhiên \(N\)có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai chữ số của số \(N\) theo thứ tự ngước lại thì được một số nhở hơn số \(N\) là \(18\) đơn vị?

Câu 3. Chiều cao của cột đèn (như hình vẽ)

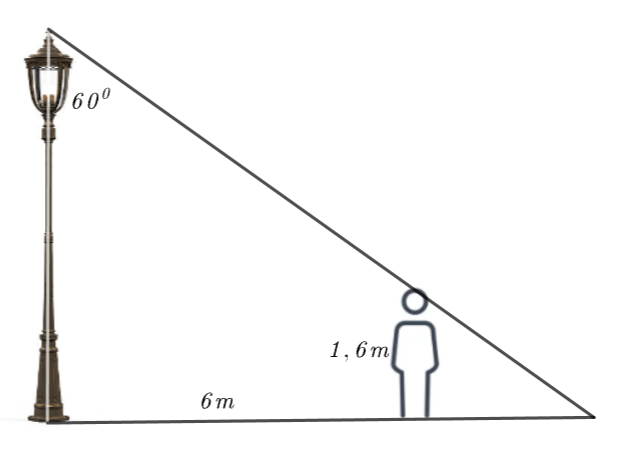
Một học sinh đứng cách cột đèn 6m, cột đèn tạo với đoạn nối điểm cao nhất của cột đèn và điểm cao nhất của học sinh một góc \(\widehat{BDC} = 60^{0}\). Tính chiều cao của cột đèn, biết rằng chiều cao của học sinh là \(1,6m\)? (Kết quả làm tròn đến chữ số thập phân thứ nhất).

Câu 4. Cho \(x;y\) là các số dương thỏa mãn \((4x + 6y + 2019).(x - y + 3) = 0\). Tìm giá trị nhỏ nhất của \(P = xy - 5x + 2020\).

------------------- Hết ----------------------

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ.

Với đề thi giữa hk1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 1 kèm đáp án chi tiết, học sinh không chỉ được làm quen với cấu trúc đề thi thực tế mà còn củng cố chắc kiến thức, rèn luyện kỹ năng giải toán logic và khoa học. Hãy lưu lại tài liệu, luyện tập thường xuyên để đạt kết quả cao trong kỳ thi giữa học kì 1 sắp tới.