Đề thi giữa học kì 1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 5

Kỳ thi giữa học kì 1 là dịp để học sinh lớp 9 đánh giá năng lực học tập và rèn luyện kỹ năng giải toán. Nhằm hỗ trợ học sinh ôn tập hiệu quả, bài viết này giới thiệu đề thi giữa học kì 1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 5 kèm đáp án chi tiết. Đề thi được biên soạn bám sát chương trình Toán 9 theo bộ sách Chân trời sáng tạo, phù hợp với cấu trúc ra đề hiện hành, giúp học sinh làm quen với các dạng toán từ cơ bản đến nâng cao. Đồng thời, phần đáp án và hướng dẫn giải chi tiết sẽ giúp học sinh dễ dàng đối chiếu, tự rèn luyện và củng cố kiến thức một cách khoa học, chuẩn bị vững vàng cho kỳ thi.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1. Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?

A. \(2x - 3y = 5.\)         B. \(0x + 2y = 4.\)          C. \(2x - 0y = 3.\)          D. \(0x - 0y = 6.\)

Câu 2. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn?

A. \(\left\{ \begin{matrix} 2x + 3y^{2} = 1 \\ - 3x = 18. \end{matrix} \right.\)                                   B. \(\left\{ \begin{matrix} 0,5x - 0,2y = - 0,1 \\ 0x + 0y = - 0,4. \end{matrix} \right.\)

C. \(\left\{ \begin{matrix} - 4x + 7y = - 10 \\ 3x + 8y = - 19. \end{matrix} \right.\)                              D.\(\left\{ \begin{matrix} x + 3y = 2 \\ 31x^{2} + 5y^{2} = - 1. \end{matrix} \right.\)

Câu 3. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. \(- 2x^{2} + 5 > 0\).                     B. \(3x - y \leq 0\).

C. \(- 4x - 2 < 0\).                      D. \(5 + 0x \geq - 7\).

Câu 4. Điều kiện xác định của phương trình \(\frac{4x - 5}{x - 1} = 2x + \frac{1}{x^{2}}\) là: 

A. \(x \neq 1\).         B. \(x \neq - 1\).             C. \(x \neq 1\) và \(x \neq 0\).               D. \(x \neq 0\).

Câu 5: Tập nghiệm của bất phương trình: \(x - 2 > 0\) là:

A. \(x > 2\)              B. \(x < 2\)                  C. \(x \geq 2\)                 D. \(x \leq 2\)

Câu 6: Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,\ ax + b \geq 0,ax + b \leq 0\)) là bất phương trình bậc nhất một ẩn (ẩn là \(x\)) với điều kiện:

A. \(a,\ b\) là hai số đã cho                   B. \(a,\ b\) là hai số đã cho và \(a\) khác \(0\).

C. \(a\) khác \(0\).                                     D. \(a\) và \(b\) khác \(0\).

Câu 7: Hệ thức \(2a \leq a + 1\) là một bất đẳng thức và

A. \(a + 1\) là vế trái, \(2a\) là vế phải B. \(a + 1\) là vế trước, \(2a\) là vế sau

C. \(a + 1\) là vế sau, \(2a\) là vế trước D. \(a + 1\) là vế phải, \(2a\) là vế trai

Câu 8: Cho bất phương trình \(5 - 5x > 0\) có:

Câu 8: Cho bất phương trình \(5 - 5x > 0\) có:

A. \(a = 5;b = - 5\)                   B. \(a = - 5;b = 5\)

C. \(a = 5;b = 5\)                     D. \(a = - 5;b = - 5\)

Câu 9: Cho \(\alpha\) và \(\beta\) là hai góc phụ nhau, khi đó:

A. \(\sin\alpha = \cos\beta\).      B.  \(\sin\alpha = \cot\beta\).      C. \(\sin\alpha = \tan\beta\).          D. \(\cos\alpha = \cot\beta\).

Sử dụng hình sau để trả lời các câu hỏi

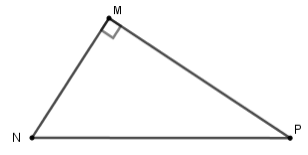
Câu 10: \(\sin\widehat{P}\) bằng:

A. \(\frac{MN}{MP}\)                B. \(\frac{MP}{NP}\)              C. \(\frac{MP}{MN}\)         D.\(\frac{MN}{NP}\)

Câu 11: \(\tan\widehat{N}\) bằng:

A. \(\frac{MN}{NP}\)       B. \(\frac{MP}{NP}\)      C. \(\frac{MN}{MP}\)      D.\(\frac{MP}{MN}\)

Câu 12: Hệ thức nào sau đây là sai?

A. \(MN = NP.sin\widehat{P}\)                   B. \(MN = NP.sin\widehat{N}\)

C. \(MN = NP.cos\widehat{N}\)                   D. \(MN = MP.tan\widehat{P}\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Cho phương trình: \(\frac{2x}{2 - 5x} - \frac{x + 1}{10x - 4} - \frac{1}{4} = 0\ \ \ (1)\).

a) Điều kiện xác định của phương trình (1) là: \(x \neq \frac{5}{2}\).

b) Mẫu số chung nhỏ nhất của phương trình là \(4(2 - 5x)\).

c) Phương trình (1) biến đổi thành \(\frac{4.2x}{4(2 - 5x)} + \frac{2(x + 1)}{4(2 - 5x)} - \frac{2 - 5x}{4(2 - 5x)} = 0\).

d) Tổng các nghiệm của phương trình (1) bằng \(0\).

Câu 2: Bạn Dương có số tiền không quá \(70000\) đồng gồm \(15\) tờ tiền mệnh giá \(2000\) đồng và \(5000\) đồng. Hỏi bạn Dương có nhiều nhất bao nhiêu tờ tiền loại \(5000\) đồng? Gọi số tờ tiền loại \(5000\) đồng là \(x\) (\(x\) nguyên dương).

a) Số tờ loại \(2000\) đồng là \(x - 15\) (tờ)

b) Số tờ loại \(2000\) đồng là \(15 - x\) (tờ)

c) Số tiền loại \(5000\) đồng và \(2000\) đồng lần lượt là \(5\ 000x;\ 2\ 000(15 - x)\) (đồng)

d) Bất phương trình thỏa mãn bài toán là: \(5000x + 2000(15 - x) \leq 70000\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình và hệ phương trình dưới đây:

a) \(2x(3x - 5) = 10 - 6x\)                b) \(\left\{ \begin{matrix} 0,5x + 2y = - 2,5 \\ 0,7x - 3y = 8,1 \end{matrix} \right.\)

Câu 2: Giải bài toán bằng cách lập hệ phương trình

Một hợp tác vận tải có \(15\) xe ô tô nhỏ và \(10\) xe ô tô lớn thì vận chuyển được \(690\) khách. Nếu hợp tác vận tải rút bớt \(10\) xe ô tô nhỏ và tăng thêm \(4\) xe ô tô lớn thì số khách chuyển được tăng thêm \(20\) người . Hỏi mỗi loại xe chở được bao nhiêu người.

Câu 3. Cho tam giác \(ABC\) vuông ở A, có \(AC = 15cm,B = 50^{0}\). Hãy tính độ dài:

a) \(AB,BC\).

b) Phân giác \(CD.\)

Câu 4. Tìm giá trị nhỏ nhất của biểu thức \(A = x^{2} + 5y^{2} + 2x - 10y + 14\)?

------------------- Hết ----------------------

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

Với đề thi giữa hk1 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 5 và đáp án chi tiết, học sinh sẽ có thêm tài liệu tham khảo hữu ích để ôn tập toàn diện, rèn kỹ năng giải toán và tự tin bước vào kỳ thi. Hãy luyện tập thường xuyên với nhiều dạng đề để đạt kết quả cao nhất trong kỳ thi giữa học kì 1.