Đề thi giữa học kì 1 Toán 9 Kết nối tri thức (Cấu trúc mới) Đề 1

Chào các bạn học sinh và phụ huynh! Trong bài viết này, chúng tôi giới thiệu đến các bạn đề thi giữa học kì 1 môn Toán lớp 9 theo bộ sách Kết nối tri thức (cấu trúc mới). Đề thi được biên soạn bám sát chương trình học, giúp học sinh ôn luyện hiệu quả và chuẩn bị tốt nhất cho kỳ thi học kỳ. Bên cạnh đó, bài viết còn cung cấp đáp án chi tiết, giúp các bạn dễ dàng theo dõi và hiểu rõ hơn về các phương pháp giải toán. Hãy cùng khám phá và ôn luyện ngay hôm nay để đạt kết quả cao trong kỳ thi giữa học kỳ 1!

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1. Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?

A. \(2x - 3y = 5.\)                      B. \(0x + 2y = 4.\)

C. \(2x - 0y = 3.\)                     D. \(0x - 0y = 6.\)

Câu 2. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn?

A. \(\left\{ \begin{matrix} 2x + 3y^{2} = 1 \\ - 3x = 18. \end{matrix} \right.\)                          B. \(\left\{ \begin{matrix} 0,5x - 0,2y = - 0,1 \\ 0x + 0y = - 0,4. \end{matrix} \right.\)

C. \(\left\{ \begin{matrix} - 4x + 7y = - 10 \\ 3x + 8y = - 19. \end{matrix} \right.\)                     D.\(\left\{ \begin{matrix} x + 3y = 2 \\ 31x^{2} + 5y^{2} = - 1. \end{matrix} \right.\)

Câu 3. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. \(- 2x^{2} + 5 > 0\).                 B. \(3x - y \leq 0\).

C. \(- 4x - 2 < 0\).                  D. \(5 + 0x \geq - 7\).

Câu 4. Điều kiện xác định của phương trình \(\frac{4x - 5}{x - 1} = 2x + \frac{1}{x^{2}}\) là: 

A. \(x \neq 1\).            B. \(x \neq - 1\).              C. \(x \neq 1\) và \(x \neq 0\).                 D. \(x \neq 0\).

Câu 5: Tập nghiệm của bất phương trình: \(x - 2 > 0\) là

A. \(x > 2\)                    B. \(x < 2\)                    C. \(x \geq 2\)                 D. \(x \leq 2\)

Câu 6: Bất phương trình dạng \(ax + b > 0\)(hoặc \(ax + b < 0,\ ax + b \geq 0,ax + b \leq 0\)) là bất phương trình bậc nhất một ẩn (ẩn là \(x\)) với điều kiện:

A. \(a,\ b\) là hai số đã cho                       B. \(a,\ b\) là hai số đã cho và \(a\) khác \(0\).

C. \(a\) khác \(0\).                                         D. \(a\)và \(b\) khác \(0\).

Câu 7: Hệ thức \(2a \leq a + 1\) là một bất đẳng thức và

A. \(a + 1\) là vế trái, \(2a\) là vế phải                            B. \(a + 1\) là vế trước, \(2a\) là vế sau

C. \(a + 1\) là vế sau, \(2a\) là vế trước                         D. \(a + 1\) là vế phải, \(2a\) là vế trái

Câu 8: Cho bất phương trình \(5 - 5x > 0\) có:

A. \(a = 5;b = - 5\)                 B. \(a = - 5;b = 5\)  

C. \(a = 5;b = 5\)                  D. \(a = - 5;b = - 5\)

Câu 9: Cho \(\alpha\) và \(\beta\) là hai góc phụ nhau, khi đó:

A. \(\sin\alpha = \cos\beta\).                         B.  \(\sin\alpha = \cot\beta\).

C. \(\sin\alpha = \tan\beta\).                          D. \(\cos\alpha = \cot\beta\).

Sử dụng hình sau để trả lời các câu hỏi

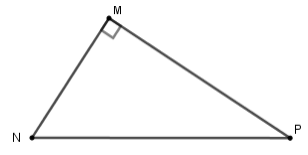
Câu 10: \(\sin\widehat{P}\) bằng:

A. \(\frac{MN}{MP}\)                  B. \(\frac{MP}{NP}\)                 C. \(\frac{MP}{MN}\)                D.\(\frac{MN}{NP}\)

Câu 11: \(\tan\widehat{N}\) bằng:

A. \(\frac{MN}{NP}\)                 B. \(\frac{MP}{NP}\)               C. \(\frac{MN}{MP}\)                D.\(\frac{MP}{MN}\)

Câu 12: Hệ thức nào sau đây là sai?

A. \(MN = NP.sin\widehat{P}\)                   B. \(MN = NP.sin\widehat{N}\)

C. \(MN = NP.cos\widehat{N}\)                   D. \(MN = MP.tan\widehat{P}\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Cho bất phương trình \(2(x - 2) \geq 3(1 - x) + 2\ \ \ \ (*)\).

a) Nhân phân phối hai vế của bất phương trình (*) ta được: \(2x - 4 \geq 3 - 3x + 2\).

b) Rút gọn bất phương trình (*) ta được \(- x \geq 9\).

c) Nghiệm của bất phương trình (*) là \(x \leq - 9\).

c) Nghiệm nguyên nhỏ nhất của bất phương trình (*) là: \(x = 1\).

Câu 2: Cho hệ phương trình \(\left\{ \begin{matrix} x - 2y = 5\ \ \ (1) \\ 2x - y = 7\ \ \ (2) \end{matrix} \right.\).

a) Cặp số \(( - 3;1)\) là một nghiệm của hệ phương trình đã cho.

b) Nhân hai vế của phương trình (*) với 2 ta được hệ phương trình mới là: \(\left\{ \begin{matrix} 2x - 4y = 10 \\ 2x - y = 7 \end{matrix} \right.\).

c) Hệ phương trình đã cho có nghiệm \((x;y) = (3; - 1)\).

d) Biết nghiệm của hệ phương trình đã cho cũng là nghiệm của phương trình \((m - 1)x + 2my = 2m + 1\). Khi đó \(m = 4\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình và bất phương trình dưới đây:

a) \(\frac{2x + 1}{x + 1} + \frac{2}{x} = \frac{2}{x(x + 1)}.\)                      b) \(\frac{2x - 1}{3} - \frac{x + 2}{2} < \frac{5x + 4}{6}.\)

Câu 2: a) Tìm các hệ số \(x\) và \(y\) (\(x;y\mathbb{\in Z}\)) trong phản ứng hóa học đã được cân bằng sau:

\(xKClO_{3} \rightarrow 2KCl + yO_{2}.\)

Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng rồi xác định giá trị của biểu thức \(T = x + 2y\)?

b) Giải bài toán bằng cách lập hệ phương trình

Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ, người thứ hai làm 6 giờ thì chỉ hoàn thành được 25% công việc. Hỏi nếu làm riêng thì người thứ nhất và người thứ hai hoàn thành lần lượt trong bao lâu?

Câu 3. Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết\(\frac{HD}{HA} = \frac{3}{2}\). Khi đó \(\tan\widehat{ABC}.tan\widehat{ACB} = \frac{a}{b}\), với \(\frac{a}{b}\) là phân số tối giản; \(a;b\mathbb{\in Z}\). Tính \(a + b\)?

Câu 4. Cho một tấm nhôm hình vuông cạnh \(2016\)(cm). Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\)(cm) rồi gập tấm nhôm lại để được một cái hộp không nắp. Tìm \(x\)để hộp nhận được có thể tích lớn nhất?

------------------- Hết ----------------------

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

Hy vọng rằng đề thi giữa học kì 1 môn Toán lớp 9 của bộ sách Kết nối tri thức (cấu trúc mới) sẽ là tài liệu hữu ích giúp các bạn học sinh ôn luyện hiệu quả. Đừng quên tham khảo thêm các đề thi khác để làm quen với các dạng bài tập và nâng cao kỹ năng giải toán. Chúc các bạn có một kỳ thi học kỳ 1 đạt kết quả xuất sắc