Đề thi học sinh giỏi lớp 12 THPT tỉnh Tuyên Quang năm 2010 - 2011

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi học sinh giỏi lớp 12 THPT tỉnh Tuyên Quang năm 2010 - 2011.

Đề thi học sinh giỏi môn Toán và Văn:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TUYÊN QUANG ĐỀ THI CHÍNH THỨC

KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 NĂM HỌC: 2010 - 2011

ĐỀ THI MÔN: TOÁN

Câu 1. (4 điểm):

a) Giải hệ phương trình: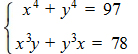

b) Giải phương trình:

Câu 2. (4 điểm):

a) Tìm các số nguyên tố x, y là nghiệm của phương trình: x² - 2y² - 1 = 0

b) Cho n là 1 số tự nhiên. Chứng minh:

Câu 3. (4 điểm):

Cho dãy số (U_n) xác định bởi: 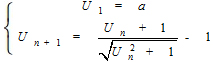trong đó -1 < a < 0

a) Chứng minh rằng: - 1 < U_n < 0 với n thuộc ¥ và (U_n) là một dãy số giảm.

b) Chứng minh rằng: với n thuộc ¥

Câu 4. (4 điểm):

Đối với hệ tọa độ Oxy cho 2 điểm A(- 1; 0); B(1; 0) và đường thẳng d có phương trình: ax + by + 1 = 0 tiếp xúc với đường tròn (C) có phương trình: x² + y² = 1. Tìm giá trị nhỏ nhất của tổng khoảng cách từ A và B đến đường thẳng d.

Câu 5. (4 điểm):

Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, tâm O. Đường cao của hình chóp là SA = a. M là một điểm di động trên SB, đặt BM = x√2. là mặt phẳng qua OM và vuông góc với (ABCD).

a) Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α). Tính diện tích thiết diện theo a và x.

b) Xác định x để thiết diện là hình thang vuông. Trong trường hợp đó tính thể tích của hai phần của S.ABCD chia bởi thiết diện.

ĐỀ THI MÔN: NGỮ VĂN

Câu 1: (8,0 điểm)

Trong Truyện Kiều, kết thúc đoạn thơ Kiều gặp Kim Trọng, Nguyễn Du viết:

“Bóng tà như giục cơn buồn,
Khách đà lên ngựa, người còn ghé theo
Dưới cầu nước chảy trong veo,
Bên cầu tơ liễu bóng chiều thướt tha”

Đoạn thơ trên nói đến “cảnh” nhưng lại nói nhiều đến “tình”. Em hãy viết một bài văn (không quá 1 trang giấy thi để làm rõ điều đó).

Câu 2: (12 điểm)

Phân tích sắc thái riêng biệt của bài thơ Thu vịnh (Nguyễn Khuyến) và bài thơ Đây mùa thu tới (Xuân Diệu).