Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Đề thi học kì 2 Toán 8 Kết nối tri thức - Đề 6

Đề thi cuối kì 2 Toán 8 KNTT có đáp án và ma trận

Tải về

Đề thi cuối kì 2 Toán 8 năm 2024 có đáp án

Đề thi học kì 2 Toán 8 Kết nối tri thức - Đề 6 có đầy đủ đáp án và ma trận, thầy cô có thể tham khảo ra đề kiểm tra và làm tài liệu ôn luyện cho các em học sinh. Đây cũng là tài liệu hay giúp các em học sinh ôn tập, làm quen với nhiều dạng đề khác nhau, chuẩn bị cho kì thi cuối học kì 2 Toán 8 sắp tới đạt kết quả cao. Mời các bạn tải về tham khảo toàn bộ đề thi, đáp án, ma trận và bảng đặc tả đề thi.

Để chuẩn bị cho kì thi học kì 2 sắp tới, các em học sinh cần thực hành luyện tập để làm quen với nhiều dạng đề khác nhau cũng như nắm được các dạng bài thường có trong đề thi. Chuyên mục Đề thi học kì 2 lớp 8 trên VnDoc tổng hợp đề thi tất cả các môn, là tài liệu hay cho các em học sinh ôn tập và luyện đề.

1. Ma trận đề thi cuối học kì 2 Toán 8 KNTT

PHẦN I: TRẮC NGHIỆM (3,0 điểm) Hãy viết lại chữ cái đứng trước câu trả lời đúng.

Câu 1. [TH] Phương trình (x-5).(x+10) = 0 có tập nghiệm là:

A. {5 }

B.{ - 10 }

C.{5 ; -10}

D. {- 5;10}

Câu 2.[TH] Số nào sau đây là nghiệm của phương trình: 3x + 4 = x - 2

A. -3.

B. 1.

C. $\frac{-3}{2}$ $\frac{-3}{2}$

D. -6.

Câu 3. [NB] Bất phương trình bậc nhất một ẩn là :

A. 0x + 6 > 0

B.2x – 5 > 7

C.x² + 3 < 0

D.(x -2 )( 2x – 3 ) >o

Câu 4.[NB ] Bất phương trình 3x +1 > -5 có nghiệm là:

A.x > -2

B. x < -2

C. x -2

D. x -2

Câu 5. [NB] Đường thẳng nào sau đây đi qua gốc tọa độ?

A.y = 2x

B. y = x + 2

C. x + y =1

D. x = y + 1

Câu 6 . [NB] Hệ số góc của đường thẳng y = 3x + 4 là:

A.4

B. 3

C. 7

D. 12

Câu 7. [TH] Vị trí tương đối của hai đương thẳng (d): y = x +1 và (d’): 2x + y= 3 là:

A.song song

B. trùng nhau

C. cắt nhau

D. vuông góc

Câu 8.[TH] Cho 2 đường thẳng (d): y= ax + b; (d’): y = a’x + b’. Hai đường thẳng (d) và (d’) song song với nhau khi:

A.a = a’

B. a ≠ a’

C. a = a’; b ≠ b’

D. a = a’; b = b’

Câu 9.[NB_ TN6] Hình chóp tam giác đều có số cạnh đáy là

A.3

B.4

C.5

D.6

Câu 10.[NB] Hình chóp đều có chiều cao , diện tích đáy . Khi đó, thể tích của hình chóp đều bằng :

Câu 11. [TH] Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là: 5cm ; 3cm ; 2cm. Thể tích của hình hộp chữ nhật là:

A. 54 cm³

B. 54 cm²

C. 30 cm²

D. 30 cm³

Câu 12.[TH]. Diện tích toàn phần của một lăng trụ đứng ,đáy tam giac vuông có hai cạnh góc vuông là 3cm ;4cm.

A. 12 cm²

B. 108 cm²

C. 7 cm²

D. 120 cm²

PHẦN II: TỰ LUẬN (7,0 điểm)

Câu 13. [TH]. (1,5 điểm) Giải các phương trình sau

a. 5 x - 2 = 3 x + 10

b. (x + 2)(3x - 15) = 0

Câu 14. [TH] (1.0 điểm) Giải bất phương trình và biểu diễn nghiệm trên trục số:

4x - 3 > 3x + 2

Câu 15. (1,0 điểm) [VD] Tính xác suất thực nghiệm của biến cố “ Mặt xuất hiện của đồng xu là mặt N” trong mỗi trường hợp sau :

a) Tung một đồng xu 30 lần liên tiếp, có 6 lần xuất hiện mặt N.

b) Tung một đồng xu 22 lần liên tiếp, có 8 lần xuất hiện mặt S.

c) Tung một đồng xu 10 lần liên tiếp, có 4 lần xuất hiện mặt N.

d) Tung một đồng xu 18 lần liên tiếp, có 9 lần xuất hiện mặt S.

Câu 16. [VD - VDC] (3,0 điểm) Cho tam giác ABC vuông tại A, có AB = 12 cm ; AC = 16 cm. Kẻ đường cao AH HBC).

a) Chứng minh: HBA ഗ ABC

b. Tính độ dài các đoạn thẳng BC, AH.

c) Trong ABC kẻ phân giác AD (DBC). Trong ΔADB kẻ phân giác DE (E∈AB); trong ΔADC kẻ phân giác DF (F∈AC).

Chứng minh rằng:

Câu 17. (0,5 điểm) [VDC]. Giải phương trình: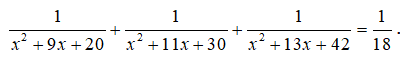

2. Đáp án đề thi cuối kì 2 Toán 8 KNTT

I . TRẮC NGHIỆM (3 ĐIỂM) (Mỗi câu đúng 0.25 điểm).

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5	Câu 6	Câu 7	Câu 8	Câu 9	Câu 10	Câu 11	Câu 12
C	A	B	A	A	B	C	C	A	D	D	C

3. Ma trận đề kiểm tra Toán cuối kì 2 lớp 8

TT	Chủ đề	Nội dung/Đơn vị kiến thức	Mức độ đánh giá								Tổng % điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TNKQ	TL	TNKQ	TL	TNKQ	TL	TNKQ	TL
1	Phương trình	Phương trình bậc nhất một ẩn , phương trình tích , phương trình chứa ẩn ở mẫu, giải bài toán bằng cách lập phương trình			2 Câu 1,2 0,5đ	1 Câu 13 1.5đ				1 Câu 17 0.5đ	2,5
2	Bất phương trình bậcnhất mộtẩn	Bất đẳng thức. Bất phương trình bậc nhất một ẩn	2 Câu 3,4 0.5đ					1 Câu 14 1.0đ			1,5
3	Hàm số và đồ thị	Hàm số và đồ thị	2 Câu 5,7 0.5đ		2 Câu 6,8 0.5đ						1,0
4	Phân tích và xử lí dữ liệu	Mô tả xác suất của biến cố ngẫu nhiên trong một số ví dụ đơn giản. Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó				1 Câu 15 1,0đ					1,0
5	Các hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương			1 Câu 10 0,25đ						1,0
5	Các hình khối trong thực tiễn	Lăng trụ đứng tam giác, lăng trụ đứng tứ giác, hình chóp	2 Câu 9,11 0,5đ				1 Câu 12 0,25đ				1,0
6	Định lí Thalès trong tam giác	Định lí Thalès trong tam giác, tính chất đường phân giác của tam giác								1/3c Câu 16 c 1,0đ	1,0
7	Tam giác đồng dạng	Tam giác đồng dạng				1/3c Câu 16a 1,0đ		1/3c Câu 16b 1,0đ			2,0
Tổng: Số câu Điểm			6 1.5		5 1.25	2+1/3c 3,5		2+1/3c 2,25		1+1/3c 1,5	17 10
Tỉ lệ %			15%		47,5%		22,5%		15%		100%
Tỉ lệ chung			62,5%				30 37,5%				100%

4. Bảng đặc tả đề thi cuối học kì 2 lớp 8 KNTT

TT	Chương/ Chủ đề	Nội dung/Đơn vị kiến thức	Mức độ đánh giá	Số câu hỏi theo mức độ nhận thức
			Mức độ đánh giá	Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
			Thông hiểu: – Mô tả được phương trình bậc nhất một ẩn và cách giải		2 – TN 0,5đ
1	Phương trình		- Vận dụng:-Giải được phương trình bậc nhất một ẩn. - Giải quyết được một số vấn đề thực tiễn *(đơn giản, quen thuộc)* gắn với phương trình bậc nhất (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí, các bài toán liên quan đến Hoáhọc,...).		1-TL 1,5 đ
			Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn *(phức hợp, không quen thuộc)* gắn với phương trình bậc nhất.				1 -TL 0,5đ
2	Bất phương trình bậc nhất một ẩn	*Bất đẳng thức. Bất phương* *trình* *bậc nhất một ẩn*	Nhận biết – Nhận biết được thứ tự trên tập hợp các số thực.
			– Nhận biết được bất đẳn gthức.
			– Nhận biết được khái niệm bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất mộtẩn.	2 - TN 0,5đ
			Thông hiểu – Mô tả được một số tính chất cơ bản của bất đẳng thức (tính chất bắc cầu; liên hệ giữa thứ tự và phép cộng, phép nhân).
			– Giải được bất phương trình bậc nhất một ẩn.			1- TL 1,0đ
3	Hàm số và đồ thị	*Hàm số bậc nhất* *y = ax + b* (a ¹ 0) *và đồ thị. Hệ số góc của đường thẳng y = ax + b* (a ¹ 0).	Nhận biết: – Nhận biết được khái niệm hệ số góc của đường thẳng y = ax + b (a ¹ 0).	2 – TN 0,5 đ
			Thông hiểu: – Thiết lập được bảng giá trị của hàm số bậc nhất y = ax + b (a ¹ 0). – Sử dụng được hệ số góc của đường thẳng để nhận biết và giải thích được sự cắt nhau hoặc song song của hai đường thẳng cho trước.		2- TN 0,5đ
			Vận dụng: – Vẽ được đồ thị của hàm số bậc nhất y = ax + b (a ¹ 0). – Vận dụng được hàm số bậc nhất và đồ thị vào giải quyết một số bài toán thực tiễn *(đơn giản, quen thuộc)* (ví dụ: bài toán về chuyển động đều trong Vật lí,...).
4	Phân tích và xử lí dữ liệu	*Mô tả xác suất của biến cố* *ngẫu nhiên* *trong một số ví dụ đơn giản.* *Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó*	Vận dụng: – Sử dụng được tỉ số để mô tả xác suất của một biến cố ngẫu nhiên trong một số ví dụ đơn giản.		1 TL 0,5đ
5	Các hình khối trong thực tiễn	*Hình hộp chữ nhật và hình lập phương*	*Nhận biết* Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương.
		*Hình hộp chữ nhật và hình lập phương*	*Thông hiểu* – Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của hình hộp chữ nhật, hình lập phương (vídụ: tính thể tích hoặc diện tích xung quanh của một số đồ vật quen thuộc có dạng hình hộp chữ nhật, hình lập phương,...).		1-TN 0,25đ
		*Lăng trụ đứng tam giác,* *lăng* *trụ đứng tứ giác, hình chóp*	*Nhận biết* – Mô tả được hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác , hình chóp (ví dụ: hai mặt đáy là song song; các mặt bên đều là hình chữ nhật, ...).	2 - TN 0,5đ
			*Thông hiểu* – Tạo lập được hình lăng trụ đứng tam giác, hình lăng trụ đứng tứgiác.
			– Tính được diện tích xung quanh, thể tích của hình lăng trụ đứng tam giác,hình lăng trụ đứng tứ giác.		1-TN 0,25đ
			- Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của một lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác (ví dụ: tính thể tích hoặc diện tích xung quanh của một số đồ vật quen thuộc có dạng lăng trụ đứng tam giác, lăng trụ đứng tứgiác,...).
			*Vận dụng* Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của một lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
6	*Định lí Thalès trong tam giác*	*Định lí Thalès trong tam giác*	Nhận biết: – Nhận biết được định nghĩa đường trung bình của tam giác.
			Thông hiểu -Giải thích được tính chất đường trung bình của tam giác(đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó).
			– Giải thích được định lí Thalès trong tam giác (định lí thuận vàđảo).
			– Giải thích được tính chất đường phân giác trong của tamgiác, tính độ dài đoạn thẳng
			Vận dụng: – Tính được độ dài đoạn thẳng bằng cách sử dụng định líThalès.
			Giải quyết được một số vấn đề thực tiễn *(đơn giản, quen thuộc)* gắn với việc vận dụng định lí Thalès (ví dụ: tính khoảng cách giữa hai vịtrí).
			Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với việc vận dụng định lí Thalès				1/3 câu - TL 1,0đ
4 5 4$$ 44	*Tam giác đồng dạng*	*Tam giác đồng dạng*	Thông hiểu – Mô tả được định nghĩa của hai tam giác đồngdạng.
			Giải thích được các trường hợp đồng dạng của hai tam giác, của hai tam giác vuông.		1/3 câu –TL 1,0đ	1/3 câu –TL 1,0đ
			Vận dụng: – Giải quyết được một số vấn đề thực tiễn *(đơn giản, quen thuộc)* gắn với việc vận dụng kiến thức về hai tam giác đồng dạng (ví dụ: tính độ dài đường cao hạ xuống cạnh huyền trong tam giác vuông bằng cách sử dụng mối quan hệ giữa đường cao đó với tích của hai hình chiếu của hai cạnh góc vuông lên cạnh huyền; đo gián tiếp chiều cao của vật; tính khoảng cách giữa hai vị trí trong đó có một vị trí không thể tới được,...).
			Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn *(phức hợp, không quen thuộc)* gắn với việc vận dụng kiến thức về hai tam giác đồng dạng.
Tổng Điểm				6c 1,5đ	7c + 1/3c 4,75	2c+1/3c 2,25	1c+1/3c 1,5đ
Tỉ lệ %				15%	47,5%	22,5%	15%
Tỉ lệ chung				62,5%		37,5%