Đề thi học kì 2 Toán 8 Cánh diều

Đề thi cuối kì 2 Toán 8 Cánh diều có đáp án

1 1.584

Đề thi cuối kì 2 Toán 8 năm 2024 có đáp án

Đề thi học kì 2 Toán 8 Cánh diều có đầy đủ đáp án, thầy cô có thể tham khảo ra đề kiểm tra và làm tài liệu ôn luyện cho các em học sinh. Đây cũng là tài liệu hay giúp các em học sinh ôn tập, làm quen với nhiều dạng đề khác nhau, chuẩn bị cho kì thi cuối học kì 2 Toán 8 sắp tới đạt kết quả cao. Mời các bạn tải về tham khảo toàn bộ đề thi, đáp án, ma trận và bảng đặc tả đề thi.

Để chuẩn bị cho kì thi học kì 2 sắp tới, các em học sinh cần thực hành luyện tập để làm quen với nhiều dạng đề khác nhau cũng như nắm được các dạng bài thường có trong đề thi. Chuyên mục Đề thi học kì 2 lớp 8 trên VnDoc tổng hợp đề thi tất cả các môn, là tài liệu hay cho các em học sinh ôn tập và luyện đề.

1. Đề thi cuối kì 2 Toán 8 Cánh diều

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Mỗi câu lạc bộ tại trường Trung học Sao Mai có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây:

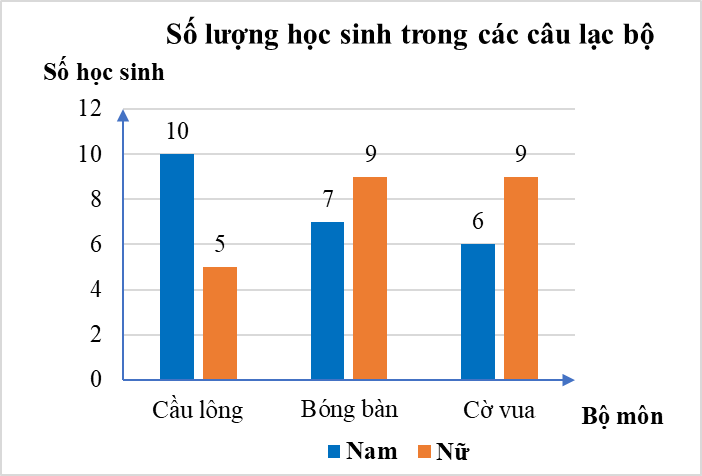
Biết trong biểu đồ, dữ liệu thống kê của một câu lạc bộ chưa chính xác, đó là

A. Cầu lông.

B. Bóng bàn.

C. Cờ vua.

D. Không có dữ liệu chưa chính xác trong biểu đồ.

Câu 2: Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?

A. 1

B. $\frac{1}{4}$

C. $\frac{1}{5}$

D. 5

Câu 3. Phương trình nào sau đây là phương trình bậc nhất một ẩn?

A. 0x + 5 = 0.

B. x² - 4 = 0.

C. $\frac{1}{2} x -3 = 0$

D. x³ - x + 2 = 0

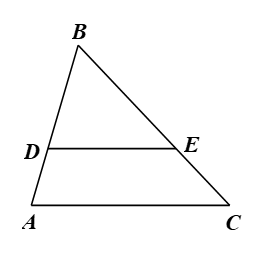
Câu 4. Cho hình vẽ bên, biết DE // AC.

Tỉ số nào sau đây là đúng?

A. BD/AD=BE/BC.

B. BD/AD=BE/EC.

C. DE/AC=BC/BE.

D. AD/AB=BC/EC.

Câu 5. Cho các mệnh đề sau:

(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

(II) Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

Hãy chọn đáp án đúng:

A. Cả (I) và (II) đều đúng.

B. Chỉ có (II) đúng.

C. Chỉ có (I) đúng.

D. Cả (I) và (II) đều sai.

Câu 6. Cho ∆RSK và ∆RSK có RSPQ=RKPM=SKQM, khi đó ta có

A. ∆RSK ᔕ ∆MPQ.

B. ∆RSK ᔕ ∆PQM.

C. ∆RSK ᔕ ∆QPM.

D. ∆RSK ᔕ ∆QMP.

PHẦN II. TỰ LUẬN (7,0 điểm)

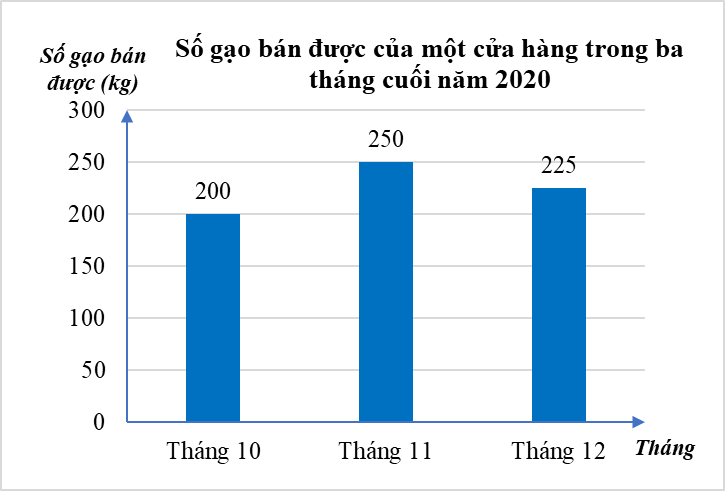
Bài 1. (1,0 điểm) Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.

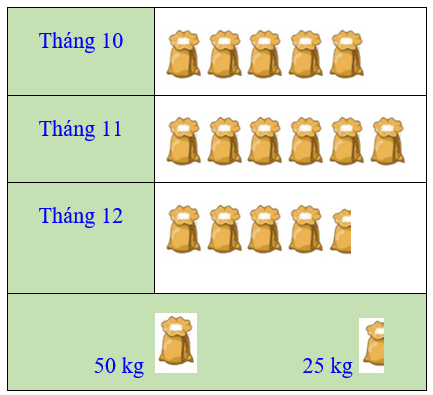
a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 theo mẫu sau:

Năm	Tháng 10	Tháng 11	Tháng 12
Số gạo bán được (kg)

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.

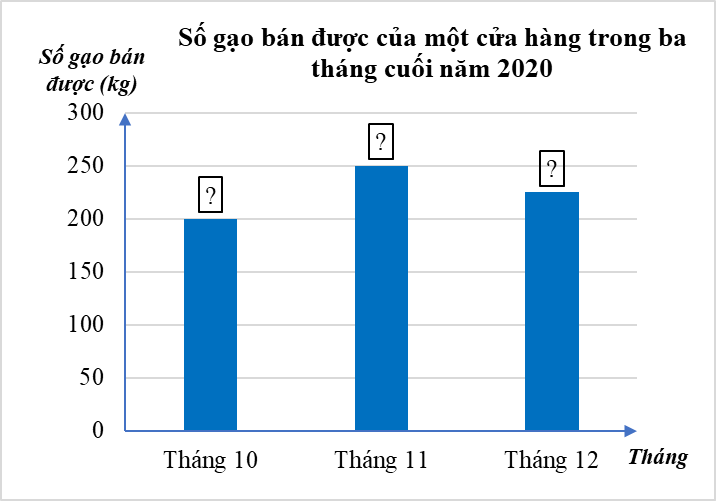
Bài 2. (1,5 điểm) Hiệu hai số là 12. Nếu chia số bé cho 7 và lớn cho 5 thì thương thứ nhất lớn hơn thương thứ hai là 4 đơn vị. Tìm hai số đó.

Bài 3. (1,0 điểm) Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, cô giáo đã chọn ra 10 học sinh gồm 4 học sinh nữ nữ là Hoa; Mai; Linh; My; 6 học sinh nam là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm 10 học sinh tập múa trên.

a) Tìm số phần tử của tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra.

b. Tính xác suất của các biến cố “Học sinh được chọn ra là học sinh nam”

Bài 4. (1,0 điểm)

Giải bài toán bằng cách lập phương trình

Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.

Bài 5. (2,0 điểm)

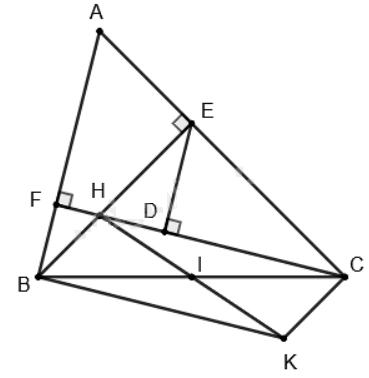
Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H

a) Chứng minh $\Delta ABE\backsim \Delta ACF$

b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh $H{E^2} = HD.HC$ .

c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.

Bài 6. (0,5 điểm)

Cho ba số thực a, b, c khác 2 thỏa mãn a + b + c = 6. Tính giá trị của biểu thức:

$M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}$

−−−−−HẾT−−−−−

2. Đáp án Đề thi cuối kì 2 Toán 8 Cánh diều

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6
Đáp án	B	C	C	B	C	A

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm)

a) Ta có bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 như sau:

Năm	Tháng 10	Tháng 11	Tháng 12
Số gạo bán được (kg)	200	250	225

b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là:

Bài 2. (1,5 điểm)

Gọi số bé là x (x∈ℕ*).

Số lớn là x + 12.

Chia số bé cho 7 ta được thương là $\frac{x}{7}$ .

Chia số lớn cho 5 ta được thương là $\frac{x+12}{5}$ .

Vì thương thứ nhất lớn hơn thương thứ hai 4 đơn vị nên ta có phương trình:

$\frac{x+12}{5} - \frac{x}{7} = 4$

7(x + 12) - 5x = 140

7x + 84 - 5x = 140

2x = 56

x = 28

Vậy số bé là 28; số lớn là: 28 + 12 = 40.

Bài 3. (1,0 điểm)

a) Tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra là :

M = {Hoa; Mai; Linh; My; Cường; Hường; Mỹ; Kiên; Phúc; Hoàng}.

Số phần tử của tập hợp M là 10.

b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nam” đó là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng.

Vì thế xác suất của biến cố đó là $\frac{6}{10} = \frac{3}{5}$ .

Bài 4. (1,0 điểm)

Gọi năng suất của tổ sản suất là x (chiếc thảm) ( $x \in N*$ ).

Khi đó năng suất thực tế của tổ là: $x + 20\% x = 120\% x = 1,2x$

Số thảm tổ cần dệt là: 20x (chiếc thảm)

Số thảm tổ làm được là: $18.1,2x = 21,6x$ .

Vì tổ còn làm thêm được 24 chiếc thảm so với số thảm được giao nên ta có phương trình:

$20x + 24 = 21,6x$

Giải phương trình ta được $x = 15$ (TM)

Vậy số thảm thực tế tổ sản xuất làm được là: $21,6.15 = 324$ chiếc thảm.

Bài 5. (2 điểm)

a) Xét $\Delta ABE$ và $\Delta ACF$ có:

$\widehat {BEA} = \widehat {CFA} = {90^0}$

$\widehat A$ chung

suy ra $\Delta ABE\backsim \Delta ACF$ (g.g) (đpcm)

b) Ta có DE // AB nên $\widehat {HED} = \widehat {ABE}$ (hai góc so le trong)

$\widehat {ACF} = \widehat {ABE}$ (do $\Delta ABE\backsim \Delta ACF$ )

suy ra $\widehat {ACF} = \widehat {HED}$

Xét $\Delta HED$ và $\Delta HCE$ có:

$\widehat H$ chung

$\widehat {ACF} = \widehat {HED}$

suy ra $\Delta HED\backsim \Delta HCE$ (g.g)

suy ra $\frac{{HE}}{{HC}} = \frac{{HD}}{{HE}}$ hay $H{E^2} = HD.HC$ (đpcm)

c) Xét tứ giác BHCK có:

BH // CK (gt)

BK // HC (gt)

suy ra BHCK là hình bình hành.

Suy ra BC và HK cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của BC nên I cũng là trung điểm của HK hay H, I, K thẳng hàng (đpcm).

Bài 6. (0.5 điểm)

Ta có: $M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}$

$= \frac{{{{\left( {a - 2} \right)}^3} + {{\left( {b - 2} \right)}^3} + {{\left( {c - 2} \right)}^3}}}{{\left( {a - 2} \right)\left( {b - 2} \right)\left( {c - 2} \right)}}$

Đặt a – 2 = x, b – 2 = y, c – 2 = z, biểu thức $M$ trở thành:

$M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}$

Mặt khác, từ a + b + c = 6 suy ra $\left( {a - 2} \right) + \left( {b - 2} \right) + \left( {c - 2} \right) = 0$ hay $x + y + z = 0$ .

Suy ra

$\begin{array}{l}x + y = - z\\{\left( {x + y} \right)^3} = {\left( { - z} \right)^3}\\{x^3} + {y^3} + 3xy\left( {x + y} \right) = - {z^3}\\{x^3} + {y^3} + 3xy\left( { - z} \right) = - {z^3}\\{x^3} + {y^3} + {z^3} = 3xyz\end{array}$