Bộ 10 đề thi học kì 2 lớp 8 môn Toán năm 2023

Đề kiểm tra học kì 2 Toán 8 có đáp án

Bộ đề kiểm tra Toán 8 học kì 2

1. Đề thi Toán lớp 8 học kì 2 năm số 1
2. Đề thi học kì 2 lớp 8 môn Toán số 2
3. Đề thi học kì 2 lớp 8 Môn khác

Bộ đề thi học kì 2 lớp 8 môn Toán năm 2024 do thư viện đề thi VnDoc.com sưu tầm. Đây là đề thi học kì 2 Toán 8 dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh trong quá trình ôn tập học kì 2 lớp 8. Chúc các bạn học tốt, mời các bạn cùng tham khảo

Kỳ thi cuối kì 2 đang đến gần, để giúp các em học sinh ôn thi tốt hơn, VnDoc đã sưu tầm và biên soạn bộ đề thi học kì 2 lớp 8 môn Toán rất kỹ lưỡng, có đáp án kèm theo. Để tải về ôn thi, làm tài liệu tham khảo, mời các bạn kích tham khảo Đề thi Toán lớp 8 học kì 2 có đáp án dưới đây.

1. Đề thi Toán lớp 8 học kì 2 năm số 1

Bài 1: Giải các phương trình dưới đây:

a, 3(x - 17) - 2(x - 17) = 203	b, $\frac{5}{{x - 6}} + \frac{4}{{x + 6}} = \frac{{x - 8}}{{{x^2} - 36}}$ $\frac{5}{{x - 6}} + \frac{4}{{x + 6}} = \frac{{x - 8}}{{{x^2} - 36}}$
c, (x - 1)(x² - 3x + 2) = 0	d, 4(2x + 3) - 5\|3x - 1\| = 12

Bài 2: Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số

a, $\frac{{x - 5}}{2} - \frac{{x - 3}}{6} < \frac{{2x + 1}}{3}$ $\frac{{x - 5}}{2} - \frac{{x - 3}}{6} < \frac{{2x + 1}}{3}$

b, 6x + 2 ≥ 7x + 1

Bài 3: Giải bài toán bằng cách lập phương trình

Một mảnh đất hình chữ nhật có diện tích là 720m². Nếu tăng chiều rộng lên 6m và giảm chiều dài đi 4m thì diện tích mảnh đất không đổi. Tính chu vi mảnh đất lúc ban đầu.

Bài 4: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ đường cao AH

a, Chứng minh tam giác ABC đồng dạng với tam giác HBA

b, Chứng minh AH² = HB.HC

c, Tính độ dài các cạnh BC, AH

d, Tia phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của hai tam giác ACD và CEH

Bài 5: Cho 2x² + 2y² = 5xy và 0 < x < y. Tính giá trị của $E = \frac{{x + y}}{{x - y}}$ $E = \frac{{x + y}}{{x - y}}$

Đáp án Đề thi Toán lớp 8 học kì 2 số 1

Bài 1:

a, S = {2020}

b, S = {- 7}

c, S = {1; 2}

d, $S = \left\{ {\frac{{ - 7}}{{23}};\frac{{17}}{7}} \right\}$ $S = \left\{ {\frac{{ - 7}}{{23}};\frac{{17}}{7}} \right\}$

Bài 2:

a, S = {x| x > - 7}

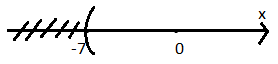
Đề thi Toán lớp 8 học kì 2 năm học 2019 - 2020 - Đề số 2

b, S = {x| x ≤ 1}

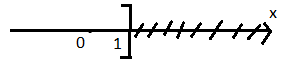
Đề thi Toán lớp 8 học kì 2 năm học 2019 - 2020 - Đề số 2

Bài 3:

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m, x > 0)

Chiều dài của mảnh đất hình chữ nhật là: $\frac{{720}}{x}$ $\frac{{720}}{x}$(m)

Chiều rộng mới của mảnh đất hình chữ nhật là x + 6 (m)

Chiều dài mới của mảnh đất hình chữ nhật là $\frac{{720}}{x} - 4$ $\frac{{720}}{x} - 4$(m)

Theo đề bài, ta có phương trình: $\left( {x + 6} \right)\left( {\frac{{720}}{x} - 4} \right) = 720$ $\left( {x + 6} \right)\left( {\frac{{720}}{x} - 4} \right) = 720$

⇔ 720 - 4x + $\frac{4320}{x}$ $\frac{4320}{x}$ - 24 = 720

⇔ 720x - 4x² + 4320 - 24x - 720x = 0

⇔ -4x² -24x + 4320 = 0

⇔ (x - 30)(x + 36) = 0

Vậy x = 30 (thỏa mãn)

Chiều rộng của mảnh vườn hình chữ nhật là 24m, chiều dài của mảnh vườn hình chữ nhật là 30m

Chu vi của mảnh đất hình chữ nhật là: (24 + 30).2 = 108m

Bài 4:

(Học sinh tự vẽ hình)

a, Tam giác vuông ABC và tam giác vuông HBA có góc $\widehat {ABC}$ $\widehat {ABC}$ chung nên hai tam giác đồng dạng với nhau theo trường hợp góc – góc

b, Chứng minh $\Delta HAC\sim\Delta HBA \Rightarrow \frac{{HA}}{{HB}} = \frac{{HC}}{{HA}} \Rightarrow H{A^2} = HB.HC$ $\Delta HAC\sim\Delta HBA \Rightarrow \frac{{HA}}{{HB}} = \frac{{HC}}{{HA}} \Rightarrow H{A^2} = HB.HC$

c, Áp dụng định lý Pytago cho tam giác vuông ABC để tính được BC = 10cm

Từ câu a $\Delta ABC\sim\Delta HBA \Rightarrow \frac{{AC}}{{HA}} = \frac{{BC}}{{BA}} \Rightarrow HA.BC = AC.BA$ $\Delta ABC\sim\Delta HBA \Rightarrow \frac{{AC}}{{HA}} = \frac{{BC}}{{BA}} \Rightarrow HA.BC = AC.BA$. Suy ra tính được HA = 4,8cm

d, Áp dụng định lý Pytago cho tam giác vuông AHC để tính được CH = 6,4cm

Chứng minh được tam giác CAD đồng dạng với tam giác CHE $\Rightarrow \frac{{CA}}{{CH}} = \frac{{AD}}{{HE}}$ $\Rightarrow \frac{{CA}}{{CH}} = \frac{{AD}}{{HE}}$

Tính ra được tỉ số $\frac{{AD}}{{HE}} = \frac{8}{{6,4}} = \frac{5}{4}$ $\frac{{AD}}{{HE}} = \frac{8}{{6,4}} = \frac{5}{4}$

Có ${S_{\Delta ACD}} = \frac{1}{2}.AC.AD$ ${S_{\Delta ACD}} = \frac{1}{2}.AC.AD$ và ${S_{\Delta CEH}} = \frac{1}{2}.CH.EH$ ${S_{\Delta CEH}} = \frac{1}{2}.CH.EH$

Suy ra $\frac{{{S_{\Delta ACD}}}}{{{S_{\Delta CEH}}}} = \frac{{AC.AD}}{{CH.EH}} = \frac{{AC}}{{CH}}.\frac{{AD}}{{EH}} = \frac{5}{4}.\frac{5}{4} = \frac{{25}}{{16}}$ $\frac{{{S_{\Delta ACD}}}}{{{S_{\Delta CEH}}}} = \frac{{AC.AD}}{{CH.EH}} = \frac{{AC}}{{CH}}.\frac{{AD}}{{EH}} = \frac{5}{4}.\frac{5}{4} = \frac{{25}}{{16}}$

Bài 5:

Có 2x² + 2y² = 5xy

⇔ 2x² - 2y² - 5xy =0

⇔ 2x² - 4xy - xy + 2y² = 0

⇔ 2x(x - 2y) - y(x - 2y) = 0

⇔ (x - 2y)(2x - y) = 0

$\Leftrightarrow \left[ \begin{array}{l}x - 2y = 0\\2x - y = 0\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x - 2y = 0\\2x - y = 0\end{array} \right.$

Trường hợp 1: Với x – 2y = 0 hay x = 2y thì

$E = \frac{{2y + y}}{{2y - y}} = \frac{{3y}}{y} = 3$ $E = \frac{{2y + y}}{{2y - y}} = \frac{{3y}}{y} = 3$ (loại do 0 < x < y nên $E = \frac{{x + y}}{{x - y}} < 0$ $E = \frac{{x + y}}{{x - y}} < 0$)

Trường hợp 2: Với 2x – y = 0 hay 2x = y thì

$E = \frac{{x + 2x}}{{x - 2x}} = \frac{{3x}}{{ - x}} = - 3$ $E = \frac{{x + 2x}}{{x - 2x}} = \frac{{3x}}{{ - x}} = - 3$(tm)

Vậy E = -3

2. Đề thi học kì 2 lớp 8 môn Toán số 2

Bài 1 (3,5 điểm). Giải các phương trình và bất phương trình sau:

$a)\ 3x - 11 = x + 7$ $a)\ 3x - 11 = x + 7$

$b)\ 2x(x - 3) = x - 3$ $b)\ 2x(x - 3) = x - 3$

$\text { c) } \frac{x+2}{x-2}-\frac{5}{x}=\frac{8}{x^{2}-2 x}$ $\text { c) } \frac{x+2}{x-2}-\frac{5}{x}=\frac{8}{x^{2}-2 x}$

$\text { d) } \frac{2 x+1}{4}-\frac{x-5}{3} \leq \frac{4 x-1}{12}+2$ $\text { d) } \frac{2 x+1}{4}-\frac{x-5}{3} \leq \frac{4 x-1}{12}+2$

Bài 2 (2,0 điểm). Giải bài toán bằng cách lập phương trình

Một xe máy khởi hành từ A để đi đến B với vận tốc 30km/h. Sau khi xe máy đi được 20 phút, trên cùng tuyến đường đó, một ô tô khởi hành từ B để đi đến A với vận tốc 45km/h. Biết quãng đường AB dài 90 km. Hỏi sau bao lâu kể từ lúc ô tô khởi hành thì hai xe gặp nhau.

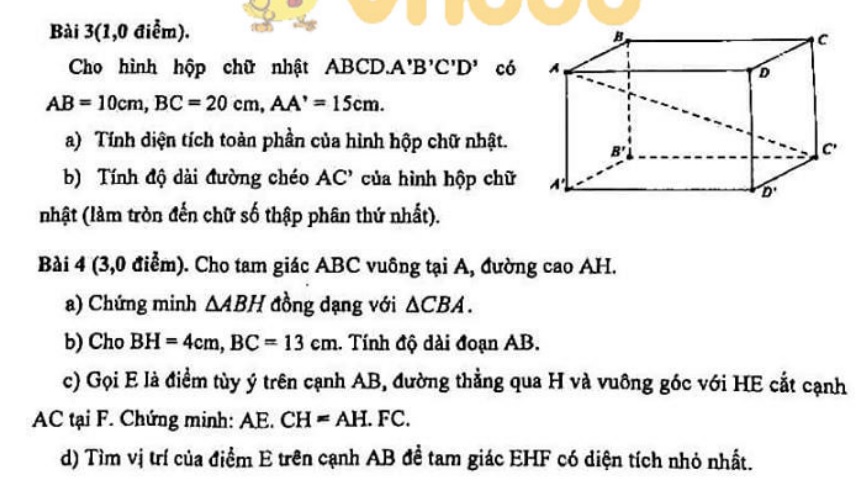
Bộ đề thi học kì 2 lớp 8 môn Toán

Mời các bạn tải về để xem toàn bộ 10 đề thi và đáp án

VnDoc đã giới thiệu tới các bạn Bộ đề thi học kì 2 lớp 8 môn Toán. Với tài liệu này sẽ là tài liệu hay cho các bạn tham khảo, tự đánh giá năng lực của mình đồng thời biết phân bổ thời gian làm bài. Chúc các bạn học sinh ôn thi tốt và nhớ thường xuyên ghé thăm VnDoc để cập nhật những tài liệu hay, bổ ích khác nhé

3. Đề thi học kì 2 lớp 8 Môn khác

............................................

Ngoài Bộ đề thi học kì 2 lớp 8 môn Toán. Để chuẩn bị cho kì thi học kì 2 lớp 8 sắp tới, các em học sinh cần ôn tập theo đề cương, bên cạnh đó cần thực hành luyện đề để làm quen với nhiều dạng đề khác nhau cũng như nắm được cấu trúc đề thi. Chuyên mục Đề thi học kì 2 lớp 8 trên VnDoc tổng hợp đề thi của tất cả các môn, là tài liệu phong phú và hữu ích cho các em ôn tập và luyện đề. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời thầy cô và các em tham khảo.

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Chia sẻ, đánh giá bài viết

121

72.519

Bài trước

Bài sau