Bài tập Đường trung bình của tam giác lớp 8
Chuyên đề Toán học lớp 8: Đường trung bình của tam giác được VnDoc sưu tầm và đăng tải gồm lý thuyết và các dạng bài tập liên quan đến đường trung bình của tam giác của hình thang. Hy vọng với tài liệu này sẽ giúp ích cho các em học tốt môn Toán lớp 8. Dưới đây là nội dung chi tiết mời các em tham khảo
Chuyên đề: Đường trung bình của tam giác
A. Đường trung bình của tam giác
– Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
– Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Δ ABC có D là trung điểm của AB, E là trung điểm của AC thì DE // BC và 
\(\text{DE}=\frac{1}{2}\text{BC}\)
– Chú ý: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
Ví dụ 1: Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4 cm. Tính độ dài MN.
Lời giải:
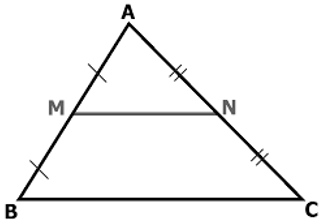
Xét tam giác ABC có: M là trung điểm của AB (gt), N là trung điểm của AC (gt)
⇒ MN là đường trung bình của Δ ABC (định lý)
Áp dụng định lý 2, ta có \(\text{MN}=\frac{1}{2}\text{BC}\)
⇒ \(\text{MN}=\frac{1}{2}\text{BC}=\frac{1}{2}.4 = 2\) (cm)
B. Các dạng toán
1. Dạng 1: Dựa vào đường trung bình của tam giác, tính độ dài các cạnh.
Ví dụ 2: Cho tam giác ABC có AB = 6 cm, AC = 10 cm, BC = 14 cm. Gọi D, E, F lần lượt là trung điểm của AB, AC và BC. Tính độ dài các cạnh DE, DF và EF.
Lời giải:
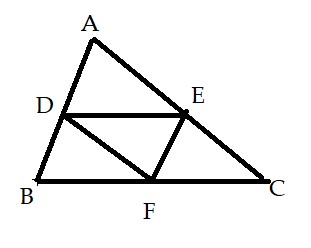
+ Xét tam giác ABC có D là trung điểm của AB, E là trung điểm của AC
Suy ra DE là đường trung bình của tam giác ABC \(\Rightarrow\text{DE}=\frac{1}{2}BC=\frac{1}{2}.14=7\) cm
+ Xét tam giác ABC có D là trung điểm của AB, F là trung điểm của BC
Suy ra DF là đường trung bình của tam giác ABC \(\Rightarrow\text{DF}=\frac{1}{2}AC=\frac{1}{2}.10=5\) cm
+ Xét tam giác ABC có E là trung điểm của AC, F là trung điểm của BC
Suy ra EF là đường trung bình của tam giác ABC \(\Rightarrow\text{EF}=\frac{1}{2}AB=\frac{1}{2}.6=3\) cm
2. Dạng 2: Chứng minh đường trung bình
Ví dụ 3: Cho tam giác ABC có I, J lần lượt là trung điểm của các cạnh AB, BC. Chứng minh IJ là đường trung bình của tam giác ABC.
Lời giải:
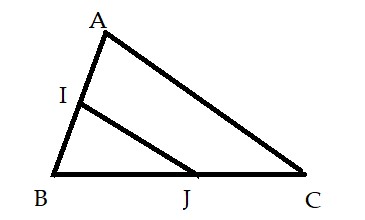
Xét tam giác ABC có:
I là trung điểm của AB
J là trung điểm của BC
Suy ra IJ là đường trung bình của tam giác ABC (định lý) (đpcm)
3. Dạng 3: Chứng minh các đường thẳng song song với nhau
Ví dụ 4: Cho tam giác ABC có I, J lần lượt là trung điểm của các cạnh AB, BC. Chứng minh tứ giác AIJC là hình thang.
Lời giải:
+ Xét tam giác ABC có:
I là trung điểm của AB
J là trung điểm của BC
Suy ra IJ là đường trung bình của tam giác ABC (định lý)
Suy ra IJ // AC (định lý)
+ Xét tứ giác AIJC có: IJ // AC (cmt)
Suy ra tứ giác AIJC là hình thang (định nghĩa)
C. Bài tập trắc nghiệm và tự luận Toán 8
I. Bài tập trắc nghiệm
Bài 1: Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Phát biểu nào sau đây sai?
A. DE là đường trung bình của tam giác ABC.
B. DE song song với BC.
C. DECB là hình thang cân.
D. DE có độ dài bằng nửa BC.
Hướng dẫn:
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE // BC và \(\text{DE}=\frac{1}{2}\text{BC}\)
+ Hình thang cân là hình thang có hai góc kề một cạnh bằng nhau và hai cạnh bên bằng nhau nhưng bài toán này hai góc kề một cạnh đấy không bằng nhau
→ Đáp án C sai.
Chọn đáp án C.
Bài 2: Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4 cm. Biết đường cao AH = 6 cm. Diện tích của tam giác ABC là?
| A. S = 24 cm2 | B. S = 16 cm2 | C. S = 48 cm2 | D. S = 32 cm2 |
Hướng dẫn:
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE//BC và DE = \(\frac{1}{2}\)BC ⇒ BC = 2DE = 2.4 = 8 cm
Khi đó ta có: S = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\).6.8 = 24 cm2
Chọn đáp án A.
Bài 3: Chọn phát biểu đúng
A. Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên của hình thoi.
B. Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh đối của hình thoi.
C. Đường trung bình của hình thang thì song song với hai đáy và bằng tổng hai hai đáy.
D. Một hình thang có thể có một hoặc nhiều đường trung bình.
Hướng dẫn:
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
→ Đáp án A đúng.
+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng của hai đáy.
+ Một hình thang thì chỉ có 1 đường trung bình duy nhất.
Chọn đáp án A.
II. Bài tập tự luận
Tải file để xem thêm bài tập và đáp án chi tiết!
