Trường hợp đồng dạng thứ ba
VnDoc xin giới thiệu Chuyên đề Toán học lớp 8: Trường hợp đồng dạng thứ ba. Nội dung gồm lý thuyết và bài tập trắc nghiệm kèm theo giúp các em nắm chắc kiến thức áp dụng tốt vào làm bài tập tương ưng. Chúc các em học tốt, tham khảo chi tiết dưới đây
Chuyên đề Trường hợp đồng dạng thứ ba của tam giác
A. Lý thuyết Trường hợp đồng dạng thứ ba
I. Định lý:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Nếu 
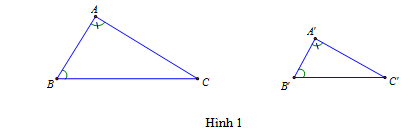
\(\Delta ABC\) và \(\Delta A'B'C'\) có có \(\widehat A = \widehat {A'}\) và \(\widehat B = \widehat {B'}\) (h.1) thì \(\Delta ABC \backsim \Delta A'B'C'\,\left( {g.g} \right).\)
II. Các dạng toán thường gặp
Dạng 1: Sử dụng tam giác đồng dạng để tính toán
Phương pháp:
Ta sử dụng các tỉ lệ cạnh và các góc bằng nhau của hai tam giác đồng dạng để tính toán.
Dạng 2: Chứng minh hai tam giác đồng dạng và các hệ thức liên quan.
Phương pháp:
Ta sử dụng định lý: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
B. Giải bài tập Toán 8 bài 7
- Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba
- Giải bài tập SBT Toán 8 bài 7: Trường hợp đồng dạng thứ ba (g.g)
C. Trắc nghiệm Trường hợp đồng dạng thứ ba
Như vậy VnDoc đã chia sẻ tới các bạn Lý thuyết Toán 8 Trường hợp đồng dạng thứ ba. Hy vọng tài liệu sẽ giúp các em nắm chắc kiến thức từ đó vận dụng tốt để giải bài tập Toán lớp 8 hiệu quả. Chúc các em học tốt.
Ngoài Lý thuyết Toán 8 Trường hợp đồng dạng thứ ba, các bạn học sinh có thể tham khảo thêm tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Trắc nghiệm Toán 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.
