Phương trình đưa được về dạng ax + b = 0

Chuyên đề Toán học lớp 8: Phương trình đưa được về dạng ax + b = 0 được biên soạn nhằm hệ thống hóa những kiến thức trọng tâm và nền tảng của dạng toán quan trọng này. Tài liệu tổng hợp đầy đủ lý thuyết cơ bản, giúp học sinh hiểu rõ cách biến đổi phương trình về dạng quen thuộc để tìm nghiệm chính xác. Bên cạnh phần lý thuyết là các ví dụ minh họa cụ thể, trình bày từng bước rõ ràng, kèm theo hệ thống bài tập có hướng dẫn giải chi tiết để các em luyện tập và củng cố kiến thức. Thông qua việc học và thực hành với chuyên đề này, học sinh sẽ nâng cao kỹ năng giải Toán 8, rèn luyện tư duy logic và tự tin hơn khi làm bài kiểm tra. Dưới đây là nội dung chi tiết, mời các em cùng tham khảo.

Để ôn tập hiệu quả dạng bài tập này, mời các bạn tham khảo thêm:

Bài tập Toán lớp 8: Phương trình đưa được về dạng ax+b=0

A. Lý thuyết Phương trình đưa được về dạng ax + b = 0

1. Cách giải

Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:

Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có)

Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c.

Bước 3: Tìm x

Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:

0x = c thì phương trình vô nghiệm

0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm S = R.

Ví dụ 1: Giải phương trình 2x - (3 - 2x) = 3x + 1

Hướng dẫn:

Ta có 2x - (3 - 2x) = 3x + 1 ⇔ 2x - 3 + 2x = 3x + 1

⇔ 4x - 3x = 1 + 3 ⇔ x = 4.

Vậy phương trình đã cho có tập nghiệm là S = {4}.

Ví dụ 2: Giải phương trình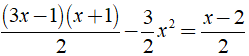

Hướng dẫn:

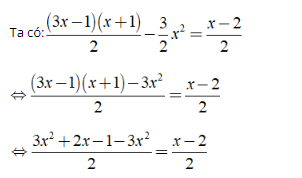
⇔ 2x - 1 = x - 2 ⇔ x = - 1.

Vậy phương trình đã cho có tập nghiệm là S = { - 1 }.

Ví dụ 3: Giải phương trình

Hướng dẫn:

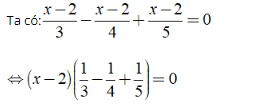
⇔ ( x - 2 )17/60 = 0 ⇔ x - 2 = 0 ⇔ x = 2.

Vậy phương trình có tập nghiệm là S = { 2 }.

Ví dụ 4: Giải phương trình x + 1 = x - 1.

Hướng dẫn:

Ta có x + 1 = x - 1 ⇔ x - x = - 1 - 1 ⇔ 0x = - 2.

Vậy phương trình đã cho vô nghiệm.

Ví dụ 5: Giải phương trình x - 3 = x - 3.

Hướng dẫn:

Ta có: x - 3 = x - 3 ⇔ x - x = - 3 + 3 ⇔ 0x = 0.

Vậy phương trình đã cho vô số nghiệm.

B. Trắc nghiệm & Tự luận Phương trình đưa được về dạng ax + b = 0

I. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình 4(x - 1) - (x + 2) = - x là?

A. x = 2. B. x = 3/2. C. x = 1. D. x = - 1.

Ta có: 4(x - 1) - (x + 2) = - x

⇔ 4x - 4 - x - 2 = - x

⇔ 4x - x + x = 2 + 4 ⇔ 4x = 6 ⇔ x = 3/2.

Vậy phương trình đã cho có nghiệm là x = 3/2.

Chọn đáp án B.

Bài 2: Nghiệm của phương trình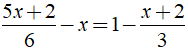 là?

A. x = 0. B. x = 1. C. x = 2. D. x = 3.

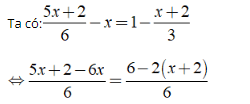
⇔ 5x + 2 - 6x = 6 - 2x - 4

⇔ 5x - 6x + 2x = 6 - 4 - 2 ⇔ x = 0

Vậy phương trình đã cho có nghiệm là x = 0.

Chọn đáp án A.

Bài 3: Tập nghiệm của phương trình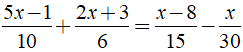 là?

A. S = {4/3}. B. S = {- 3/4} C. S = {- 7/6}. D. S = {- 6/7}.

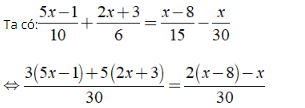
⇔ 15x - 3 + 10x + 15 = 2x - 16 - x

⇔ 25x - 2x + x = - 16 - 15 + 3

⇔ 24x = - 28 ⇔ x = - 7/6.

Vậy phương trình đã cho có tập nghiệm là S = { - 7/6 }.

Chọn đáp án C.

Bài 4: Nghiệm của phương trình - 10(2,3 - 3x) = 5(3x + 1) là?

A. x = 1,2 B. x = - 1,2 C. x = - 28/15 D. x = 28/15

Ta có: - 10(2,3 - 3x) = 5(3x + 1)

⇔ - 23 + 30x = 15x + 5

⇔ 30x - 15x = 5 + 23

⇔ 15x = 28 ⇔ x = 28/15.

Vậy phương trình đã cho có nghiệm là x = 28/15

Chọn đáp án D.

Bài 5: Nghiệm của phương trình là?

A. x = - 30/31. B. x = 30/31. C. x = - 1. D. x = - 31/30.

Hướng dẫn: Ta có:

⇔ 15x + 15 + 5 - 20 = 30x + 10 + 16x + 20

⇔ 31x = - 30 ⇔ x = - 30/31.

Vậy phương trình đã cho có nghiệm là x = - 30/31.

Chọn đáp án A.

II. Bài tập tự luận

Bài 1: Giải các phương trình sau:

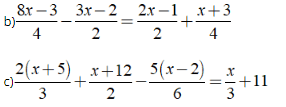
Hướng dẫn:

a) Ta có: 5(x - 3) - 4 = 2(x - 1) + 7

⇔ 5x - 15 - 4 = 2x - 2 + 7

⇔ 5x - 2x = 15 + 4 + 2 - 7

⇔ 3x = 14 ⇔ x = 14/3

Vậy phương trình đã cho có nghiệm là x = 14/3.

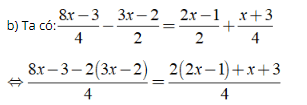
⇔ 8x - 3 - 6x + 4 = 4x - 2 + x + 3

⇔ 5x - 2x = 6 - 6 ⇔ x = 0

Vậy phương trình đã cho có nghiệm là x = 0.

⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66

⇔ 0x = 0

⇒ Phương trình đã cho vô số nghiệm.

Vậy phương trình đã cho vô số nghiệm.

Bài 2: Giải các phương trình sau

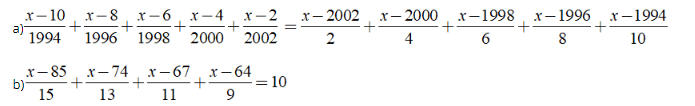
Hướng dẫn:

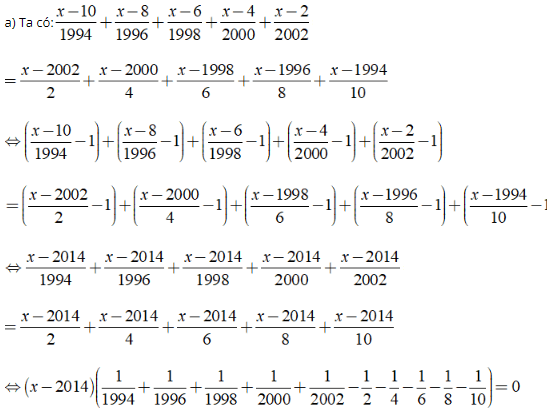
⇒ x - 2014 = 0 ⇔ x = 2014.

Vậy phương trình đã cho có nghiệm là x = 2014.

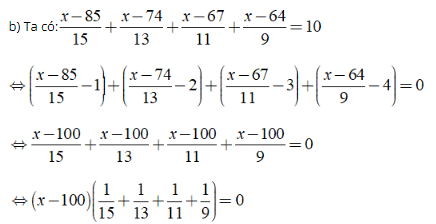
⇒ x - 100 = 0 ⇔ x = 100.

Vậy phương trình đã cho có nghiệm là x = 100.

......................................

Phương trình đưa được về dạng ax + b = 0 được VnDoc chia sẻ trên đây. Hy vọng thông qua tài liệu này các em sẽ nắm chắc lý thuyết, áp dụng vào trả lời các câu hỏi cuối bài, từ đó học tốt môn Toán lớp 8. Chúc các em học tốt.

Ngoài lý thuyết môn Toán học 8: Phương trình đưa được về dạng ax + b = 0, mời các bạn tham khảo thêm Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.

	Đặt câu hỏi về học tập, giáo dục, giải bài tập của bạn tại chuyên mục Hỏi đáp của VnDoc
Hỏi - Đáp	Truy cập ngay: Hỏi - Đáp học tập