Diện tích hình thang
Chuyên đề Toán học lớp 8: Diện tích hình thang được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Diện tích hình thang
A. Lý thuyết
1. Công thức diện tích của hình thang
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
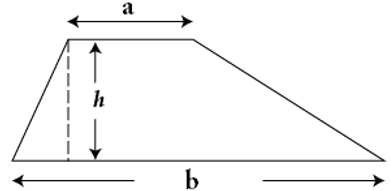
Ta có: S = 1/2(a + b).h
Lý thuyết tính diện tích hình thang: Muốn tính diện tích hình thang ta cộng tổng hai đáy rồi nhân với chiều cao, sau đó chia đôi.
Ví dụ: Cho hình thang ABCD (AB//CD) có AB = 3cm; CD = 5cm, chiều cao hình thang là h = 4cm. Tính diện tích hình thang?
Hướng dẫn:
Diện tích hình thang cần tìm là SABCD = 1/2(AB + CD).h = 1/2( 3 + 5 ).4 = 16cm2
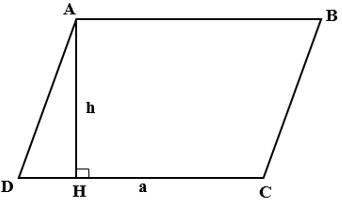
2. Công thức tính diện tích hình bình hành
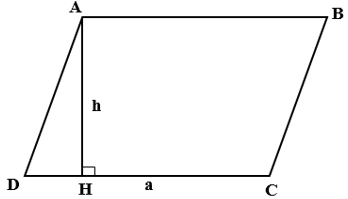
Ta có : S = a.h
Ví dụ: Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 5cm, độ dài đường cao hình bình hành là h = 4cm. Tính diện tích của hình bình hành?
Hướng dẫn:
Diện tích hình hình hành là SABCD = AB.h = 4.5 = 20cm2
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Hình thang có độ dài đáy lần lượt là 2√ 2 cm, 3cm và chiều cao là 3√ 2 cm. Diện tích của hình thang là?
A. 2( 2 + √ 2)cm2.
B. 3(2 + 3/2√ 2)cm2.
C. 3(3 + √ 2)cm2.
D. 3(2 + √ 2 /2)cm2
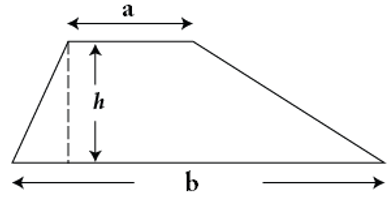
Ta có: S = 1/2(a + b).h
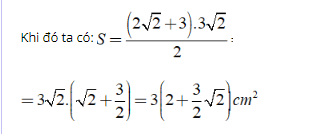
Chọn đáp án B.
Bài 2: Hình thang có độ dài đáy lần lượt là 6cm, 4cm và diện tích hình thang đó là 15cm2. Chiều cao hình thang có độ dài là?
A. 3cm. B. 1,5cm C. 2cm D. 1cm
Diện tích của hình thang là S = 1/2(a + b).h
⇒ (a + b).h = 2S ⇔ h = (2S)/(a + b).
Khi đó, chiều cao của hình thang là h = (2.15)/(6 + 4) = 3cm
Chọn đáp án A.
Bài 3: Cho hình bình hành ABCD (AB//CD) có AB = CD = 4cm, độ dài đường cao hình bình hành là h = 2cm. Diện tích của hình bình hành là?
A. 4cm2 B. 8cm2 C. 6cm2 D. 3cm2
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8cm2
Chọn đáp án B.
Bài 4: Cho hình thang vuông ABCD (Aˆ = Dˆ = 900), trong đó có Cˆ = 450, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3cm2 B. 8cm2 C. 4cm2 D. 6cm2
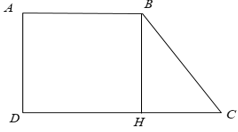
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Mà BCDˆ = 450 ⇒ BDCˆ = 450
⇒ DBCˆ = 1800 - (BCDˆ + BDCˆ) = 1800 - 900 = 900.
⇒ Δ BDC là tam giác vuông cân tại B nên BH = 1/2DC = 2cm.
Do đó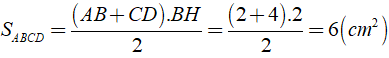
Chọn đáp án D.
II. Bài tập tự luận
Bài 1: Tính diện tích mảnh đất hình thang ABED có AB = 23cm, DE = 31cm và diện tích hình chữ nhật ABCD là 828cm2.
Hướng dẫn:
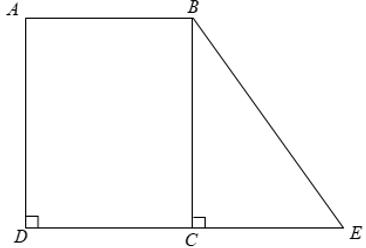
Theo bài ra ta có SABCD = AB.BC = 23.BC = 828 ⇒ BC = 36 ( cm )
Khi đó ta có
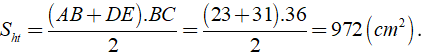
Vậy diện tích hình thang ABED là 972( cm2 )
Bài 2: Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?
Hướng dẫn:
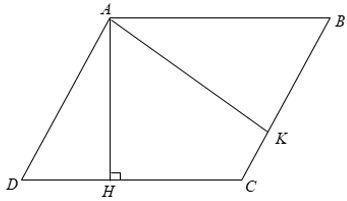
Xét hình bình bình ABCD có AB = CD = 8cm và AD = BC = 6cm
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
+ Shbh = AH.CD = 8.AH
+ Shbh = AK.BC = 6.AK
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5cm thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3cm là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5cm thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4cm là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Diện tích hình thang. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








