Diện tích hình chữ nhật
Chuyên đề Toán học lớp 8: Diện tích hình chữ nhật được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Diện tích hình chữ nhật
A. Lý thuyết diện tích đa giác, diện tích hình chữ nhật
1. Khái niệm diện tích đa giác
Số đo của một phần măt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.
Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.
Diện tích đa giác có các tính chất sau:
+ Hai tam giác bằng nhau thì có diện tích bằng nhau.
+ Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.
2. Công thức diện tích hình chữ nhật
Diện tích hình chữ nhật là tích kích thước 2 cạnh của nó.
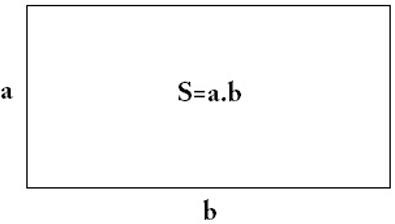
Ta có Shcn = a.b.
Ví dụ: Cho hình chữ nhật có chiều dài bằng 15 cm, chiều rộng bằng 10 cm. Tính diện tích hình chữ nhật đó?
Hướng dẫn:
Diện tích hình chữ nhật cần tìm là Shcn = 15.10 = 150 ( cm2 ).
3. Công thức diện tích hình vuông, diện tích tam giác vuông
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.
Ví dụ: Cho hình vuông có độ dài các cạnh bằng 4 cm. Tính diện tích hình vuông ?
Hướng dẫn:
Diện tích hình vuông cần tìm là Shv = 42 = 16 ( cm2 )
B. Bài tập tính diện tích hình chữ nhật
I. Bài tập trắc nghiệm
Bài 1: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều rộng tăng 4 lần, chiều dài giảm 2 lần?
A. Diện tích không đổi.
B. Diện tích giảm 2 lần.
C. Diện tích tăng 2 lần.
D. Cả đáp án A, B, C đều sai.
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Theo giả thiết: Sban đầu = a.b
Khi đó ta có: Ssau = 4b.1/2a = 2a.b = 2Sban đầu
Do đó, diện tích sau tăng lên 2 lần.
Chọn đáp án C.
Bài 2: Cho hình chữ nhật có chiều dài là 4 cm, chiều rộng là 1,5 cm. Diện tích của hình chữ nhật đó là?
A. 5cm B. 6cm2 C. 6cm D. 5cm2
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Khi đó ta có: Shcn = 4. 1,5 = 6cm2.
Chọn đáp án B.
Bài 3: Cho hình vuông có độ dài cạnh hình vuông là 4 cm. Diện tích của hình vuông đó là?
A. 8cm B. 16cm C. 8cm2 D. 16cm2
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Khi đó ta có Shv = 4.4 = 16 cm2
Chọn đáp án D.
Bài 4: Cho tam giác vuông, có độ dài hai cạnh góc vuông lần lượt là 6cm, 4cm. Diện tích của tam giác vuông đó là?
A. 24cm2 B. 14cm2 C. 12cm2 D. 10cm2
Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.
Khi đó ta có S = 1/2. 6. 4 = 12cm2
Chọn đáp án C.
Bài 5: Cho hình vuông có đường chéo là 6dm thì diện tích là?
A. 12cm2 B. 18cm2 C. 20cm2 D. 24cm2
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Ngoài công thức này, diện tích hình vuông còn một công thức mở rông là:
Diện tích hình vuông bằng nửa tích của hai đường chéo
Khi đó ta có : S = 1/2. 6. 6 = 18cm2
Chọn đáp án B.
II. Bài tập tự luận
Bài 1: Diện tích hình chữ nhật thay đổi như thế nào nếu :
a) Chiều dài tăng hai lần, chiều rộng không đổi
b) Chiều dài và chiều rộng tăng 3 lần.
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần.
Hướng dẫn:
Gọi chiều dài và chiều rộng của một hình chữ nhật lần lượt là a,b
Diện tích hình chữ nhật là Shcn = a.b.
a) Nếu chiều dài tăng lên 2 lần, chiều rộng không đổi thì khi đó chiều dài, chiều rộng mới là là 2a và b
Diện tích hình chữ nhật mới là Sm = 2a.b = 2S.
⇒ Diện tích hình chữ nhật tăng lên 2 lần.
b) Nếu chiều dài và chiều rộng tăng lên 3 lần thì chiều dài, chiều rộng mới là 3a,3b
Diện tích hình chữ nhật mới là Sm = 3a.3b = 9S.
⇒ Diện tích hình chữ nhật tăng lên 9 lần.
c) Nếu chiều dài tăng 4 lần, chiều rộng giảm đi 4 lần thì chiều dài, chiều rộng mới là 4a, 1/4b
Diện tích hình chữ nhật mới là Sm = 4a. 1/4b = ab = S.
⇒ Diện tích hình chữ nhật không đổi.
Bài 2: Tính độ dài các cạnh hình chữ nhật biết rằng
a) Bình phương độ dài một cạnh là 16cm và diện tích hình chữ nhật là 28cm2.
b) Tỉ số các cạnh là 4:9 và diện tích của nó là 144cm2.
Hướng dẫn:
Gọi hai kích thước của hình chữ nhật là a,b (a > 0, b > 0). Khi đó diện tích của hình chữ nhật là Shcn = a.b
a) Theo bài ra ta có: x.y = 28 (1) và x2 = 16 = 42 ⇔ x = 4 (vì x > 0 ), trường hợp y2 = 16 tương tự.
Thay x = 4 vào đẳng thức ( 1 ) ta có: 4y = 28 ⇔ y = 7.
Với x = 4,y = 7 thỏa mãn yêu cầu điều kiện.
Vậy hai kích thức của hình chữ nhật là 4cm, 7cm
b) Theo bài ra ta có x/y = 4/9 (2) và x.y = 144 (3)
Nhân theo vế đẳng thức (2) với (3) ta được x2 = 82 ⇔ x = 8 (vì x > 0)
Thay x = 8 vào đẳng thức (3) ta được 8y = 144 ⇔ y = 18.
Với x = 8,y = 18 thỏa mãn yêu cầu bài toán.
Vậy kích thức của hình chữ nhật là 8cm,18cm.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Diện tích hình chữ nhật. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








