Diện tích hình thoi
Chuyên đề Toán học lớp 8: Diện tích hình thoi được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Diện tích hình thoi
A. Lý thuyết
1. Công thức tính diện tích hình thoi
Diện tích hình thoi bằng nửa tích hai đường chéo.
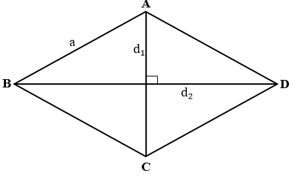
Ta có: S = 1/2d1.d2
Ví dụ: Cho hình thoi có lần lượt độ dài hai đường chéo là 10cm, 15cm. Tính diện tích hình thoi đó?
Hướng dẫn:
Diện tích hình thoi là : S = 1/2.10.15 = 75cm2
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Cho hình thoi có độ dài hai đường chéo lần lượt là 8cm, 10cm. Diện tích hình thoi là?
A. 80cm2. B. 40cm2. C. 18cm2. D. 9cm2.
Diện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2.8.10 = 40( cm2 )
Chọn đáp án B.
Bài 2: Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là?
A. a2√ 6 cm2 B. (a2√ 6 )/3cm2 C. (a2√ 6 )/2cm2 D. (a2√ 5 )/2cm2
Diện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2. a√ 2 . a√ 3 = (a2√ 6 )/2cm2
Chọn đáp án C.
Bài 3: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 600. Diện tích của hình thoi ABCD là?
A. 8cm2 B. 8√ 3 cm2 C. 16cm2 D. 16√ 3 cm2
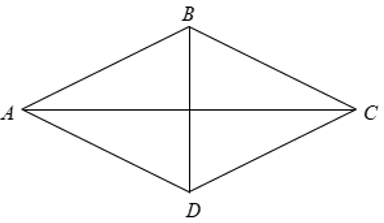
Xét hình thoi ABCD có BACˆ = 600.
Ta có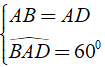
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – ta – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2)
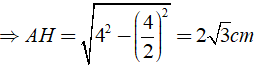
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = 1/2AC.BD = 1/2.4√ 3 .4 = 8√ 3 cm2
Chọn đáp án B.
Bài 4: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là?
A. 16cm2 B. 8√ 21 cm2 C. 16√ 21 cm2 D. 8cm2
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4cm
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10cm
Áp dụng định lý Py – ta – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2) = √ (102 - 42) = 2√ 21 cm
⇒ AC = 2AH = 4√ 21 cm
Do đó SABCD = 1/2.BD.AC = 1/2.4√ (21) .8 = 16√ 21 cm2
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Cho hình thoi ABCD có AB = 13cm, AC = 10cm. Tính diện tích của hình thoi?
Hướng dẫn:
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HA = HC = 5cm
Áp dụng định lí Py – ta – go ta có:
AB2 = AH2 + HB2 ⇒ BH = √ (AB2 - AH2)
⇒ HB = √ (132 - 52) = 12(cm
⇒ BD = HB + HD = 2HB = 2.12 = 24cm
Khi đó ta có SABCD = 1/2AC.BD = 1/2.10.24 = 120 cm2.
Vậy diện tích của hình thoi là 120cm2
Bài 2: Tính diện tích hình thoi có cạnh là 17cm và tổng hai đường chéo là 46cm.
Hướng dẫn:
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46cm
⇔ (HB + HD) + (HC + HA) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23 ⇔ (HA + HB)2 = 232
⇔ HA2 + 2HA.HB + HB2 = 232 (1)
Mặt khác, theo định lí Py – ta – go ta có: AH2 + HB2 = AB2 = 172 (2)
Từ (1) và (2) ta có: 172 + 2HA.HB = 232 ⇒ HA.HB = (232 - 172)/2 = 120.
Hay AC/2.BD/2 = 120 ⇔ 1/2.AC.BD = 240 ⇒ SABCD = 240cm2
Vậy diện tích hình thoi là 240cm2.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Diện tích hình thoi. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
