Bài tập Tính chất đường phân giác của tam giác lớp 8
Chuyên đề Toán học lớp 8: Tính chất đường phân giác của tam giác được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Tính chất đường phân giác của tam giác
A. Lý thuyết
1. Định lý
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
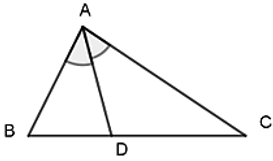
Tổng quát: Δ ABC, AD là đường phân giác của góc 
\(\widehat{BAC}\) (D ∈ BC)
Ta có: \(\frac{DB}{DC}=\frac{AB}{AC}\) hay \(\frac{DB}{AB}=\frac{DC}{AC}\)
Ví dụ: Cho ΔABC có AD là đường phân giác của góc \(\widehat{BAC}\) (D ∈ BC) sao cho DB = 2 cm, có AB = 3 cm, AC = 4 cm. Tính độ dài cạnh DC.
Lời giải:
Áp dụng định lí trên ta có: ΔABC, AD là đường phân giác của góc \(\widehat{BAC}\) (D ∈ BC)
Ta có \(\frac{DB}{AB}=\frac{DC}{AC}\) hay \(\frac{2}{3}=\frac{DC}{4}\)
⇒ \(DC=\frac{8}{3}\) (cm)
2. Chú ý
Định lí vẫn đúng với đường phân giác của góc ngoài của tam giác
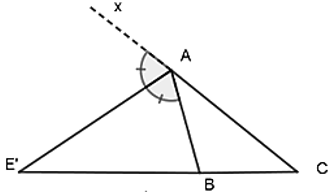
AE' là phân giác của góc \(\widehat{BAx}\) (AB ≠ AC)
Ta có: \(\frac{AB}{AC}=\frac{E'B}{E'C}\text{hay}\ \frac{E'B}{AB}=\frac{E'C}{AC}\)
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Cho ΔABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của ΔABC. Chọn phát biểu đúng?
A. BD = 20/7 cm; CD = 15/7 cm
B. BD = 15/7 cm; CD = 20/7 cm
C. BD = 1,5 cm; CD = 2,5 cm
D. BD = 2,5 cm; CD = 1,5 cm
Lời giải:
Áp dụng định lý Pythagore ta có: \(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\) cm
ΔABC, AD là đường phân giác của góc \(\widehat{BAC}\) (D ∈ BC)
Ta có: \(\frac{DB}{DC}=\frac{AB}{AC}\)
⇒ \(\frac{DB}{5-DB}=\frac{3}{4}\)
⇒ 4DB = 15 - 3DB
⇒ 7DB = 15 ⇒ \(DB=\frac{15}{7}\text{cm};\ DC=\frac{20}{7}\text{cm}\)
Chọn đáp án B.
Bài 2: Cho ΔABC có BD là đường phân giác, AB = 8 cm, BC = 10 cm, AC = 6 cm. Chọn phát biểu đúng?
A. DA = 8/3 cm, DC = 10/3 cm
B. DA = 10/3 cm, DC = 8/3 cm
C. DA = 4 cm, DC = 2 cm
D. DA = 3,5 cm, DC = 2,5 cm
Lời giải:
BD là đường phân giác của ΔABC
Ta có: \(\frac{DA}{DC}=\frac{AB}{BC}\) ⇔ \(\frac{DA}{DA+DC}=\frac{AB}{AB+BC}\)
⇒\(\frac{DA}{6}=\frac{8}{8+10}\) ⇒ \(DA=\frac{8}{3}\) cm
Chọn đáp án A.
Bài 3: Cho ΔABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x?
| A. x = 14 | B. x = 12 | C. x = 8 | D. x = 6 |
Lời giải:
Δ ABC có AD là phân giác trong của góc A.
Ta có: \(\frac{DB}{DC} = \frac{AB}{AC} ⇒ \frac{DB}{BC - DB} = \frac{AB}{AC}\)
Hay \(\frac{9}{21-9} = \frac{6}{x} ⇒ x = 8\)
Chọn đáp án C.
Bài 4: Cho Δ ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác \(\widehat{BAC}\) cắt BC tại D. Tỉ số diện tích của ΔABD và ΔACD là?
| A. 1/4 | B. 1/2 | C. 3/4 | D. 1/3 |
Đường phân giác \(\widehat{BAC}\) cắt BC tại D
Ta có: DB/DC = AB/AC = 15/20 = 3/4
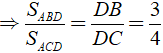
Chọn đáp án C.
II. Bài tập tự luận
Tải file để xem thêm bài tập và đáp án chi tiết!
