Bất phương trình một ẩn
Chuyên đề Toán học lớp 8: Bất phương trình một ẩn được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Bất phương trình một ẩn
A. Lý thuyết
1. Bất phương trình một ẩn
Bất phương trình ẩn x là hệ thức A(x) > B(x) hoặc A(x) < B(x) hoặc A(x) ≥ B(x) hoặc A(x) ≤ B(x).
Trong đó: A(x) gọi là vế trái; B(x) gọi là vế phải.
Nghiệm của bất phương trình là giá trị của ẩn thay vào bất phương trình ta được một khẳng định đúng.
Ví dụ:
Các phương trình một ẩn như: x - 1 < 2x - 3; (x + 1)/2 > - 3; 2(x - 1) ≤ 1 - 3x; 1 - x ≥ 2; ...
2. Tập nghiệm của bất phương trình
Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình đó.
Giải bất phương trình là tìm tập nghiệm của bất phương trình đó.
Ví dụ 1: Tập nghiệm của bất phương trình x > 2 là tập hợp các số lớn hơn 2, tức là tập hợp {x| x > 2}.
Để dễ hình dung, ta biểu diễn tập hợp này trên trục số như hình vẽ sau:
![]()
Ví dụ 2: Tập nghiệm của bất phương trình x ≤ 7 là tập hợp các số nhỏ hơn hoặc bằng 7, tức là tập hợp { x| x ≤ 7 } .
Để dễ hình dung, ta biểu diễn tập hợp này trên trục số như hình vẽ sau:
![]()
3. Bất phương trình tương đương
Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
Kí hiệu là "⇔".
Ví dụ: Bất phương trình x > 3 và bất phương trình 6 < 2x có cùng tập nghiệm là { x| x > 3 }.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Nghiệm x = 3 là nghiệm của bất phương trình nào sau đây?
A. 5 - x < 1
B. 3x + 1 < 4
C. 4x - 11 > x
D. 2x - 1 > 3
Ta có:
+ 5 - x < 1 ⇔ 4 < x
+ 3x + 1 < 4 ⇔ 3x < 2 ⇔ x > 2/3
+ 4x - 11 > x ⇔ 3x > 11 ⇔ x > 11/3
+ 2x - 1 > 3 ⇔ 2x > 4 ⇔ x > 2
Vậy x = 3 là nghiệm của bất phương trình 2x - 1 > 3
Chọn đáp án D.
Bài 2: Tập nghiệm nào sau đây là tập nghiệm của bất phương trình: x ≤ 2 ?
A. S = { x| x ≥ 2 }.
B. S = { x| x ≤ 2 }.
C. S = { x| x ≥ - 2 }.
D. S = { x| x < 2}.
Tập nghiệm của bất phương trình: x ≤ 2 là S = { x| x ≤ 2 }.
Chọn đáp án B.
Bài 3: Hình vẽ sau là tập nghiệm của bất phương trình nào?

A. 2x - 4 < 0
B. 2x - 4 > 0
C. 2x - 4 ≤ 0
D. 2x - 4 ≥ 0
Ta có:
+ 2x - 4 < 0 ⇔ x < 2
+ 2x - 4 > 0 ⇔ x > 2
+ 2x - 4 ≤ 0 ⇔ x ≤ 2
+ 2x - 4 ≥ 0 ⇔ x ≥ 2
Chọn đáp án B.
Bài 4: Cho bất phương trình 3x - 6 > 0. Trong các bất phương trình sau, bất phương trình nào tương đương với bất phương trình đã cho?
A. 2x - 4 < 0
B. 2x - 4 ≥ 0
C. x > 2
D. 1 - 2x < 1
Ta có: 3x - 6 > 0 ⇔ 3x > 6 ⇔ x > 2
Vậy bất phương trình x > 2 tương đương với bất phương trình đã cho.
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Giải bất phương trình sau và biểu diễn nghiệm trên trục số
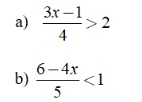
Hướng dẫn:
a) Ta có:![]() ⇔ 3x - 1 > 8
⇔ 3x - 1 > 8
⇔ 3x > 9 ⇔ x > 3
Vậy x > 3 là nghiệm của bất phương trình.
Ta biểu diễn tập nghiệm trên trục số như sau:
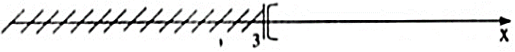
b) Ta có:![]() ⇔ 6 - 4x < 5
⇔ 6 - 4x < 5
⇔ 4x > 1 ⇔ x > 1/4
Vậy x > 1/4 là nghiệm của bất phương trình đã cho.
Ta biểu diễn tập nghiệm trên trục số như sau:
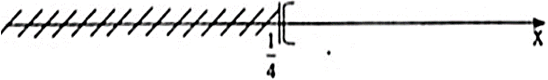
Bài 2: Giải các bất phương trình sau:
a) 3x - 5 < 4
b) 3 - 4x ≥ 19
Hướng dẫn:
a) Ta có: 3x - 5 < 4 ⇔ 3x < 9 ⇔ x < 3
Vậy x < 3 là nghiệm của bất phương trình đã cho.
b) Ta có: 3 - 4x ≥ 19 ⇔ 3 - 19 ≥ 4x ⇔ - 16 ≥ 4x ⇔ x ≤ - 4
Vậy x ≤ - 4 là nghiệm của bất phương trình đã cho.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Bất phương trình một ẩn. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








