Hình thoi
Chuyên đề Toán học lớp 8: Hình thoi được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Hình thoi
A. Lý thuyết
1. Định nghĩa
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Hình thoi cũng là một hình bình hành.
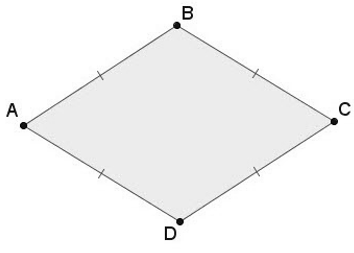
Tổng quát: ABCD là hình thoi \Leftrightarrow AB = BC = CD = DA
2. Tính chất
Hình thoi có tất cả các tính chất của hình bình hành.
Định lí: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác các góc của hình thoi.
3. Dấu hiệu nhận biết hình thoi
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Ví dụ: Cho hình chữ nhật ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD. Chứng minh tứ giác MNPQ là hình thoi.
Hướng dẫn:
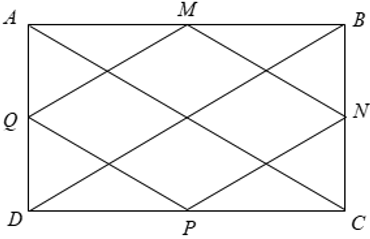
M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD
⇒ AM = MB; BN = NC; CP = DP; AQ = DQ
+ Xét Δ ABD có 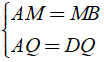
⇒ MQ là đường trung bình của Δ ABD.
⇒ QM = 1/2BD = 1/2AC ( 1 )
+ Xét Δ ABC có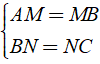
⇒ MN là đường trung bình của Δ ABC.
⇒ MN = 1/2BD = 1/2AC ( 2 )
+ Xét Δ BCD có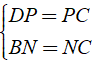
⇒ NP là đường trung bình của Δ BCD.
⇒ NP = 1/2BD = 1/2AC ( 3 )
+ Xét Δ ADC có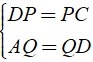
⇒ QP là đường trung bình của Δ ADC.
⇒ QP = 1/2BD = 1/2AC ( 4 )
Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.
⇒ MNPQ là hình thoi.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Khoanh tròn vào phương án đúng trong các phương án sau ?
A. Hình thoi là tứ giác có bốn góc bằng nhau.
B. Hình thoi là tứ giác có hai cạnh đối bằng nhau.
C. Hình thoi là tứ giác có ba góc vuông.
D. Hình thoi là tứ giác có bốn cạnh bằng nhau.
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Chọn đáp án D.
Bài 2: Trong các khẳng định sau, khẳng định nào sai về hình thoi?
A. Hai đường chéo bằng nhau.
B. Hai đường chéo vông góc và là các đường phân giác của các góc hình thoi.
C. Hai đường chéo cắt nhau tại trung điểm mỗi đường.
D. Hình thoi có 4 cạnh bằng nhau.
Định lí: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác các góc của hình thoi.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ Đáp án A sai.
Chọn đáp án A.
Bài 3: Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Độ dài cạnh của hình thoi đó là ?
A. 6cm. B. √ 41 cm. C. √ 164 cm. D. 9cm.
Độ dài đường chéo của hình thoi lần lượt là
→ Độ dài đường chéo của hình thoi là:
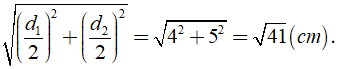
Chọn đáp án B.
Bài 4: Hình thoi có độ dài các cạnh là thì chu vi của hình thoi là?
A. 8cm. B. 44cm. C. 16cm. D. Cả A, B, C đều sai.
Chu vi của hình thoi là Pht = 4 + 4 + 4 + 4 = 16cm.
Chọn đáp án C.
Bài 5: Các phương án sau, phương án nào sai?
A. Các trung điểm của bốn cạnh hình chữ nhật là các đỉnh của một hình thoi.
B. Các trung điểm của bốn cạnh hình thoi là bốn đỉnh của hình chữ nhật.
C. Giao điểm của hai đường chéo của hình thoi là tâm đối xứng của hình thoi đó.
D. Hình thoi của bốn trục đối xứng.
Định lí:
+ Hai thoi có hai trực đối xứng là hai đường chéo của hình thoi.
+ Có một tâm đối xứng là giao điểm của hai đường chéo.
Mở rộng:
+ Trong hình chữ nhật, các trung điểm của các cạnh hĩnh chữ nhật là các đỉnh của một hình thoi.
+ Trong hình thoi, các trung điểm của bốn cạnh hình thoi là các hình chữ nhật.
→ Đáp án D sai.
Chọn đáp án D.
II. Bài tập tự luận
Bài 1: Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đội cạnh đó. Tính các góc của hình thoi.
Hướng dẫn:
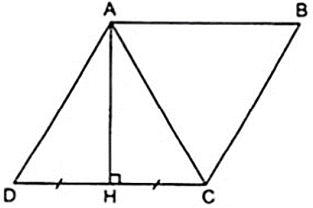
Gọi H là chân đường cao kẻ từ đỉnh A xuống cạnh CD, theo giả thiết ta có:
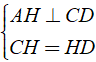 ⇒ AH là đường trung trực của đoạn CD nên AC = AD (1)
⇒ AH là đường trung trực của đoạn CD nên AC = AD (1)
Áp dụng định nghĩa của hình thoi ABCD, ta có
AD = AB = BC = CD (2)
Từ (1) và (2) ta có AD = AC = CD ⇒ Δ ACD là tam giác đều
⇒ ADCˆ = 600.
Vì góc A và góc D là hai góc trong cùng phía của AB//CD nên chúng bù nha.
Hay Aˆ + Dˆ = 1800 ⇒ Aˆ = 1800 - Dˆ = 1800 - 600 = 1200.
Áp dụng tính chất về góc của hình thoi ta có: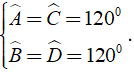
Bài 2: Chứng minh rằng các đường cao của hình thoi bằng nhau.
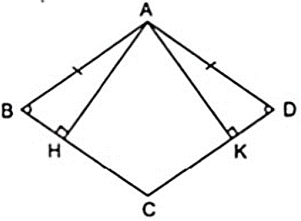
Hướng dẫn:
Xét hình thoi ABCD, kẻ hai đường cao
AH ⊥ BC, AK ⊥ CD.
Ta cần chứng minh: AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:
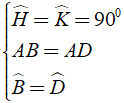 ⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ AH = AK (cặp cạnh tương ứng bằng nhau)
→ (đpcm)
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Hình thoi. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








