Giải Toán 8 bài 11: Hình thoi

Giải SGK Toán 8 bài 11: Hình thoi với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.

Trả lời câu hỏi Toán 8 Tập 1 Bài 11 trang 104

Chứng minh rằng tứ giác ABCD trên hình 100 cũng là một hình bình hành.

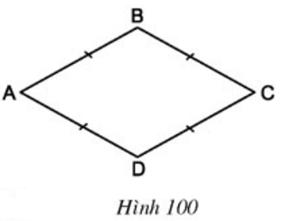
Lời giải

ABCD có các cặp cạnh đối bằng nhau ⇒ ABCD là hình bình hành

Trả lời câu hỏi Toán 8 Tập 1 Bài 11 trang 104:

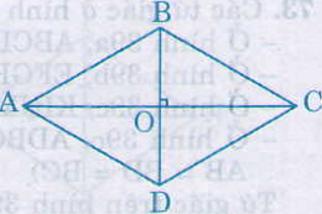
Cho hình thoi ABCD, hai đường chéo cắt nhau tại O (h.101).

a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất gì?

b) Hãy phát hiện thêm các tính chất khác của hai đường chéo AC và BD.

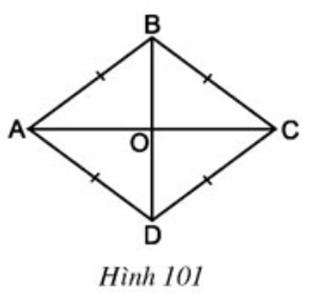
Lời giải

a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất cắt nhau tại trung điểm mỗi đường

b) Xét ΔAOB và ΔCOB

AB = CB

BO chung

OA = OC (O là trung điểm AC)

⇒ ΔAOB = ΔCOB (c.c.c)

⇒ (AOB) = (COB) ,(ABO) = (CBO) (các cặp góc tương ứng)

(ABO) = (CBO) ⇒ BO là phân giác góc ABC

(AOB) + (COB) = 180^o ⇒(AOB) = (COB) = 180^o : 2 = 90^o

Chứng minh tương tự, ta kết luận được:

AC, BD là các đường phân giác của các góc của hình thang

và AC ⊥ BD tại O

Trả lời câu hỏi Toán 8 Tập 1 Bài 11 trang 105:

Hãy chứng minh dấu hiệu nhận biết 3.

Lời giải

Dấu hiệu nhận biết 3: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi

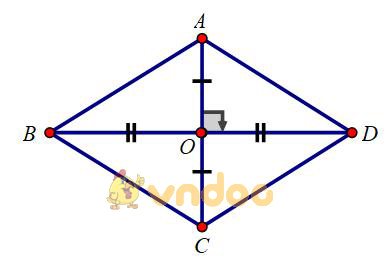
ABCD là hình bình hành ⇒ O là trung điểm AC và O là trung điểm BD

Xét hai tam giác vuông AOB và AOD có:

OA chung

OB = OD (O là trung điểm BD)

⇒ ΔAOB = ΔAOD (hai cạnh góc vuông)

⇒ AB = AD (hai cạnh tương ứng)

Hình bình hành ABCD ⇒ AB = CD và AD = BC

Do đó AB = BC = CD = DA ⇒ ABCD là hình thoi

Bài 73 (trang 105 SGK Toán 8 Tập 1):

Tìm các hình thoi trên hình 102.

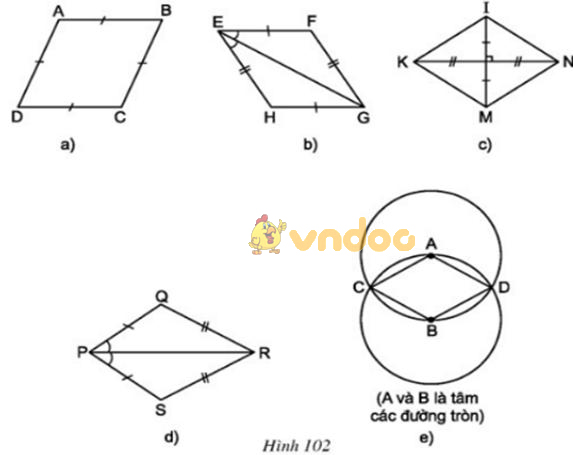
Lời giải:

Các tứ giác ở hình 102a, b, c, e là hình thoi.

– Hình 102a: ABCD là hình thoi (theo định nghĩa)

– Hình 102b: EFGH là hình thoi (theo dấu hiệu nhận biết 4)

- Hình 102c: KINM là hình thoi (theo dấu hiệu nhận biết 3)

– Hình 102e: ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)

Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.

Bài 74 (trang 106 SGK Toán 8 Tập 1):

Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

A. 6cm;

B. √41 cm ;

c) √164cm ;

d) 9cm

Lời giải:

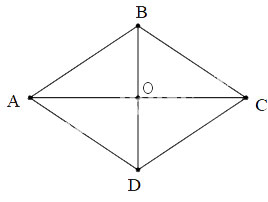
Xét bài toán:

ABCD là hình thoi, O là giao điểm hai đường chéo AC = 10cm; BD = 8cm

Theo tính chất của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.

\(\Rightarrow \left\{ \begin{array}{l} OA = \dfrac{{AC}}{2}=5cm\\ OB = \dfrac{{B{\rm{D}}}}{2}=4cm \end{array} \right.\)

Áp dụng định lí Pytago vào tam giác vuông ABO ta có:

\(\eqalign{ & A{B^2} = O{A^2} + O{B^2} \cr&\;\;\;\;\;\;\;\;= 5^2 + 4^2 \cr & \Rightarrow AB= \sqrt { {5^2}+{4^2} } = \sqrt {41} cm \cr}\)

Vậy (B) đúng.

Bài 75 (trang 106 SGK Toán 8 Tập 1):

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.

Lời giải:

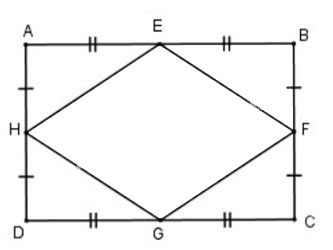
Giả sử hình chữ nhật ABCD có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA

Bốn tam giác vuông EAH, EBF, GDH, GCF có:

\(AE = BE = DG = CG ( = \dfrac{1}{2}AB = \dfrac{1}{2}CD )\)

\(HA = FB = DH = CF ( = \dfrac{1}{2}AD = \dfrac{1}{2}BC )\)

Xét ∆EAH và ∆EBF có:

\(\left\{ \begin{array}{l} A{\rm{E}} = BE\left( {cmt} \right)\\ \widehat A = \widehat B = {90^0}\left( {gt} \right)\\ AH = BF\left( {cmt} \right) \end{array} \right.\)

\(\Rightarrow \Delta AHE = \Delta BEF\left( {c - g - c} \right)\)

\(\Rightarrow EH = EF\) (2 cạnh tương ứng) (1)

Xét ∆HDG và ∆FCG có:

\(\left\{ \begin{array}{l} H{\rm{D}} = FC\left( {cmt} \right)\\ \widehat D = \widehat C = {90^0}\left( {gt} \right)\\ DG = CG\left( {cmt} \right) \end{array} \right.\)

\(\Rightarrow \Delta HDG = \Delta FCG\left( {c - g - c} \right)\)

\(\Rightarrow GH = GF\) (2 cạnh tương ứng) (2)

Xét ∆AHE và ∆DHG có:

\(\left\{ \begin{array}{l} H{\rm{A}} = HD\left( {cmt} \right)\\ \widehat A = \widehat D = {90^0}\left( {gt} \right)\\ AE = DG\left( {cmt} \right) \end{array} \right.\)

\(\Rightarrow \Delta AHE = \Delta DHG\left( {c - g - c} \right)\)

\(\Rightarrow EH = HG\) (2 cạnh tương ứng) (3)

Từ (1), (2) và (3) \(\Rightarrow HE=EF = HG = GF\)

⇒ EFGH là hình thoi (dấu hiệu nhận biết hình thoi).

Bài 76 (trang 105 SGK Toán 8 Tập 1):

Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

Lời giải:

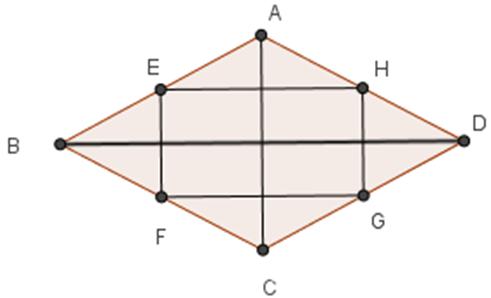
Ta có: EB = EA, FB = FA (gt)

Nên EF là đường trung bình của ΔABC.

Do đó EF // AC

HD = HA, GD = GC (gt) nên HG là đường trung bình của ΔADC.

Do đó HG // AC

Suy ra EF // HG (1)

Chứng minh tương tự EH // FG (2)

Từ (1) và (2) ta được EFGH là hình bình hành

Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH

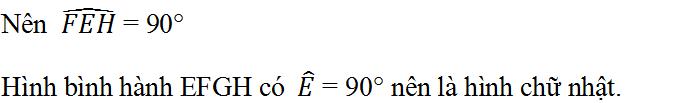
Bài 77 (trang 106 SGK Toán 8 Tập 1):

Chứng minh rằng:

a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

Lời giải:

a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.

Hình thoi cũng là một hình bình hành nên giao điểm của hai đường chéo hình thoi là tâm đối xứng của hình.

b)

- BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.

- Mọi điểm trên BD đều đối xứng qua chính đường thẳng BD. (*)

- Tâm O là tâm đối xứng mà O ∈ BD

=> BD là trục đối xứng của hình thoi. (**)

- Tương tự AC cũng là là trục đối xứng của hình thoi.

((*) Điểm đối xứng của điểm B qua BD chính là điểm B.

(**) Định nghĩa trục đối xứng: Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.)

Bài 78 (trang 106 SGK Toán 8 Tập 1):

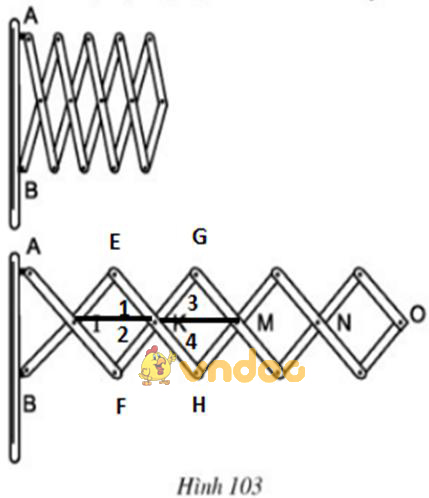
Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng?

Lời giải:

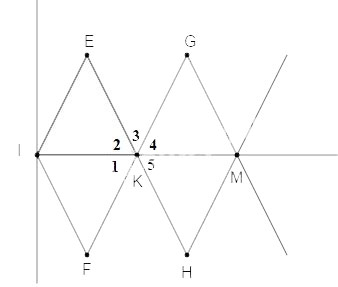
Các tứ giác IEKF, KGMH là hình thoi (gt)

⇒ KI là phân giác của \(\widehat {EKF}\), KM là phân giác của \(\widehat{HKG}\) (tính chất hình thoi)

Mà \(\widehat{EKF} = \widehat{HKG}\) (đối đỉnh)

\(\Rightarrow \widehat{K_{1}} = \widehat{K_{2}} = \widehat{K_{4}} = \widehat{K_{5}}\)

Do đó \(\widehat{K_{2}} +\widehat{K_{3}} + \widehat{K_{4}} = \widehat{K_{2}} + \widehat{K_{3}} + \widehat{K_{1}}\,={180^o}\)

Suy ra I, K, M thẳng hàng.

Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.

............................................

Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải SGK Toán 8 bài 11: Hình thoi. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.

Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải bài tập Toán lớp 8, Giải vở bài tập Toán 8, soạn bài 8 hoặc đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với Tài liệu học tập lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt.

Bài tiếp theo: Giải Toán 8 bài 12: Hình vuông

Xem thêm

• Giải bài tập SGK Toán lớp 8 bài 8: Đối xứng tâm
• Giải bài tập SGK Toán lớp 8 bài 9: Hình chữ nhật
• Giải bài tập SGK Toán lớp 8 bài 10: Đường thẳng song song với một đường thẳng cho trước