Giải Toán 8 bài 4: Quy đồng mẫu thức nhiều phân thức

Giải bài tập SGK Toán lớp 8 bài 4: Quy đồng mẫu thức nhiều phân thức với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm đáp án cho các câu hỏi trong SGK Toán 8, giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.

Trả lời câu hỏi Toán 8 Tập 1 Bài 4 trang 41, 42, 43

Trả lời câu hỏi Toán 8 Tập 1 Bài 4 trang 41

Cho hai phân thức

.

Có thể chọn mẫu thức chung là 12x² y³z hoặc 24x³ y⁴z hay không? Nếu được thì mẫu thức chung nào đơn giản hơn?

Lời giải

Có thể chọn mẫu thức chung là 12x²y³ z hoặc 24x³y⁴z

Chọn mẫu thức chung là 12x²y³z đơn giản hơn

Trả lời câu hỏi Toán 8 Tập 1 Bài 4 trang 42:

Quy đồng mẫu thức hai phân thức:

Lời giải

x² - 5x = x(x - 5)

2x - 10 = 2(x - 5)

=> Mẫu thức chung là: 2x(x-5)

Vì 2x(x - 5) = 2. x(x - 5) = 2 . (x² - 5x) nên phải nhân cả tử và mẫu của phân thức thứ nhất với 2:

Vì 2x(x-5) = x. 2(x-5) = x. (2x – 10) nên phải nhân cả tử và mẫu của phân thức thứ hai với x:

Trả lời câu hỏi Toán 8 Tập 1 Bài 4 trang 43:

Quy đồng mẫu thức hai phân thức:

Lời giải

Ta có:

x² - 5x = x(x - 5)

2x - 10 = 2(x - 5)

⇒ Mẫu thức chung là: 2x(x - 5)

Vì 2x(x - 5) = 2. x(x - 5) = 2 . (x² - 5x) nên phải nhân cả tử và mẫu của phân thức thứ nhất với 2:

Vì 2x(x-5) = x. 2(x-5) = x. (2x – 10) nên phải nhân cả tử và mẫu của phân thức thứ hai với x:

Giải Toán 8 tập 1 trang 43

Bài 14 (trang 43 SGK Toán 8 Tập 1):

Quy đồng mẫu thức các phân thức sau:

Lời giải:

a) Mẫu thức chung: \(12{x^5}{y^4}\)

Nhân tử phụ:

\(12{x^5}{y^4}:{\rm{ }}{x^5}{y^3} = {\rm{ }}12y\)

\(12{\rm{ }}{x^5}{y^4}:{\rm{ }}12{x^3}{y^4} = {\rm{ }}x^2\)

Quy đồng:

\(\dfrac{5}{x^{5}y^{3}}= \dfrac{5.12y}{x^{5}y^{3}.12y}= \dfrac{60y}{12x^{5}y^{4}}\)

\(\dfrac{7}{12x^{3}y^{4}}= \dfrac{7x^{2}}{12x^{3}y^{4}.x^{2}}= \dfrac{7x^{2}}{12x^{5}y^{4}}\)

b) Mẫu thức chung: \(60{x^4}{y^5}\)

Nhân tử phụ: \(60{x^4}{y^5}:{\rm{ }}15{x^3}{y^5} = {\rm{ }}4x\)

\(60{x^4}{y^5}:{\rm{ }}12{x^4}{y^2} = {\rm{ }}5{y^3}\)

Quy đồng:

\(\dfrac{4}{15x^{3}y^{5}}= \dfrac{4.4x}{15x^{3}y^{{5}}.4x}= \dfrac{16x}{60x^{4}y^{5}}\)

\(\dfrac{11}{12x^{4}y^{2}}= \dfrac{11.5y^{3}}{12x^{4}y^{2}.5y^{3}}= \dfrac{55y^{3}}{60x^{4}y^{5}}\)

Bài 15 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu các phân thức sau:

Lời giải:

a) Tìm mẫu thức chung:

\(2x + 6 = 2(x + 3)\)

\(x^2- 9 = (x -3)(x + 3)\)

Mẫu thức chung là: \(2(x - 3)(x + 3)\)

Nhân tử phụ thứ nhất là: (x-3)

Nhân tử phụ thứ hai là: 2

Quy đồng:

\(\dfrac{5}{2x +6}=\dfrac{5}{2(x+3)}=\dfrac{5(x-3)}{2(x-3)(x+3)}\)

\(\dfrac{3}{x^{2}-9}= \dfrac{3}{(x-3)(x+3)}= \dfrac{3.2}{2(x-3)(x+3)}=\dfrac{6}{2(x-3)(x+3)}\)

b) Tìm mẫu thức chung:

\({x^2}-{\rm{ }}8x{\rm{ }} + {\rm{ }}16{\rm{ }} = {x^2} - 2.x.4 + {4^2}= {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}4} \right)^2}\)

\(3x^2– 12x = 3x(x - 4)\)

Mẫu thức chung là: \(3x(x - 4)^2\)

Nhân tử phụ thứ nhất là: 3x

Nhân tử phụ thứ hai là: (x-4)

Quy đồng:

\(\dfrac{2x}{x^{2}-8x+16}=\dfrac{2x}{(x-4)^{2}}=\dfrac{2x.3x}{3x(x-4)^{2}}=\dfrac{6x^{2}}{3x(x-4)^{2}}\)

\(\dfrac{x}{3x^{2}-12}=\dfrac{x}{3x(x-4)}=\dfrac{x(x-4)}{3x(x-4)^{2}}\)

Bài 16 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):

Lời giải:

a) Tìm mẫu thức chung:

\({x^3} - 1 = \left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Nên mẫu thức chung là: \(\left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Nhân tử phụ thứ nhất là 1

Nhân tử phụ thứ hai là (x-1)

Nhân tử phụ thứ ba là \(\left( {x - 1} \right)({x^2} + {\rm{ }}x + 1)\)

Quy đồng:

\(\dfrac{4x^{2}-3x+5}{x^{3}-1}=\dfrac{4x^{2}-3x+5}{(x-1)(x^{2}+x+1)}\)

\(\dfrac{1-2x}{x^{2}+x+1}=\dfrac{(x-1)(1-2x)}{(x-1)(x^{2}+x+1)}\)

\(-2 = \dfrac{-2(x^{3}-1)}{(x-1)(x^{2}+x+1)}\)

b) Tìm mẫu thức chung:

\(x+ 2=x+2\)

\(2x - 4 = 2(x - 2)\)

\(6 - 3x = 3(2 - x) = -3(x -2)\)

Mẫu thức chung là: 6(x - 2)(x + 2)

Nhân tử phụ thứ nhất là 6(x-2)

Nhân tử phụ thứ hai là 3(x+2)

Nhân tử phụ thứ ba là -2(x+2)

Quy đồng:

\(\dfrac{10}{x+2}= \dfrac{10.6.(x-2)}{6(x-2)(x+2)}=\dfrac{60(x-2)}{6(x-2)(x+2)}\)

\(\dfrac{5}{2x-4}=\dfrac{5}{2(x-2)}=\dfrac{5.3(x+2)}{2(x-2).3(x+2)}=\dfrac{15(x+2)}{6(x-2)(x+2)}\)

\(\dfrac{1}{6-3x}=\dfrac{1}{-3(x-2)}=\dfrac{-2(x+2)}{-3(x-2).[-2(x+2)]}=\dfrac{-2(x+2)}{6(x-2)(x+2)}\)

Bài 17 (trang 43 SGK Toán 8 Tập 1)

Đố. Cho hai phân thức: \(\dfrac{5x^{2}}{x^{3}-6x^{2}},\dfrac{3x^{2}+18x}{x^{2}-36}\)

Khi quy đồng mẫu thức, bạn Tuấn đã chọn \(MTC = {x^2}\left( {x - 6} \right)\left( {x + 6} \right)\) còn bạn Lan bảo rằng: "Quá đơn giản! MTC = x - 6". Đố em biết bạn nào chọn đúng?

Lời giải:

Cách làm của bạn Tuấn:

Bạn Tuấn trực tiếp đi tìm mẫu thức chung theo quy tắc:

\(\begin{array}{l} {x^3} - 6{{\rm{x}}^2} = {x^2}\left( {x - 6} \right)\\ {x^2} - 36 =x^2-6^2= \left( {x - 6} \right)\left( {x + 6} \right)\\ MTC = {x^2}\left( {x - 6} \right)\left( {x + 6} \right) \end{array}\)

Do đó bạn Tuấn làm đúng.

Cách làm của bạn Lan:

Bạn Lan rút gọn phân thức trước khi đi tìm mẫu thức chung:

\(\begin{array}{l} \dfrac{{5{{\rm{x}}^2}}}{{{x^3} - 6{{\rm{x}}^2}}} = \dfrac{{5{{\rm{x}}^2}}}{{{x^2}\left( {x - 6} \right)}} = \dfrac{5}{{x - 6}}\\ \dfrac{{3{{\rm{x}}^2} + 18{\rm{x}}}}{{{x^2} - 36}} = \dfrac{{3{\rm{x}}\left( {x + 6} \right)}}{{\left( {x - 6} \right)\left( {x + 6} \right)}} = \dfrac{{3{\rm{x}}}}{{x - 6}} \end{array}\)

Do đó MTC = x - 6. Vậy bạn Lan làm đúng.

Vậy cả hai bạn đều làm đúng. Bạn Tuấn đã tìm MTC theo đúng qui tắc. Bạn Lan thì rút gọn các phân thức trước khi tìm MTC.

Nhận xét: Ta nên rút gọn hoàn toàn các phân thức trước khi quy đồng để việc quy đồng ngắn gọn hơn.

Giải bài tập Toán 8 trang 43, 44 tập 1: Luyện tập

Bài 18 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức hai phân thức:

a) \(\dfrac{{3x}}{{2x + 4}}\) và \(\dfrac{{x + 3}}{{{x^2} - 4}}\)

b) \(\dfrac{{x + 5}}{{{x^2} + 4x + 4}}\) và \(\dfrac{x}{{3x + 6}}\)

Lời giải:

a) + Phân tích mẫu thức thành nhân tử để tìm mẫu thức chung

2x + 4 =2(x+2)

\({x^2} - 4 = \left( {x - 2} \right)\left( {x + 2} \right)\)

\(⇒ MTC = 2\left( {x - 2} \right)\left( {x + 2} \right) = 2\left( {{x^2} - 4} \right)\)

+ Nhân tử phụ:

\(2\left( {x - 2} \right)\left( {x + 2} \right) :2(x+2)=x-2\)

\(2\left( {x - 2} \right)\left( {x + 2} \right) :(x-2)(x+2)=2\)

+ Quy đồng:

\(\dfrac{{3x}}{{2x + 4}} = \dfrac{{3x\left( {x - 2} \right)}}{{2\left( {x + 2} \right)\left( {x - 2} \right)}} = \dfrac{{3x\left( {x - 2} \right)}}{{2\left( {{x^2} - 4} \right)}}\)

\(\dfrac{{x + 3}}{{{x^2} - 4}} = \dfrac{{\left( {x + 3} \right).2}}{{\left( {x - 2} \right)\left( {x + 2} \right).2}} = \dfrac{{2\left( {x + 3} \right)}}{{2\left( {{x^2} - 4} \right)}}\)

b) + Phân tích mẫu thức thành nhân tử để tìm mẫu thức chung

\({x^2} + 4x + 4 = {x^2} + 2.x.2 + {2^2}= {\left( {x + 2} \right)^2}\)

\(3x + 6 = 3\left( {x + 2} \right)\)

Nên \(MTC = 3{\left( {x + 2} \right)^2}\)

+ Nhân tử phụ:

\(3{\left( {x + 2} \right)^2}:(x+2)^2=3\)

\(3{\left( {x + 2} \right)^2}:3(x+2)=x+2\)

+ Quy đồng:

\(\dfrac{{x + 5}}{{{x^2} + 4x + 4}} = \dfrac{{\left( {x + 5} \right).3}}{{{{\left( {x + 2} \right)}^2}.3}} = \dfrac{{3\left( {x + 5} \right)}}{{3{{\left( {x + 2} \right)}^2}}}\)

\(\dfrac{x}{{3x + 6}} = \dfrac{{x.\left( {x + 2} \right)}}{{3\left( {x + 2} \right).\left( {x + 2} \right)}} = \dfrac{{x\left( {x + 2} \right)}}{{3{{\left( {x + 2} \right)}^2}}}\)

Bài 19 (trang 43 SGK Toán 8 Tập 1)

Quy đồng mẫu thức các phân thức sau:

Lời giải:

a) + Phân tích mẫu thức thành nhân tử để tìm MTC

2x – x^2 = x.(2 – x)

\(MTC = x\left( {2 - x} \right)\left( {2 + x} \right)\)

+ Nhân tử phụ :

\(x.(2-x)(x+2) : (x + 2) = x.(2 – x)\)

\(x(2-x)(x+2) : x(2 – x) = x + 2\)

+ Quy đồng:

\(\dfrac{1}{{x + 2}} = \dfrac{1}{{2 + x}} = \dfrac{{x\left( {2 - x} \right)}}{{x\left( {2 - x} \right)\left( {2 + x} \right)}} = \dfrac{{2x - {x^2}}}{{x(2 - x)(2 + x)}}\)

\(\dfrac{8}{{2x - {x^2}}} = \dfrac{{8.(2 + x)}}{{x(2 - x)(2 + x)}} = \dfrac{{16 + 8x}}{{x(2 - x)(2 + x)}}\)

b) \(MTC = {x^2} - 1\)

Quy đồng:

\({x^2} + 1 = \dfrac{{{x^2} + 1}}{1} = \dfrac{{\left( {{x^2} + 1} \right)\left( {{x^2} - 1} \right)}}{{{x^2} - 1}} = \dfrac{{{x^4} - 1}}{{{x^2} - 1}}\)

\(\dfrac{{{x^4}}}{{{x^2} - 1}}\) giữ nguyên.

c) Ta có: \(\dfrac{x}{{{y^2} - xy}} = \dfrac{-x}{{xy-y^2}}\)

+ Phân tích mẫu thức thành nhân tử:

\({x^3} - 3{x^2}y + 3x{y^2} - {y^3} = {\left( {x - y} \right)^3}\)

\(xy-{y^2} = y\left( {x - y} \right)\)

\(MTC = y{\left( {x - y} \right)^3}\)

+ Nhân tử phụ:

\(y(x – y)^3 : (x – y)^3 = y\)

\(y(x – y)^3 : y(x – y) = (x – y)^2\)

+ Quy đồng mẫu thức:

\(\dfrac{{{x^3}}}{{{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}} = \dfrac{{{x^3}}}{{{{\left( {x - y} \right)}^3}}} = \dfrac{{{x^3}y}}{{y{{\left( {x - y} \right)}^3}}}\)

\(\dfrac{x}{{{y^2} - xy}} = \dfrac{-x}{{xy-y^2}} = \dfrac{{ - x}}{{y\left( {x - y} \right)}} = \dfrac{{ - x{{\left( {x - y} \right)}^2}}}{{y(x-y).{{(x - y)}^2}}}= \dfrac{{ - x{{\left( {x - y} \right)}^2}}}{{y{{(x - y)}^3}}}\)

Bài 20 (trang 44 SGK Toán 8 Tập 1)

Cho hai phân thức:

\(\dfrac{1}{{{x^2} + 3x - 10}},\;\dfrac{x}{{{x^2} + 7x + 10}}\)

Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là: \({x^3} + 5{x^2} - 4x - 20\).

Lời giải:

Để chứng tỏ rằng có thể chọn đa thức \({x^3} + 5{x^2} - 4x - 20\) làm mẫu thức chung ta chỉ cần chứng tỏ rằng nó chia hết cho mẫu thức của mỗi phân thức đã cho.

Ta xét các phép chia:

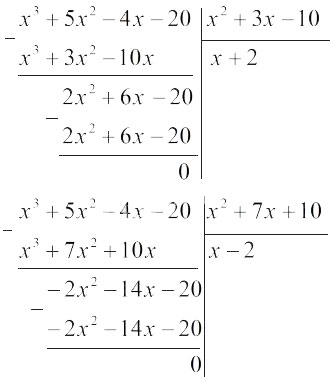
Do đó:

\(\begin{array}{l} {x^3} + 5{{\rm{x}}^2} - 4{\rm{x}} - 20\\ = \left( {{x^2} + 3{\rm{x}} - 10} \right)\left( {x + 2} \right)\\ = \left( {{x^2} + 7{\rm{x + }}10} \right)\left( {x - 2} \right) \end{array}\)

+) \(MTC = {x^3} + 5{x^2} - 4x - 20\)

Nhân tử phụ của mẫu thứ nhất là: (x+2)

Nhân tử phụ của mẫu thứ hai là: (x-2)

+) Quy đồng mẫu thức:

\(\dfrac{1}{{{x^2} + 3x - 10}} = \dfrac{{1.\left( {x + 2} \right)}}{{\left( {{x^2} + 3x - 10} \right)\left( {x + 2} \right)}}= \dfrac{{x + 2}}{{{x^3} + 5{x^2} - 4x - 20}}\)

\(\dfrac{x}{{{x^2} + 7x + 10}}= \dfrac{{x\left( {x - 2} \right)}}{{\left( {{x^2} + 7x + 10} \right)\left( {x - 2} \right)}}= \dfrac{{{x^2} - 2x}}{{{x^3} + 5{x^2} - 4x - 20}}\)

............................

Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải Toán 8 bài 4: Quy đồng mẫu thức nhiều phân thức. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.

Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải SBT Toán 8, Giải Vở BT Toán 8 và các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa... được cập nhật liên tục trên VnDoc.

Mời các bạn tham khảo thêm tài liệu liên quan

• Giải bài tập trang 22, 23 SGK Toán lớp 8 tập 1: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
• Giải bài tập trang 24, 25 SGK Toán lớp 8: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
• Giải bài tập SGK trang 26, 27 Toán 8 tập 1: Chia đơn thức cho đơn thức