Giải Toán 8 bài 1 Tứ giác

Giải SGK Toán 8 trang 64, 65, 66, 67

Toán 8 bài 1: Tứ giác

A. Lý thuyết Tứ giác
B. Trả lời câu hỏi trang 64, 65 SGK Toán 8 tập 1
C. Giải bài tập trang 66, 67 Toán 8 tập 1

Giải Toán 8 bài 1 Tứ giác tổng hợp câu hỏi và đáp án cho từng bài tập trong SGK Toán lớp 8 trang 64, 65, 66 tập 1. Lời giải Toán 8 được trình bày chi tiết rõ ràng, giúp các em nắm vững kiến thức cơ bản về tứ giác, từ đó luyện giải Toán 8 hiệu quả và học tốt Toán 8 hơn. Sau đây mời các bạn tham khảo chi tiết.

A. Lý thuyết Tứ giác

Định nghĩa: Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

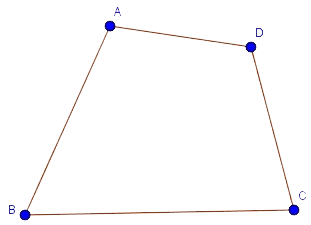
Tứ giác lồi

Định nghĩa: Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.

Ví dụ: Tứ giác ABCD trên gọi là tứ giác lồi.

B. Trả lời câu hỏi trang 64, 65 SGK Toán 8 tập 1

Câu hỏi 1 trang 64 SGK Toán 8 tập 1

Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác?

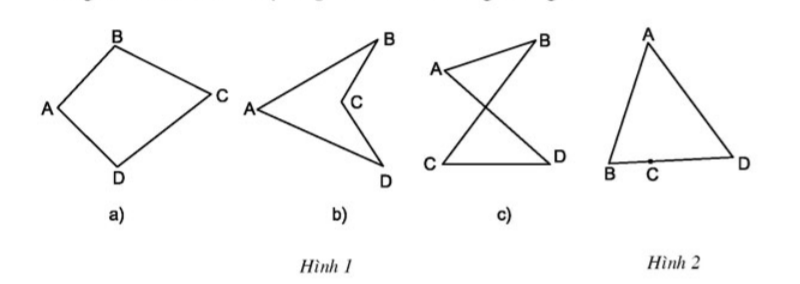
Câu hỏi 1 trang 64 SGK Toán 8 tập 1

Hướng dẫn giải:

a. Tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

b. Tứ giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

c. Tứ giác nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC)

Câu hỏi 2 trang 65 SGK Toán 8 tập 1

Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:

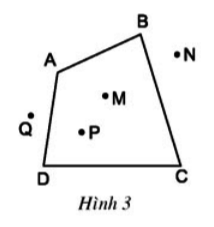
Câu hỏi 2 trang 65 SGK Toán 8 tập 1

a) Hai đỉnh kề nhau: A và B, …

Hai đỉnh đối nhau: A và C, …

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …

c) Hai cạnh kề nhau: AB và BC, …

Hai cạnh đối nhau: AB và CD, …

d) Góc: ∠A , …

Hai góc đối nhau: ∠A và ∠C , …

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …

Hướng dẫn giải:

a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A

Hai đỉnh đối nhau: A và C, B và D

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD

c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB

Hai cạnh đối nhau: AB và CD, AD và BC

d) Góc: ∠A , ∠B , ∠C , ∠D

Hai góc đối nhau: ∠A và ∠C , ∠B và ∠D

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q

Câu hỏi 3 trang 65 SGK Toán 8 tập 1

a) Nhắc lại định lý về tổng ba góc của một tam giác

b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng $\widehat A + \widehat B + \widehat C + \widehat D$ $\widehat A + \widehat B + \widehat C + \widehat D$

Hướng dẫn giải:

a) Trong một tam giác, tổng ba góc là 180^o

b)

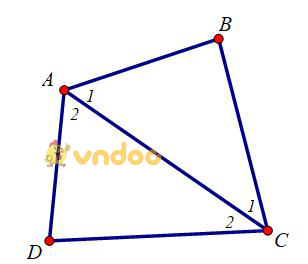
Giải bài tập SGK Toán lớp 8 bài 1: Tứ giác

ΔABC có ∠A₁ + ∠B + ∠C₁ = 180^o

ΔADC có ∠A₂ + ∠D + ∠C₂ = 180^o

⇒ ∠A₁ + ∠B + ∠C₁ + ∠A₂ + ∠D + ∠C₂ = 180^o + 180^o

⇒ (∠A₁ + ∠A₂ ) + ∠B + (∠C₁ + ∠C₂) + ∠D = 360^o

⇒ ∠A + ∠B + ∠C + ∠D = 360^o

C. Giải bài tập trang 66, 67 Toán 8 tập 1

Bài 1 (trang 66 SGK Toán 8 Tập 1):

Tìm x ở hình 5, hình 6:

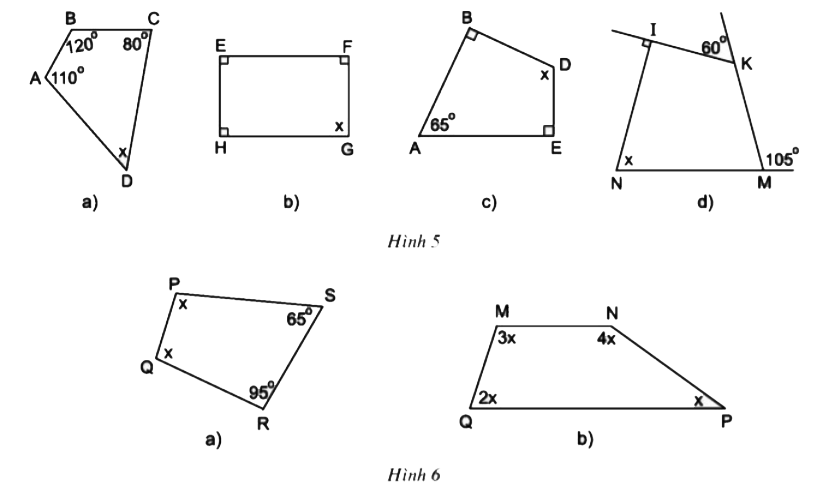
Bài 1 trang 66 SGK Toán 8 tập 1

Hướng dẫn giải:

- Hình 5a): $x = 360^0 – (110^0 + 120^0 + 80^0) = 50^0$

- Hình 5b): $x = 360^0 – (90^0 + 90^0 + 90^0) = 90^0$

- Hình 5c): $x = 360^0 – (90^0 + 65^0 + 90^0) = 115^0$

- Hình 5d): $x = 360^0 – (90^0 + 120^0 + 75^0) = 75^0$

- Hình 6a): $2x = 360^0 – (65^0 + 95^0)$

$⇒ x = \frac{360^0 – (65^0 + 95^0)}{2} = 100^0$ $⇒ x = \frac{360^0 – (65^0 + 95^0)}{2} = 100^0$

- Hình 6b): $x + 2x + 3x + 4x = 360^0$

$⇔ 10x = 360^0 ⇒ x = 36^0$

Bài 2 (trang 66 SGK Toán 8 Tập 1)

Góc kề bù của một góc của tứ giác gọi là góc ngoài của tứ giác.

a) Tính góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = ?$ $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = ?$

c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

Bài 2

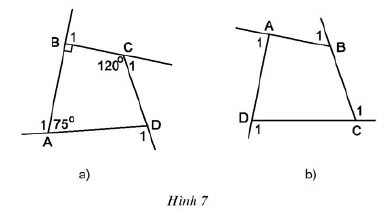
Hướng dẫn giải:

a) Số đo góc còn lại của tứ giác ABCD là:

$\widehat{D} = 360^0 – (90^0 + 120^0 + 75^0) = 75^0$ $\widehat{D} = 360^0 – (90^0 + 120^0 + 75^0) = 75^0$

Góc ngoài của tứ giác tại đỉnh A là:

$\widehat{A_1} = 180^0 – \widehat{A} = 180^0 – 75^0 = 105^0$ $\widehat{A_1} = 180^0 – \widehat{A} = 180^0 – 75^0 = 105^0$

Góc ngoài của tứ giác tại đỉnh B là:

$\widehat{B_1} = 180^0 – \widehat{B} = 180^0 – 90^0 = 90^0$ $\widehat{B_1} = 180^0 – \widehat{B} = 180^0 – 90^0 = 90^0$

Góc ngoài của tứ giác tại đỉnh C là:

$\widehat{C_1} = 180^0 – \widehat{C} = 180^0 – 120^0 = 60^0$ $\widehat{C_1} = 180^0 – \widehat{C} = 180^0 – 120^0 = 60^0$

Góc ngoài của tứ giác tại đỉnh D là:

$\widehat{D_1} = 180^0 – \widehat{D} = 180^0 – 75^0 = 105^0$ $\widehat{D_1} = 180^0 – \widehat{D} = 180^0 – 75^0 = 105^0$

b) Ta có tổng các góc trong của tứ giác ABCD bằng:

$\widehat{A} + \widehat{B} + \widehat{C}+ \widehat{D} = 360^0$ $\widehat{A} + \widehat{B} + \widehat{C}+ \widehat{D} = 360^0$

Tổng các góc ngoài của tứ giác ABCD bằng:

$\widehat{A_1} + \widehat{B_1} + \widehat{C_1} + \widehat{D_1}$ $\widehat{A_1} + \widehat{B_1} + \widehat{C_1} + \widehat{D_1}$

$= (180^0 – \widehat{A}) + (180^0 – \widehat{B}) + (180^0 – \widehat{C}) + (180^0 – \widehat{D})$ $= (180^0 – \widehat{A}) + (180^0 – \widehat{B}) + (180^0 – \widehat{C}) + (180^0 – \widehat{D})$

$= 4 . 180^0 – (\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D})$ $= 4 . 180^0 – (\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D})$

$= 720^0 – 360^0 = 360^0$

c) Như vậy tổng các góc ngoài của tứ giác bằng $360^0$

Bài 3 (trang 67 SGK Toán 8 Tập 1)

Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của BD

b) Tính $\widehat{B}, \widehat{D}$ $\widehat{B}, \widehat{D}$, biết $\widehat{A} = 100^0, \widehat{C} = 60^0$ $\widehat{A} = 100^0, \widehat{C} = 60^0$

Bài 3

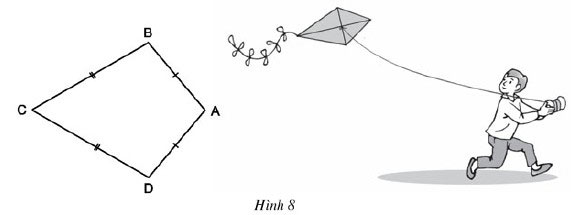
Hướng dẫn giải:

a) Ta có:

AB = AD (gt) ⇒ A thuộc đường trung trực của đoạn thẳng BD

CB = CD (gt) ⇒ C thuộc đường trung trực của đoạn thẳng BD

Nên AC là đường trung trực của đoạn thẳng BD

b) $\Delta ABC$ $\Delta ABC$ và $\Delta ADC$ $\Delta ADC$ có:

$\left.\begin{matrix} Cạnh\: AC\: chung \\ AB = AD (gt) \\ CB = CD (gt) \end{matrix}\right\} ⇒ \Delta ABC = \Delta ADC (c – c – c)$ $\left.\begin{matrix} Cạnh\: AC\: chung \\ AB = AD (gt) \\ CB = CD (gt) \end{matrix}\right\} ⇒ \Delta ABC = \Delta ADC (c – c – c)$

Suy ra $\widehat{B} = \widehat{D} (1)$ $\widehat{B} = \widehat{D} (1)$

Ta lại có:

$\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^0$ $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^0$

$⇔ \widehat{B} + \widehat{D} = 360^0 – (\widehat{A} + \widehat{C})$ $⇔ \widehat{B} + \widehat{D} = 360^0 – (\widehat{A} + \widehat{C})$

$= 360^0 – (100^0 + 60^0) = 200^0 (2)$

Từ (1) và (2) suy ra $\widehat{B} = \widehat{D} = 100^0$ $\widehat{B} = \widehat{D} = 100^0$

Bài 4 (trang 67 SGK Toán 8 Tập 1)

Dựa vào cách vẽ tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở

Bài 4

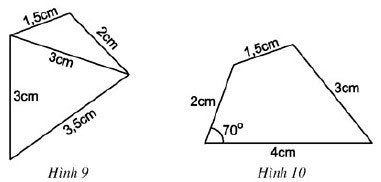
Hướng dẫn giải:

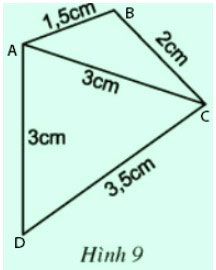
* Vẽ hình 9:

Trước hết vẽ tam giác ABC:

- Dùng thước đó độ dài vẽ đoạn thẳng AC = 3cm

- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm, vẽ cung tròn tâm C bán kính 2cm. Khi đó hai cung tròn cắt nhau tại B

- Nối A với B, C với B ta được tam giác ABC

Tương tự vẽ tam giác ADC:

- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 3cm, vẽ cung tròn tâm C bán kính 3,5cm. Khi đó hai cung tròn cắt nhau tại D

- Nối A với D, C với D ta được tam giác ADC

Tứ giác ABCD là hình cần vẽ.

Bài 4

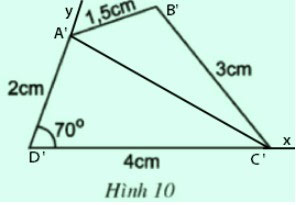
* Vẽ hình 10:

Với hình này ta sẽ vẽ tam giác A’D’C’ trước, bằng cách:

- Dùng thước đo góc vẽ $\widehat{xD’y} = 70^0$ $\widehat{xD’y} = 70^0$

- Trên tia D’x lấy điểm C’ sao cho D’C’ = 4cm

- Trên tia D’y lấy điểm A’ sao cho D’A’ = 2cm

- Vẽ đoạn thẳng A’C’, ta được tam giác A’D’C’

Vẽ tam giác A’B’C’ giống như cách vẽ tam giác ABC ở hình 9:

- Hai cung tròn tâm A’ bán kính 1,5cm và cung tròn tâm C’ bán kính 3cm cắt nhau tại điểm B’

- Vẽ các đoạn thẳng A’B’, B’C’ ta được tam giác A’B’C’

Bài 4

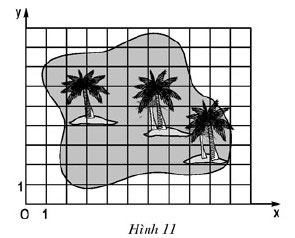
Bài 5 (trang 67 SGK Toán 8 Tập 1)

Đố. Đố em tìm thấy vị trí “kho báu” trên hình 11, biết kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).

Bài 5

Hướng dẫn giải:

Lời giải:

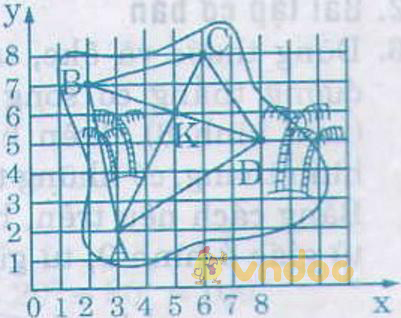
Giải bài tập SGK Toán lớp 8 bài 1: Tứ giác

Đánh dấu các số thứ tự (như trục tọa độ) và kí hiệu các điểm như trên hình. Các bước làm như sau:

- Xác định các điểm A, B, C, D trên hình vẽ với A(3; 2); B(2; 7); C(6; 8); D(8; 5).

- Vẽ tứ giác ABCD

- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.

- Xác định tọa độ của điểm K: K(5; 6)

Vậy vị trí kho báu có tọa độ K(5; 6) trên hình vẽ.

.........................................

Bài tiếp theo: Giải Toán 8 bài 2: Hình thang

Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 1: Tứ giác. Để xem lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải cho các bài tập trong SGK Toán lớp 8 theo từng bài, giúp các em luyện giải Toán 8 hiệu quả.

Ngoài tài liệu trên, mời các bạn tham khảo thêm Toán 8 - Giải Toán 8, Giải vở bài tập Toán 8, và các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 mà chúng tôi đã sưu tầm và chọn lọc. để rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt.

Xem thêm:

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời thầy cô và các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Chia sẻ, đánh giá bài viết

38

40.627

Bài trước

Bài sau