Giải Toán 8 bài 4: Khái niệm Hai tam giác đồng dạng
Giải bài tập Toán 8 bài 4: Hai tam giác đồng dạng
Giải Toán 8 bài 4: Khái niệm Hai tam giác đồng dạng bao gồm phần tóm tắt lý thuyết và hướng dẫn giải chi tiết các bài tập trong SGK Toán 8, nhằm giúp các em học sinh ghi nhớ công thức để từ đó biết vận dụng vào giải quyết các dạng bài tập đi kèm. Mời các em tham khảo.
A. Lý thuyết hai tam giác đồng dạng
1. Định nghĩa
Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:
\(\widehat{A'} = \widehat{A}; \widehat{B'} = \widehat{B}; \widehat{C'}= \widehat{C}\)
\(\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = \dfrac{C'A'}{CA}\)
Kí hiệu: ∆A'B'C' ∆ABC
Tỉ số: \(\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC}= \dfrac{C'A'}{CA} = k\) gọi là tỉ số đồng dạng.
2. Tính chất
Hai tam giác A'B'C' và ABC đồng dạng có một số tính chất:
1) ∆ABC ~ ∆A'B'C'
2) Nếu ∆A'B'C' ~ ∆ABC thì ∆ABC ~ ∆A'B'C'
3) Nếu ∆A'B'C' ~ ∆A"B"C" và ∆A"B"C" ~ ∆ABC thì ∆A'B'C' ~ ∆ABC
3. Định lí
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
4. Chú ý
Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài của hai tam giác song song với cạnh còn lại.
Giải bài tập Toán 8 tập 2 trang 71, 72
Bài 23 trang 71 SGK Toán 8 tập 2
Trong hai mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác đồng dạng với nhau thì bằng nhau.
Hướng dẫn giải:
a) a là mệnh đề đúng.
b) b là mệnh đề sai
Bài 24 trang 72 SGK Toán 8 tập 2
∆A'B'C' ∽ ∆A"B"C" theo tỉ số đồng dạng K1, ∆A"B"C" ∽∆ ABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
Hướng dẫn giải:
∆A'B'C' ∽ ∆A"B"C" theo tỉ số đồng dạng \(k_1=\dfrac{A'B'}{A"B"}\)
∆A"B"C" ∽ ∆ ABC theo tỉ số đồng dạng \(k_2=\dfrac{A"B"}{AB}\)
Theo tính chất 3 của hai tam giác đồng dạng thì ∆A'B'C' ∽ ∆ABC.
Tỉ số đồng dạng \(k= \dfrac{A'B'}{AB} = \dfrac{A'B'.A"B"}{A''B''.AB} = \dfrac{A'B'}{A"B"}.\dfrac{A"B"}{AB}\)
Vậy \(k = k_1.k_2\).
Bài 25 trang 72 SGK Toán 8 tập 2
Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số ½.
Hướng dẫn giải:
Lấy trung điểm M của AB, N là trung điểm của AC => MN là đường trung bình của tam giác ABC.
=> MN // BC.
=> ∆ AMN ∽ ∆ABC theo tỉ số K = ½.
Bài 26 trang 72 SGK Toán 8 tập 2
Cho tam giác ABC vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng là K = 2/3
Hướng dẫn giải:
Trên cạnh AB lấy điểm M sao cho AM = 2/3AB.
Từ M vẽ đường song song với BC cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K = 2/3
Dựng ∆A'B'C' = ∆AMN (theo trường hợp cạnh cạnh cạnh)
Bài 27 trang 72 SGK Toán 8 tập 2
Từ M thuộc cạnh AB của tam giác ABC với AM= 1/2 MB. Kẻ các tia song song với AC, BC. Chúng cắt BC và AC lần lượt tại L và N.
a) Nêu tất cả các cặp tam giác đồng dạng.
b) Đối với mỗi cặp tam giác đồng dang, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.
Hướng dẫn giải:
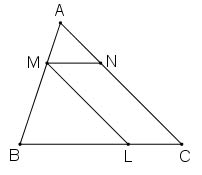
a) Áp dụng: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho, ta có:
\(MN // BC (gt) \Rightarrow ∆AMN ∽ ∆ABC\)
\(ML // AC (gt) \Rightarrow ∆MBL ∽ ∆ABC\)
và ∆AMN ∽ ∆MBL (vì cùng đồng dạng với tam giác ABC)
b)
∆AMN ∽ ∆ABC có:
\(\widehat{AMN} = \widehat{ABC}; \widehat{ANM} = \widehat{ACB}; \widehat{A}\) chung
Tỉ số đồng dạng \(k_1=\dfrac{AM}{AB}= \dfrac{1}{3}\) (vì \(AM=\dfrac{1}{2}MB\))
\(∆MBL ∽ ∆ABC\) có:
\(\widehat{BML} = \widehat{BAC}, \widehat{B}\) chung, \(\widehat{MLB} = \widehat{ACB}\)
Tỉ số đồng dạng \(k_2=\dfrac{MB}{AB}= \dfrac{2}{3}\)
∆AMN ∽ ∆MBL có:
\(\widehat{MAN} = \widehat{BML}, \widehat{AMN} = \widehat{MBL}, \widehat{ANM} = \widehat{MLB}\)
Tỉ số đồng dạng \(k_3=\dfrac{AM}{MB} = \dfrac{1}{2}\)
Bài 28 trang 72 SGK Toán 8 tập 2
∆A'B'C' ∽ ∆ABC theo tỉ số đồng dạng K = 3/5
a) Tính tỉ số chú vi của hai tam giác đã cho.
b) Cho biết chu vi của hai tam giác trên là 40dm, tính chu vi của mỗi tam giác.
Hướng dẫn giải:
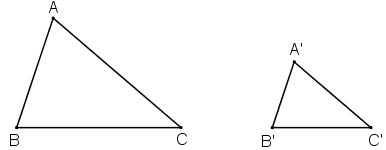
a) ∆A'B'C' ∽ ∆ABC theo tỉ số đồng dạng \(k= \dfrac{3}{5}\) (gt)
\(\Rightarrow \dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = \dfrac{C'A'}{CA} = \dfrac{3}{5}\) (tính chất hai tam giác đồng dạng)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}} = \dfrac{{C'A'}}{{CA}}= \dfrac{A'B'+B'C'+C'A'}{AB+BC+CA}= \dfrac{C_{A'B'C'}}{C_{ABC}}= \dfrac{3}{5}\)
Với \(C_{A'B'C'};C_{ABC}\) lần lượt là chu vi hai tam giác A'B'C';ABC
Vậy tỉ số chu vi của ∆A'B'C' và ∆ABC là \(\dfrac{3}{5}\).
b) Vì \(\dfrac{C_{A'B'C'}}{C_{ABC}}= \dfrac{3}{5}\) suy ra \(\dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3}\) mà \(C_{ABC}- C_{A'B'C'} = 40\,dm\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3} =\dfrac{{{C_{ABC}} - {C_{A'B'C'}}}}{{5 - 3}}= \dfrac{40}{2}= 20\)
\(\Rightarrow C_{ABC}= 5.20=100\, dm\)
\(C_{A'B'C'}= 20.3=60\, dm\)
.............................
Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 4: Khái niệm Hai tam giác đồng dạng. Trong quá trình học môn Toán lớp 8, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã sưu tầm và chọn lọc thêm phần Giải Toán 8 hay Giải Vở BT Toán 8 để giúp các bạn học sinh học tốt hơn.
Ngoài bài tập cơ bản môn Toán lớp 8 chuyên đề này, các bạn học sinh có thể tham khảo thêm các đề thi học kì 2 môn Toán, môn Ngữ Văn, chuẩn bị tốt kiến thức cho kì thi học kì 2 sắp tới.
