Toán 8 Bài 6: Hình thoi

Bài 1 trang 115 Toán 8 Cánh diều tập 1

Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.

Hướng dẫn giải

ABCD là hình bình hành nên:

AD = BC; AB = DC (1)

Xét 2 tam giác ADC và CBA có:

• AC chung
• Kết hợp với (1)

=> 2 tam giác ADC và CBA bằng nhau (c-c-c)=> 2 góc tương ứng \(\widehat{DCA}=\widehat{BAC}\) (2)

Mà AC là tia phân giác của góc DAB => \(\widehat{DAC}=\widehat{BAC}\). Kết hợp với (2) => \(\widehat{DAC}=\widehat{DCA}\)

=> Tam giác DAC cân tại D => DA = DC. Kết hợp với (1) => AD = BC = AB = DC => ABCD có 4 cạnh bằng nhau nên là hình thoi.

Bài 2 trang 115 Toán 8 Cánh diều tập 1

Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh: \(AC^{2}+BD^{2}=4(OA^{2}+OB^{2})=4AB^{2}\)

Hướng dẫn giải

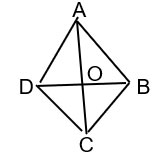
ABCD là hình thoi nên 2 đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường => OA = OC, OB = OD.

\(=> AC^{2}+BD^{2}=(OA+OC)^{2}+(OB+OD)^{2} = (2OA)^{2}+(2OB)^{2}\)

= \(4OA^{2}+4OB^{2} = 4(OA^{2}+OB^{2})\) (1)

Xét tam giác vuông OAB vuông tại O có: \(AB^{2} = OA^{2}+OB^{2}\) (2)

Từ (1) và (2) => \(AC^{2}+BD^{2}=4(OA^{2}+OB^{2})=4AB^{2}\) (đpcm)

Bài 3 trang 115 Toán 8 Cánh diều tập 1

Cho hình thoi ABCD có \(\widehat{CDB}=40^{\circ}\). Tính số đo mỗi góc của hình thoi ABCD.

Hướng dẫn giải

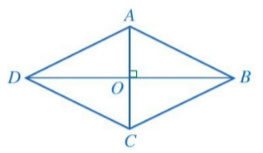
ABCD là hình thoi nên DB là tia phân giác của góc D => \(\widehat{D} = 2. \widehat{CDB}\)= \(2. 40^{\circ} = 80^{\circ}\)

ABCD là hình thoi nên nó cũng là một hình bình hành. Suy ra:

\(\widehat{D} = \widehat{B} = 80^{\circ}\) (2 góc đối nhau)

\(\widehat{A} = \widehat{C} = \frac{1}{2}(360^{\circ}-\widehat{D}-\widehat{B}) = \frac{1}{2}(360^{\circ}-80^{\circ}-80^{\circ})=100^{\circ}\) (2 góc đối nhau)

Bài 4 trang 115 Toán 8 Cánh diều tập 1

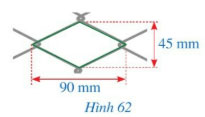
Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mm và 90 mm. Độ dài cạnh của ô lưới mắt cáo đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)?

Hướng dẫn giải

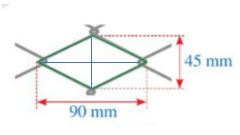
Độ dài cạnh của ô lưới mắt cáo đó là:

\(\sqrt{\left ( \frac{1}{2}.45 \right )^{2}+\left ( \frac{1}{2}.90 \right )^{2}}= 50,3\) (mm)

Bài 6 trang 115 Toán 8 Cánh diều tập 1

Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60° (Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?

Hướng dẫn giải

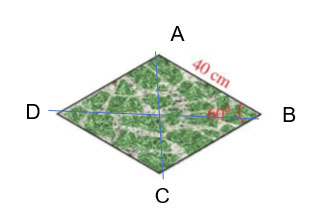
Tam giác ABC có AB = BC (2 cạnh của hình thoi) nên là tam giác cân tại B. Lại có góc B = \(60^{\circ}\) nên ABC là tam giác đều => AC = 40cm.

Gọi O là giao điểm của 2 đường chéo AC và BD. Khi đó: OA = \(\frac{1}{2}\)AC = 20cm.

Trong tam giác AOB có OB = \(\sqrt{AB^{2}-OA^{2}}=\sqrt{40^{2}-20^{2}} = 34,6\) cm

Diện tích tam giác ABC = \(\frac{1}{2}.OB.AC = \frac{1}{2}.34,6.40 = 692\) \(cm^{2}\)

=> Diện tích viên gạch có dạng hình thoi như trên sẽ là: 2. 692 = 1 384\(cm^{2}\)