Toán 8 Cánh diều bài 3 trang 18, 19, 20, 21, 22, 23

Hằng đẳng thức đáng nhớ

Giải Toán 8 Cánh diều bài 3: Hằng đẳng thức đáng nhớ hướng dẫn giải bài tập trong SGK Toán 8 Cánh diều tập 1 trang 18, 19, 20, 21, 22, 23 trang 18, 19, 20, 21, 22, 23. Mời các em cùng tham khảo để nắm được nội dung bài học.

Khởi động trang 18 Toán 8 Tập 1:

Diện tích của hình vuông MNPQ (Hình 4) có thể được tính theo những cách nào?

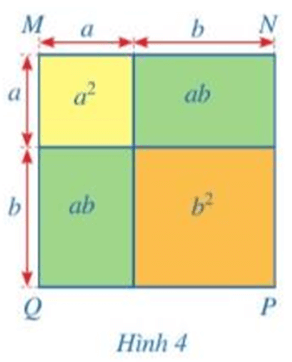
Khởi động trang 18 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Hướng dẫn giải:

Ta đặt tên các điểm A, B, C, D như hình vẽ:

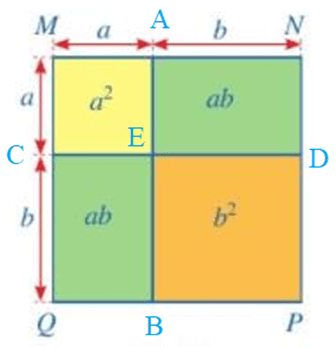
Khởi động trang 18 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Diện tích của hình vuông MNPQ có thể được tính theo những cách sau:

Cách 1. Tính theo tổng diện tích của 4 hình AMCE, ANDE, BEDP, BECQ.

Cách 2. Tính theo tổng diện tích của 2 hình: MNDC, CDPQ.

Cách 3. Tính theo tổng diện tích của 2 hình: ABQM, ABPN.

Cách 4. Tìm độ dài một cạnh của hình vuông MNPQ rồi tính diện tích.

I. Hằng đẳng thức

Hoạt động 1 trang 18 sgk Toán 8 tập 1 CD: Xét hai biểu thức: P = 2(x+y) và Q = 2x+2y. Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:

a. Tại x = 1; y = - 1.

b. Tại x = 2; y = - 3

Bài giải

a. Tại x = 1; y = - 1

P = 2(1-1) = 0

Q = 2.1-2.1 = 0

=> P = Q

b. Tại x = 2; y = - 3

P = 2(2-3) = -2

Q = 2.2+2.(-3) = -2

=> P = Q

Luyện tập 1 trang 18 sgk Toán 8 tập 1 CD: Chứng minh rằng: $x(xy^{2}+y)-y(x^{2}y+x)=0$ $x(xy^{2}+y)-y(x^{2}y+x)=0$

Bài giải

Ta có: $x(xy^{2}+y)-y(x^{2}y+x)$ $x(xy^{2}+y)-y(x^{2}y+x)$

$= x.xy^{2}+xy-x^{2}y.y-xy$ $= x.xy^{2}+xy-x^{2}y.y-xy$

$= x^{2}y^{2}+xy-x^{2}y^{2}-xy = 0 (đpcm)$ $= x^{2}y^{2}+xy-x^{2}y^{2}-xy = 0 (đpcm)$

II. Hằng đẳng thức đáng nhớ

1. Bình phương của một tổng, một hiệu

Hoạt động 2 trang 18 sgk Toán 8 tập 1 CD: Với a,b là 2 số thức bất kì, thực hiện phép tính:

a. (a+b)(a+b)

b. (a-b)(a-b)

Bài giải

$a. (a+b)(a+b) = a.a+a.b+b.a+b.b = a^{2}+2ab+b^{2}$ $a. (a+b)(a+b) = a.a+a.b+b.a+b.b = a^{2}+2ab+b^{2}$

$b. (a-b)(a-b) = a.a-a.b-b.a+b.b = a^{2}-2ab+b^{2}$ $b. (a-b)(a-b) = a.a-a.b-b.a+b.b = a^{2}-2ab+b^{2}$

Luyện tập 2 trang 18 sgk Toán 8 tập 1 CD: Tính:

$a. (x+\frac{1}{2})^{2}$ $a. (x+\frac{1}{2})^{2}$

$b. (2x+y)^{2}$ $b. (2x+y)^{2}$

$c. (3-x)^{2}$ $c. (3-x)^{2}$

$d. (x-4y)^{2}$ $d. (x-4y)^{2}$

Bài giải

$a. (x+\frac{1}{2})^{2} = x^{2}+2.\frac{1}{2}x+(\frac{1}{2})^{2}$ $a. (x+\frac{1}{2})^{2} = x^{2}+2.\frac{1}{2}x+(\frac{1}{2})^{2}$

$= x^{2}+x+\frac{1}{4}$ $= x^{2}+x+\frac{1}{4}$

$b. (2x+y)^{2} = (2x)^{2}+2.2x.y+y^{2}$ $b. (2x+y)^{2} = (2x)^{2}+2.2x.y+y^{2}$

$= 4x^{2}+4xy+y^{2}$ $= 4x^{2}+4xy+y^{2}$

$c. (3-x)^{2} = 3^{2}-2.3.x+x^{2}$ $c. (3-x)^{2} = 3^{2}-2.3.x+x^{2}$

$= 3^{2}-6x+x^{2}$ $= 3^{2}-6x+x^{2}$

$d. (x-4y)^{2} = x^{2}-2.x.4y+(4y)^{2}$ $d. (x-4y)^{2} = x^{2}-2.x.4y+(4y)^{2}$

$= x^{2}-8xy+16y^{2}$ $= x^{2}-8xy+16y^{2}$

Luyện tập 3 trang 18 sgk Toán 8 tập 1 CD: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

$a. y^{2}+y+\frac{1}{4}$ $a. y^{2}+y+\frac{1}{4}$

$b. y^{2}+49-14y$ $b. y^{2}+49-14y$

Bài giải

$a. y^{2}+y+\frac{1}{4} = y^{2}+2.y.\frac{1}{2}+(\frac{1}{2})^{2}$ $a. y^{2}+y+\frac{1}{4} = y^{2}+2.y.\frac{1}{2}+(\frac{1}{2})^{2}$

$= (y+\frac{1}{2})^{2}$ $= (y+\frac{1}{2})^{2}$

$b. y^{2}+49-14y = y^{2}-14y+49$ $b. y^{2}+49-14y = y^{2}-14y+49$

$= y^{2}-2.y.7+7^{2} = (y-7)^{2}$ $= y^{2}-2.y.7+7^{2} = (y-7)^{2}$

Luyện tập 4 trang 18 sgk Toán 8 tập 1 CD: Tính nhanh $49^{2}$ $49^{2}$

Bài giải

$49^{2}= (50-1)^{2}$ $49^{2}= (50-1)^{2}$

$= 50^{2}-2.50.1+1^{2}$ $= 50^{2}-2.50.1+1^{2}$

$= 2 500 - 100+ 1 = 2401$

Luyện tập 5 trang 20 sgk Toán 8 tập 1 CD: Viết biểu thức sau dưới dạng tích:

$a. 9x^{2}-16$ $a. 9x^{2}-16$

$b. 25-16y^{2}$ $b. 25-16y^{2}$

Bài giải

$a. 9x^{2}-16 = (3x)^{2}-4^{2}$ $a. 9x^{2}-16 = (3x)^{2}-4^{2}$

$= (3x-4)(3x+4)$

$b. 25-16y^{2} = 5^{2}-(4y)^{2}$ $b. 25-16y^{2} = 5^{2}-(4y)^{2}$

$= (5-4y)(5+4y)$

Luyện tập 6 trang 20 sgk Toán 8 tập 1 CD: Tính:

$a. (a-3b) (a+3b)$

$b. (2x-5) (2x+5)$

$c. (4y-1) (4y+1)$

Bài giải

$a. (a-3b) (a+3b) = a^{2}-(3b)^{2} = a^{2}-9b^{2}$ $a. (a-3b) (a+3b) = a^{2}-(3b)^{2} = a^{2}-9b^{2}$

$b. (2x-5) (2x+5) = (2x)^{2}-5^{2} = 4x^{2}-25$ $b. (2x-5) (2x+5) = (2x)^{2}-5^{2} = 4x^{2}-25$

$c. (4y-1) (4y+1) = (4y)^{2}-1^{2} = 16y^{2}-1$ $c. (4y-1) (4y+1) = (4y)^{2}-1^{2} = 16y^{2}-1$

Luyện tập 7 trang 20 sgk Toán 8 tập 1 CD: Tính nhanh 48.52

Bài giải

$48 . 52 = (50-2)(50+2) = 50^{2}-2^{2} = 2 500 - 4 = 2496$ $48 . 52 = (50-2)(50+2) = 50^{2}-2^{2} = 2 500 - 4 = 2496$

3. Lập phương của một tổng, một hiệu

Hoạt động 4 trang 20 sgk Toán 8 tập 1 CD: Với a,b là 2 số thực bát kì, thực hiện phép tính:

$a. (a+b)(a+b)^{2}.$ $a. (a+b)(a+b)^{2}.$

$b. (a-b)(a-b)^{2}.$ $b. (a-b)(a-b)^{2}.$

Bài giải

$a. (a+b)(a+b)^{2}$ $a. (a+b)(a+b)^{2}$

$= (a+b)(a^{2}+2ab+b^{2})$ $= (a+b)(a^{2}+2ab+b^{2})$

$= a.a^{2}+2.a.ab+a.b^{2}+b.a^{2}+b.2ab+b.b^{2}$ $= a.a^{2}+2.a.ab+a.b^{2}+b.a^{2}+b.2ab+b.b^{2}$

$= a^{3}+2a^{2}b+ab^{2}+a^{2}b+2ab^{2}+b^{3}$ $= a^{3}+2a^{2}b+ab^{2}+a^{2}b+2ab^{2}+b^{3}$

$= a^{3}+3a^{2}b+3ab^{2}+b^{3}$ $= a^{3}+3a^{2}b+3ab^{2}+b^{3}$

$b. (a-b)(a-b)^{2}$ $b. (a-b)(a-b)^{2}$

$= (a-b)(a^{2}-2ab+b^{2})$ $= (a-b)(a^{2}-2ab+b^{2})$

$= a.a^{2}-2.a.ab+a.b^{2}-b.a^{2}+b.2ab-b.b^{2}$ $= a.a^{2}-2.a.ab+a.b^{2}-b.a^{2}+b.2ab-b.b^{2}$

$= a^{3}-2a^{2}b+ab^{2}-a^{2}b+2ab^{2}-b^{3}$ $= a^{3}-2a^{2}b+ab^{2}-a^{2}b+2ab^{2}-b^{3}$

$= a^{3}-3a^{2}b+3ab^{2}-b^{3}$ $= a^{3}-3a^{2}b+3ab^{2}-b^{3}$

Luyện tập 8 trang 21 sgk Toán 8 tập 1 CD: Tính:

$a. (3+x)^{3}$ $a. (3+x)^{3}$

$b. (a+2b)^{3}$ $b. (a+2b)^{3}$

$c. (2x-y)^{3}$ $c. (2x-y)^{3}$

Bài giải

$a. (3+x)^{3}$ $a. (3+x)^{3}$

$= 3^{3}+3.3^{2}x+3.3.x^{2}+x^{3}$ $= 3^{3}+3.3^{2}x+3.3.x^{2}+x^{3}$

$= x^{3}+9x^{2}+27x+27$ $= x^{3}+9x^{2}+27x+27$

$b. (a+2b)^{3}$ $b. (a+2b)^{3}$

$= a^{3}+3.a^{2}.2b+3.a.(2b)^{2}+(2b)^{3}$ $= a^{3}+3.a^{2}.2b+3.a.(2b)^{2}+(2b)^{3}$

$= a^{3}+6a^{2}b+12ab^{2}+8b^{3}$ $= a^{3}+6a^{2}b+12ab^{2}+8b^{3}$

$c. (2x-y)^{3}$ $c. (2x-y)^{3}$

$=(2x)^{3}-3.(2x)^{2}.y+3.2x.y^{2}-b^{3}$ $=(2x)^{3}-3.(2x)^{2}.y+3.2x.y^{2}-b^{3}$

$= 8x^{3}-3.4x^{2}.y+6x.y^{2}-b^{3}$ $= 8x^{3}-3.4x^{2}.y+6x.y^{2}-b^{3}$

$= 8x^{3}-12x^{2}y+6xy^{2}-b^{3}$ $= 8x^{3}-12x^{2}y+6xy^{2}-b^{3}$

Luyện tập 9 trang 21 sgk Toán 8 tập 1 CD: Viết biểu thức sau dưới dạng lập phương của một hiệu: $8x^{3}-36x^{2}y+54xy^{2}-27y^{3}$ $8x^{3}-36x^{2}y+54xy^{2}-27y^{3}$

Bài giải

$8x^{3}-36x^{2}y+54xy^{2}-27y^{3}$ $8x^{3}-36x^{2}y+54xy^{2}-27y^{3}$

$= (2x)^{3}-3.(2x)^{2}.3y+3.2x.(3y)^{2}-(3y)^{3}$ $= (2x)^{3}-3.(2x)^{2}.3y+3.2x.(3y)^{2}-(3y)^{3}$

$= (2x-3y)^{3}$ $= (2x-3y)^{3}$

Luyện tập 10 trang 21 sgk Toán 8 tập 1 CD: Tính nhanh: $101^{3}-3.101^{2}+3.101-1$ $101^{3}-3.101^{2}+3.101-1$

Bài giải

$101^{3}-3.101^{2}+3.101-1$ $101^{3}-3.101^{2}+3.101-1$

$= 101^{3}-3.101^{2}.1+3.101.1^{2}-1^{3}$ $= 101^{3}-3.101^{2}.1+3.101.1^{2}-1^{3}$

$= (101-1)^{3} = 100^{3}$ $= (101-1)^{3} = 100^{3}$

= 1 000 000

4. Tổng, hiệu hai lập phương

Hoạt động 5 trang 21 sgk Toán 8 tập 1 CD: Với a, b là hai số thực bất kì, thực hiện phép tính:

$a. (a+b)(a^{2}-ab+b^{2}).$ $a. (a+b)(a^{2}-ab+b^{2}).$

$b. (a-b)(a^{2}+ab+b^{2}).$ $b. (a-b)(a^{2}+ab+b^{2}).$

Bài giải

$a. (a+b)(a^{2}-ab+b^{2})$ $a. (a+b)(a^{2}-ab+b^{2})$

$= a.a^{2}-a.ab+a.b^{2}+b.a^{2}-b.ab+b^{3}$ $= a.a^{2}-a.ab+a.b^{2}+b.a^{2}-b.ab+b^{3}$

$= a^{3}-a^{2}b+ab^{2}+a^{2}b-ab^{2}+b^{3}$ $= a^{3}-a^{2}b+ab^{2}+a^{2}b-ab^{2}+b^{3}$

$= a^{3}+b^{3}$ $= a^{3}+b^{3}$

$b. (a-b)(a^{2}+ab+b^{2})$ $b. (a-b)(a^{2}+ab+b^{2})$

$= a.a^{2}+a.ab+a.b^{2}-b.a^{2}-b.ab-b^{3}$ $= a.a^{2}+a.ab+a.b^{2}-b.a^{2}-b.ab-b^{3}$

$= a^{3}+a^{2}b+ab^{2}-a^{2}b-ab^{2}-b^{3}$ $= a^{3}+a^{2}b+ab^{2}-a^{2}b-ab^{2}-b^{3}$

$= a^{3}-b^{3}$ $= a^{3}-b^{3}$

Luyện tập 11 trang 22 sgk Toán 8 tập 1 CD: Viết mỗi biểu thức sau dưới dạng tích:

$a. 27x^{3}+1$ $a. 27x^{3}+1$

$b. 64-8y^{3}$ $b. 64-8y^{3}$

Bài giải

Viết mỗi biểu thức sau dưới dạng tích:

$a. 27x^{3}+1 = (3x)^{3}+1^{3}=(3x+1)((3x)^{2}-3x.1+1^{2})$ $a. 27x^{3}+1 = (3x)^{3}+1^{3}=(3x+1)((3x)^{2}-3x.1+1^{2})$

$=(3x+1)(9x^{2}-3x+1)$ $=(3x+1)(9x^{2}-3x+1)$

$b. 64-8y^{3} = 4^{3}-8y^{3}$ $b. 64-8y^{3} = 4^{3}-8y^{3}$

$= (4-8y)(4^{2}+4.8y+(8y)^{2}) = (4-8y)(16+32y+64y^{2})$ $= (4-8y)(4^{2}+4.8y+(8y)^{2}) = (4-8y)(16+32y+64y^{2})$

III. Bài tập

Bài tập 1 trang 23 sgk Toán 8 tập 1 CD: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

$a. 4x^{2}+28x+49$ $a. 4x^{2}+28x+49$

$b. 4a^{2}+20ab+25b^{2}$ $b. 4a^{2}+20ab+25b^{2}$

$c. 16^{2}-8y+1$ $c. 16^{2}-8y+1$

$d. 9x^{2}-6xy+y^{2}$ $d. 9x^{2}-6xy+y^{2}$

Bài giải

Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

$a. 4x^{2}+28x+49 = (2x)^{2}+2.2x.7+7^{2} = (2x+7)^{2}$ $a. 4x^{2}+28x+49 = (2x)^{2}+2.2x.7+7^{2} = (2x+7)^{2}$

$b. 4a^{2}+20ab+25b^{2} = (2a)^{2}+2.2a.5b+(5b)^{2}=(2a+5b)^{2}$ $b. 4a^{2}+20ab+25b^{2} = (2a)^{2}+2.2a.5b+(5b)^{2}=(2a+5b)^{2}$

$c. 16^{2}-8y+1 = (4y)^{2}-2.4y.1+1^{2}=(4y-1)^{2}$ $c. 16^{2}-8y+1 = (4y)^{2}-2.4y.1+1^{2}=(4y-1)^{2}$

$d. 9x^{2}-6xy+y^{2} = (3x)^{2}-2.3x.y+y^{2}=(3x-y)^{2}$ $d. 9x^{2}-6xy+y^{2} = (3x)^{2}-2.3x.y+y^{2}=(3x-y)^{2}$

Bài tập 2 trang 23 sgk Toán 8 tập 1 CD: Viết các biểu thức sau đây dưới dạng lập phương của một tổng hoặc một hiệu

$a. a^{3}+12a^{2}+48a+64$ $a. a^{3}+12a^{2}+48a+64$

$b. 27x^{3}+54x^{2}y+36xy^{2}+8y^{3}$ $b. 27x^{3}+54x^{2}y+36xy^{2}+8y^{3}$

$c. x^{3}-9x^{2}y+27x-27$ $c. x^{3}-9x^{2}y+27x-27$

$d. 8a^{3}-12a^{2}b+6ab^{2}-b^{3}$ $d. 8a^{3}-12a^{2}b+6ab^{2}-b^{3}$

Bài giải

$a. a^{3}+12a^{2}+48a+64$ $a. a^{3}+12a^{2}+48a+64$

$= a^{3}+3.a^{2}.4+3.a.4^{2}+4^{3}$ $= a^{3}+3.a^{2}.4+3.a.4^{2}+4^{3}$

$= (a+4)^{3}$ $= (a+4)^{3}$

$b. 27x^{3}+54x^{2}y+36xy^{2}+8y^{3}$ $b. 27x^{3}+54x^{2}y+36xy^{2}+8y^{3}$

$= (3x)^{3}+3.(3x)^{2}.2y+3.3x.(2y)^{2}+(2y)^{3}$ $= (3x)^{3}+3.(3x)^{2}.2y+3.3x.(2y)^{2}+(2y)^{3}$

$= (3x+2y)^{3}$ $= (3x+2y)^{3}$

$c. x^{3}-9x^{2}y+27x-27$ $c. x^{3}-9x^{2}y+27x-27$

$= x^{3}-3.x^{2}.3+3.x.3^{2}+3^{3}$ $= x^{3}-3.x^{2}.3+3.x.3^{2}+3^{3}$

$= (x-3)^{3}$ $= (x-3)^{3}$

$d. 8a^{3}-12a^{2}b+6ab^{2}-b^{3}$ $d. 8a^{3}-12a^{2}b+6ab^{2}-b^{3}$

$= (2a)^{3}-3.(2a)^{2}b+3.2a.b^{2}-b^{3}$ $= (2a)^{3}-3.(2a)^{2}b+3.2a.b^{2}-b^{3}$

$= (2a-b)^{3}$ $= (2a-b)^{3}$

Bài tập 3 trang 23 sgk Toán 8 tập 1 CD: Viết mỗi biểu thức sau dưới dạng tích:

$a. 25x^{2}-16$ $a. 25x^{2}-16$

$b. 16a^{2}-9b^{2}$ $b. 16a^{2}-9b^{2}$

$c. 8x^{3}+1$ $c. 8x^{3}+1$

$d. 125x^{3}+27y^{3}$ $d. 125x^{3}+27y^{3}$

$e. 8x^{3}-125$ $e. 8x^{3}-125$

$g. 27x^{3}-y^{3}$ $g. 27x^{3}-y^{3}$

Bài giải

$a. 25x^{2}-16$ $a. 25x^{2}-16$

$=(5x)^{2}-4^{2}$ $=(5x)^{2}-4^{2}$

$=(5x-4)(5x+4)$

$b. 16a^{2}-9b^{2}$ $b. 16a^{2}-9b^{2}$

$= (4a)^{2}-(3b)^{2}$ $= (4a)^{2}-(3b)^{2}$

$= (4a-3b)(4a+3b)$

$c. 8x^{3}+1$ $c. 8x^{3}+1$

$= (2x)^{3}+1^{3}$ $= (2x)^{3}+1^{3}$

$= (2x+1)((2x)^{2}-2x.1+1^{2})$ $= (2x+1)((2x)^{2}-2x.1+1^{2})$

$= (2x+1)(4x^{2}-2x+1)$ $= (2x+1)(4x^{2}-2x+1)$

$d. 125x^{3}+27y^{3}$ $d. 125x^{3}+27y^{3}$

$= (5x)^{3}+(3y)^{3}$ $= (5x)^{3}+(3y)^{3}$

$= (5x+3y)((5x)^{2}-5x.3y+(3y)^{2})$ $= (5x+3y)((5x)^{2}-5x.3y+(3y)^{2})$

$= (5x+3y)(25x^{2}-15xy+9y^{2})$ $= (5x+3y)(25x^{2}-15xy+9y^{2})$

$e. 8x^{3}-125$ $e. 8x^{3}-125$

$= (2x)^{3}-5^{3}$ $= (2x)^{3}-5^{3}$

$=(2x-5)((2x)^{2}+2x.5+5^{2})$ $=(2x-5)((2x)^{2}+2x.5+5^{2})$

$=(2x-5)(4x^{2}+10x+25)$ $=(2x-5)(4x^{2}+10x+25)$

$g. 27x^{3}-y^{3}$ $g. 27x^{3}-y^{3}$

$= (3x)^{3}-y^{3}$ $= (3x)^{3}-y^{3}$

$= (3x-y)((3x)^{2}+3x.y+y^{2})$ $= (3x-y)((3x)^{2}+3x.y+y^{2})$

$= (3x-y)(9x^{2}+3xy+y^{2})$ $= (3x-y)(9x^{2}+3xy+y^{2})$

Bài tập 4 trang 23 sgk Toán 8 tập 1 CD: Tính giá trị của mỗi biểu thức:

$a. A = x^{2}+6x+10$ $a. A = x^{2}+6x+10$. tại x = -103

$b. B = x^{3}+6x^{2}+12x+12$ $b. B = x^{3}+6x^{2}+12x+12$ tại x = 8

Bài giải

$a. A = x^{2}+6x+10 = x^{2}+2.x.3+3^{2}+1=(x+3)^{2}+1$ $a. A = x^{2}+6x+10 = x^{2}+2.x.3+3^{2}+1=(x+3)^{2}+1$

Tại x = -103 thì $A = (x+3)^{2}+1 = (-103+3)^{2}+1 = (-100)^{2}+1 = 10 001$ $A = (x+3)^{2}+1 = (-103+3)^{2}+1 = (-100)^{2}+1 = 10 001$

$b. B = x^{3}+6x^{2}+12x+12 = x^{3}+3.x^{2}.2+3.x.2^{2}+2^{3}+4=(x+2)^{3}+4$ $b. B = x^{3}+6x^{2}+12x+12 = x^{3}+3.x^{2}.2+3.x.2^{2}+2^{3}+4=(x+2)^{3}+4$

Tại x = 8 thì $B = (x+2)^{3}+4 = (8+2)^{3}+4 = 1 004$ $B = (x+2)^{3}+4 = (8+2)^{3}+4 = 1 004$

Bài tập 5 trang 23 sgk Toán 8 tập 1 CD: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x.

$a. C= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$ $a. C= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

$b. D = (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$ $b. D = (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$

$c. E = (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$ $c. E = (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

$d. G = (2x-1)(4x^{2}+2x+1)-8(x+2)(x^{2}-2x+4)$ $d. G = (2x-1)(4x^{2}+2x+1)-8(x+2)(x^{2}-2x+4)$

Bài giải

a.

$C= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$ $C= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

$= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$ $= (3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

$=(3x-1)^{2}-2(3x-1)(3x+1)+(3x+1)^{2}$ $=(3x-1)^{2}-2(3x-1)(3x+1)+(3x+1)^{2}$

$= (3x-1-3x-1)^{2}$ $= (3x-1-3x-1)^{2}$

$= (-2)^{2}$ $= (-2)^{2}$

=4.

Giá trị của biểu thức C luôn luôn bằng 4 với mọi x

b.

$D = (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$ $D = (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$

$= (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$ $= (x+2)^{3}-(x-2)^{3}-12(x^{2}+1)$

$= (x^{3}+3.x^{2}.2+3.x.2^{2}+2^{3})-(x^{3}-3.x^{2}.2+3.x.2^{2}-2^{3})-12x^{2}-12$ $= (x^{3}+3.x^{2}.2+3.x.2^{2}+2^{3})-(x^{3}-3.x^{2}.2+3.x.2^{2}-2^{3})-12x^{2}-12$

$= x^{3}+6x^{2}+12.x+2^{3}-x^{3}+6x^{2}-12x+8-12x^{2}-12=-4$ $= x^{3}+6x^{2}+12.x+2^{3}-x^{3}+6x^{2}-12x+8-12x^{2}-12=-4$

Giá trị của biểu thức D luôn luôn bằng -4 với mọi x

c.

$E = (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$ $E = (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

$= (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$ $= (x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

$= (x.x^{2}-x.3x+9x+3x^{2}-9x+27)-(x.x^{2}+x.2x+4x-2x^{2}-2.2x-2.4)$ $= (x.x^{2}-x.3x+9x+3x^{2}-9x+27)-(x.x^{2}+x.2x+4x-2x^{2}-2.2x-2.4)$

$= (x^{3}-3x^{2}+9x+3x^{2}-9x+27)-(x^{3}+2x^{2}+4x-2x^{2}-4x-8)$ $= (x^{3}-3x^{2}+9x+3x^{2}-9x+27)-(x^{3}+2x^{2}+4x-2x^{2}-4x-8)$

$=(x^{3}+27)-(x^{3}-8)$ $=(x^{3}+27)-(x^{3}-8)$

$= x^{3}+27-x^{3}+8$ $= x^{3}+27-x^{3}+8$

= 35

Giá trị của biểu thức E luôn luôn bằng 35 với mọi x

d.