Toán 8 Kết nối tri thức Bài tập cuối chương IV

Giải Toán 8 Kết nối tri thức Bài tập cuối chương IV hướng dẫn giải bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 89, giúp các em nắm vững kiến thức được học trong bài, luyện giải bài tập môn Toán lớp 8. Mời các em cùng tham khảo để nắm được nội dung bài học.

A. Trắc nghiệm

Bài tập 4.18 trang 89 sgk Toán 8 tập 1 KNTT:

Độ dài x trong Hình 4.31 bằng

A. 2,75

B. 2

C. 2,25

D. 3,75

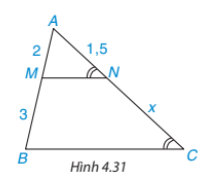
Hướng dẫn giải:

\(\widehat{ANM}=\widehat{NCB}\) mà hai góc ở vị trí so le trong suy ra MN // BC

\(\Rightarrow \frac{AM}{MB}=\frac{AN}{NC}\)

\(\Rightarrow \frac{2}{3}=\frac{1,5}{x}\Rightarrow x=2,25\)

Đáp án: C

Bài tập 4.19 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm

B. 7 cm

C. 10 cm

D. 15 cm

Hướng dẫn giải:

H, K lần lượt là trung điểm của AC, BC suy ra HK là đường trung bình của tam giác ABC

Ta có: AB = 2HK = 2 x 3,5 =7 (cm)

Đáp án: B

Bài tập 4.20 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm

B. 64 cm

C. 30 cm

D. 16 cm

Hướng dẫn giải:

Vì M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC nên MN, NP, MP là các đường trung bình của tam giác ABC

\(\Rightarrow MN=\frac{1}{2}BC;NP=\frac{1}{2}AB,MP=\frac{1}{2}AC\)

\(\Rightarrow MN+NP+MP=\frac{1}{2}BC+\frac{1}{2}AB+\frac{1}{2}AC\)

\(\Leftrightarrow MN+NP+MP=\frac{1}{2}(BC+AB+AC\)

Hay chu vi tam giác MNP =\(\frac{1}{2}\) chu vi tam giác ABC

Do đó chu vi tam giác MNP là: 32 : 2 =16 (cm)

Đáp án: D

Bài tập 4.21 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng

A. 4 cm

B. 5 cm

C. 6 cm

D. 7 cm

Hướng dẫn giải:

Áp dụng định lý Thales:

Với EF // CD ta có \(\frac{AF}{AD}=\frac{AE}{AC}\)

Với DE // BC ta có  \(\frac{AE}{AC}=\frac{AD}{AB}\)

Suy ra \(\frac{AF}{AD}=\frac{AD}{AB} ,\) \(\frac{AF}{6}=\frac{6}{9}\)tức là

Vậy AF = 6x6 :9  = 4 cm

Đáp án: A

Bài tập 4.22 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm

B. 6 cm

C. 9 cm

D. 12 cm

Hướng dẫn giải:

Vì BD là đường phân giác của \(\widehat{ABC}\) nên \(\frac{AD}{DC}=\frac{AB}{BC}\)

Suy ra \(\frac{AD}{DC+AD}=\frac{AB}{BC+AB}\) (theo tính chất dãy tỉ số bằng nhau)

\(\Rightarrow \frac{AD}{AC}=\frac{AB}{BC+AB}\)

Mà tam giác ABC cân tại A nên AC = AB = 15 cm

\(\Rightarrow \frac{AD}{15}=\frac{15}{15+10} \Rightarrow AD=\frac{15 \times 15}{25}=9\) (cm)

Đáp án: C

B. Tự luận

Bài tập 4.23 trang 89 sgk Toán 8 tập 1 KNTT:

Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với Ac cắt Oy tại D. Tính độ dài đonạ thẳng CD.

Hướng dẫn giải:

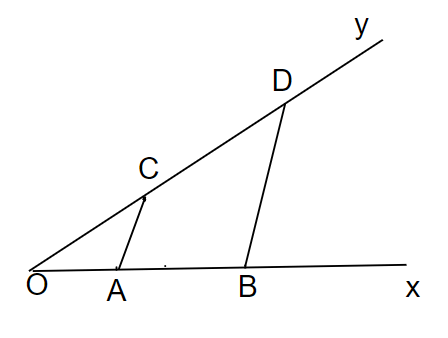
Vì AC // BD, theo định lí Thales ta có:

\(\frac{OC}{CD}=\frac{OA}{AB}\)

hay \(\frac{3}{CD}=\frac{2}{3} \Rightarrow CD=\frac{3 \times 3}{2}=4,5\)(cm)

Bài tập 4.24 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

a) Chứng minh rằng AE = DF

b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng

Hướng dẫn giải:

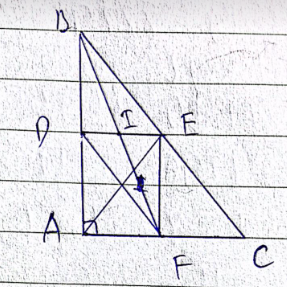
a) D, E, F lần lượt là trung điểm của AB, BC, AC suy ra DE, EF là đường trung bình của tam giác ABC

\(\Rightarrow DE//AC, EF//AB\)

Mà \(AB\perp AC\Rightarrow  DE\perp AB, EF\perp AC\)

Xét tứ giác ADEF có: \(\widehat{ADE}=\widehat{AFE}=\widehat{DAF}=90^{\circ}\)

Do đó ADEF là hình chữ nhật suy ra AE = DF (2 đường chéo)

b) Xét tứ giác DBEF có: DB// EF, BE // DF suy ra DBEF là hình bình hành

I là trung điểm của DE nên I cũng là trung điểm của BF

Vậy ba điểm B, I, F thẳng hàng

Bài tập 4.25 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành

Hướng dẫn giải:

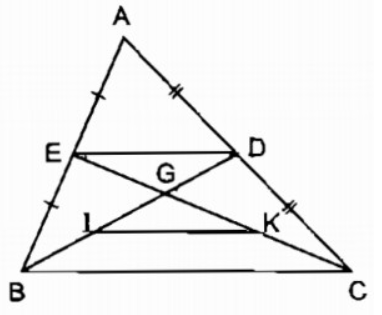
Xét tam giác ABC có: E, D lần lượt là trung điểm AB và AC  suy ra ED là đường trung bình của tam giác ABC

\(\Rightarrow ED//BC, ED=\frac{1}{2}BC\) (1)

Xét tam giác GBC có: I, K lần lượt là trung điểm AB và AC  suy ra IK là đường trung bình của tam giác GBC

\(\Rightarrow IK//BC, IK=\frac{1}{2}BC\) (2)

Từ (1) (2) suy ra ED// IK, ED = IK ⇒ EDKI là hình bình hành

Bài tập 4.26 trang 89 sgk Toán 8 tập 1 KNTT:

Cho tam giác ABC, Điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB). Chứng minh MN song song BC.

Hướng dẫn giải:

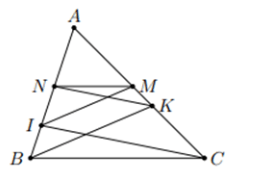
Theo định lí Thales ta có:

\(\frac{AN}{AI}=\frac{AK}{AC};\frac{AI}{AB}=\frac{AM}{AK}\)

\(\Rightarrow AN\times AC=AI\times AK=AB\times AM\)

Suy ra \(\frac{AN}{AB}=\frac{AM}{AC}\)

Do đó theo định lí Thales đảo ta có MN // BC

Bài tập 4.27 trang 89 sgk Toán 8 tập 1 KNTT:

Bác Mến muốn tính khoảng cách giữa hai vị trí P và Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

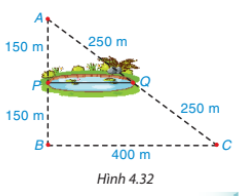
Hướng dẫn giải:

Ta có: AP = PB suy ra P là trung điểm AB

AQ = QC suy ra Q là trung điểm AC

Do đó PQ là đường trung bình tam giác ABC \(\Rightarrow PQ=\frac{1}{2}BC=\frac{1}{2}\times 400=200(m)\)