VnDoc.com

Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác

Giải Toán 8 Kết nối tri thức tập 2

Bài trước

Tải về

Bài sau

Lớp: Lớp 8

Môn: Toán

Dạng tài liệu: Giải bài tập

Bộ sách: Kết nối tri thức với cuộc sống

Loại File: PDF

Phân loại: Tài liệu Tính phí

Giải Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác cung cấp hướng dẫn chi tiết giúp học sinh hiểu rõ nội dung bài học trong SGK Toán 8 Kết nối tri thức, tập 2. Thông qua việc phân tích lý thuyết kết hợp với các ví dụ minh họa và lời giải cụ thể, bài học giúp các em nắm vững ba trường hợp đồng dạng của hai tam giác và biết cách vận dụng vào giải bài tập. Tài liệu này hỗ trợ học sinh rèn luyện tư duy hình học, nâng cao kỹ năng giải Toán 8, từ đó học tập môn Toán hiệu quả và tự tin hơn.

Giải Toán 8 KNTT Bài 34: Ba trường hợp đồng dạng của hai tam giác

HĐ2 trang 85 Toán 8 Tập 2
Câu hỏi trang 86 Toán 8 Tập 2
Luyện tập 2 trang 87 Toán 8 Tập 2
Tranh luận trang 87 Toán 8 Tập 2
HĐ3 trang 88 Toán 8 Tập 2
HĐ4 trang 88 Toán 8 Tập 2
Câu hỏi trang 89 Toán 8 Tập 2:
Luyện tập 3 trang 89 Toán 8 Tập 2
Thử thách nhỏ trang 90 Toán 8 Tập 2:
Bài 9.5 trang 90 Toán 8 KNTT tập 2
Bài 9.6 trang 90 Toán 8 KNTT tập 2
Bài 9.7 trang 90 Toán 8 KNTT tập 2
Bài 9.8 trang 90 Toán 8 KNTT tập 2
Bài 9.9 trang 90 Toán 8 KNTT tập 2
Bài 9.10 trang 90 Toán 8 KNTT tập 2

HĐ2 trang 85 Toán 8 Tập 2

Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng $\widehat A = \widehat {A'} = 60^0$

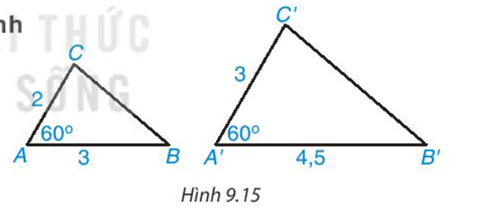
- So sánh các tỉ số $\frac{{A'B'}}{{AB}}{;^{}}\frac{{A'C'}}{{AC}}$

- Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số $\frac {B′C′} {BC}$

- Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?

Hướng dẫn giải

- Có $\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{3}{2}$

- Có $\frac{{B'C'}}{{BC}} = \frac{3}{2}$

- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số $\frac{3}{2}$

Câu hỏi trang 86 Toán 8 Tập 2

Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

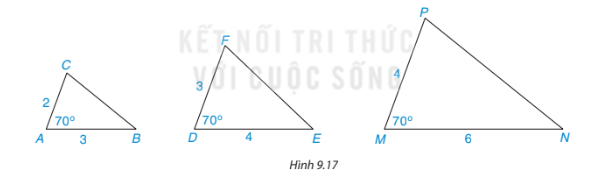
Hướng dẫn giải

Các cặp tam giác đồng dạng: $\Delta ACB \backsim \Delta MPN$

Luyện tập 2 trang 87 Toán 8 Tập 2

Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho $\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}$ . Chứng minh rằng ΔA'B'M' ∽ ΔABM

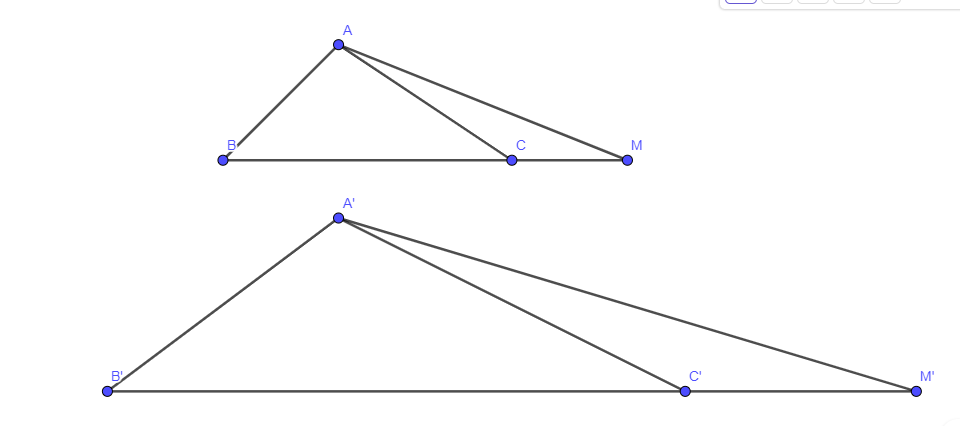
Hướng dẫn giải

Ta có:

$\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\\ \Rightarrow \frac{{MB - BC}}{{MB}} = \frac{{M'B' - B'C'}}{{M'B'}}\\ \Rightarrow 1 - \frac{{BC}}{{MB}} = 1 - \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{M'B'}}{{MB}} = \frac{{B'C'}}{{BC}}(1)\end{array}$

Vì ΔA'B'C' ∽ ΔABC suy ra:

$\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}(2)\end{array}$

Từ (1) và (2) suy ra:

$\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}$

Xét tam giác ABM và tam giác A”B”M’ có:

$\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\end{array}$

Suy ra $\Delta A'B'M' \backsim \Delta ABM$

Tranh luận trang 87 Toán 8 Tập 2

Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có $\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}$ và $\widehat {B'} = \widehat B$ thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?

Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho $\Delta AMC$ cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.

Hướng dẫn giải

Khi góc ACB là góc tù, lấy điểm M trên tia BC sao cho tam giác AMC cân tại A nên AM = AC

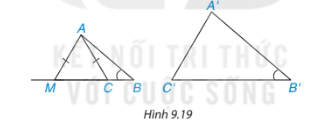
Khi đó $\Delta A'B'C' \backsim \Delta ABM$

Như vậy nhận xét của Lan không chính xác.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3 trang 88 Toán 8 Tập 2

Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, $\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}$ và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, $\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}$ (H.9.20b)

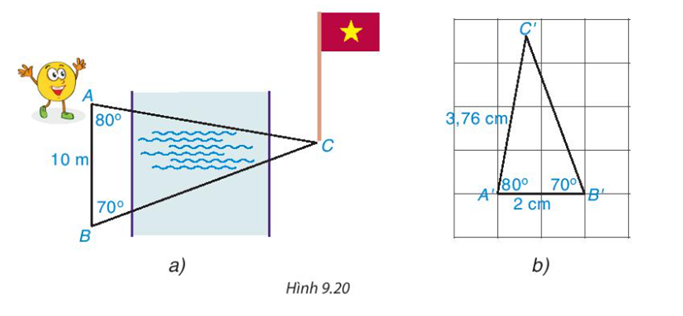
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu

Hướng dẫn giải

Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng $\frac{1}{5}$

HĐ4 trang 88 Toán 8 Tập 2

Nếu ΔABC ∽ ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?

Hướng dẫn giải

Có ΔA'B'C' ∽ ΔABC với tỉ số đồng dạng là $\frac{1}{5}$

$\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{5}$

mà A′C′=3,76 (m) => AC=18,8 (m)

Khoảng cách từ bạn Tròn đến chân cột cờ là 18,8 m.

Câu hỏi trang 89 Toán 8 Tập 2:

Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng

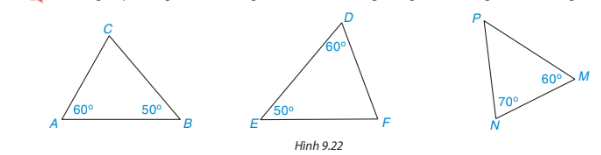
Hướng dẫn giải

Xét tam giác MPN có: $\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}$

Các cặp tam giác đồng dạng trong hình 9.22 là: $\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN$

Luyện tập 3 trang 89 Toán 8 Tập 2

Cho các điểm A, B, C, D như Hình 9.24. Biết rằng $\widehat {ABC} = \widehat {A{\rm{D}}B}$ . Hãy chứng minh ΔABC ∽ ΔADB và $A{B^2} = A{\rm{D}}.AC$

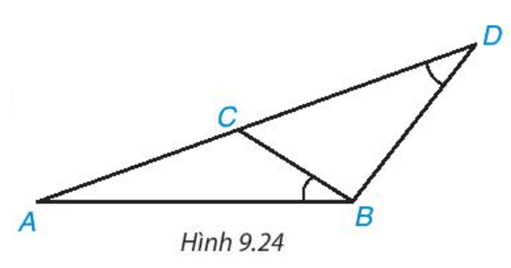
Hướng dẫn giải

Xét tam giác ABC và tam giác ADB có

$\widehat {ABC} = \widehat {A{\rm{D}}B}$ và $\widehat A$ chung

=> ΔABC ∽ ΔADB (g.g)

=> $\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}$

=> $A{B^2} = A{\rm{D}}.AC$

Thử thách nhỏ trang 90 Toán 8 Tập 2:

1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu $\widehat {A'I'B'} = \widehat {AIB}$ và $\widehat {A'I'C'} = \widehat {AIC}$ thì $\Delta A'B'C' \backsim \Delta ABC$ .

2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?

Hướng dẫn giải

1. Do tổng các góc trong một tam giác bằng $180^{\circ}$ nên:

$\frac{\widehat{A^{\prime}}+\widehat{B^{\prime}}}{2}=180^{\circ}-\widehat{A^{\prime} I^{\prime} B^{\prime}}=180^{\circ}-\widehat{A I B}=\frac{\widehat{A}+\widehat{B}}{2} \text {. }$

Suy ra $\widehat{A^{\prime}}+\widehat{B^{\prime}}=\widehat{A}+\widehat{B}$ . Do đó $\widehat{C^{\prime}}=180^{\circ}-\widehat{A^{\prime}}-\widehat{B^{\prime}}=180^{\circ}-\widehat{A}-\widehat{B}=\widehat{C} \text {. }$

Tương tự, $\widehat{B^{\prime}}=\widehat{B}$ . Vậy $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B C$ có: $\widehat{B^{\prime}}=\widehat{B}, \widehat{C^{\prime}}=\widehat{C}$ . Do đó $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ (g.g).

2. Nếu góc C và C' đều nhọn: Lấy điểm trên tia sao cho $\triangle A B M \perp \triangle A^{\prime} B^{\prime} C^{\prime}$ . Giả sử điểm không trùng với . Khi đó: $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B M$ nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}$ và kéo theo , hay $\triangle A M C$ cân tại .

+) Nếu nằm giữa và thì $\widehat{A M B}=180^{\circ}-\widehat{A M C}$

$=180^{\circ}-\widehat{A C M}>90^{\circ}>\widehat{A^{\prime} C^{\prime} M^{\prime}}$ và ta nhận được điều vô lí.

+) Vậy ở giữa và (như hình 9.19). Khi đó $\widehat{A C B}=180^{\circ}-\widehat{A C M}$

$=180^{\circ}-\widehat{A M B}=180^{\circ}-\widehat{C}>90^{\circ}$ và ta nhận được điều vô lí.

Vậy điểm phải trùng với và $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ .

Bài 9.5 trang 90 Toán 8 KNTT tập 2

Khẳng đinh nào sau đây chứng tỏ Ba trường hợp đồng dạng của hai tam giác?

a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia

b) Hai cạnh của tam giá này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau

c) Hai góc của tam giác này bằng hai góc của tam giác kia

d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia

Hướng dẫn giải

Khẳng định a chứng tỏ Ba trường hợp đồng dạng của hai tam giác

Bài 9.6 trang 90 Toán 8 KNTT tập 2

Cho Ba trường hợp đồng dạng của hai tam giác. Tam giác thứ nhất có độ dài ba cạnh là 4cm, 8cm và 10cm. Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6cm, 12cm, 15cm
b) 8cm, 16cm, 20cm
c) 6cm, 9cm, 18cm
d) 8cm, 10cm, 15cm

Hướng dẫn giải

Có chu vi tam giác là: a + b + c = 33cm => loại phương án b

Xét phương án a, nhận thấy $\frac{4}{6}=\frac{8}{12}=\frac{10}{15}=\frac{2}{3}$

=> phương án a là phương án đúng.

Bài 9.7 trang 90 Toán 8 KNTT tập 2

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng $\Delta A'B'C'$ ~ $\Delta ABC$

Chứng minh rằng $\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}$

Hướng dẫn giải

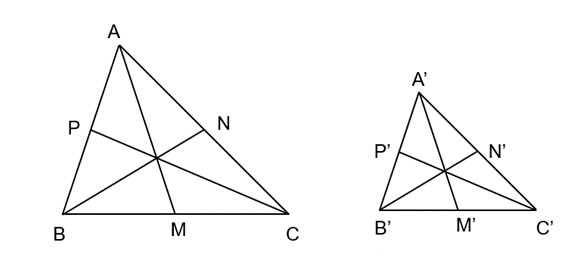
Bài 9.7

Vì $\Delta A'B'C'$ ~ $\Delta ABC$

=> $\Delta A'M'B'$ ~ $\Delta AMB$

=> $\frac{A'M'}{AM}=\frac{A'B'}{AB}$ (1)

Vì $\Delta A'B'C'$ ~ $\Delta ABC$

=> Vì $\Delta A'B'N'$ ~ $\Delta ABN$

=> $\frac{B'N'}{BN}=\frac{A'B'}{AB}$ (2)

Từ (1) và (2) => $\frac{A'M'}{AM}=\frac{B'N'}{BN}$ (3)

Vì $\Delta A'B'C'$ ~ $\Delta ABC$

=> Vì $\Delta A'C'P'$ ~ $\Delta ACP$

=> $\frac{C'P'}{CP}=\frac{A'C'}{AC}$ (4)

Vì $\Delta A'B'C'$ ~ $\Delta ABC$

=> $\Delta A'M'C'$ ~ $\Delta AMC$

=> $\frac{A'M'}{AM}=\frac{A'C'}{AC}$ (5)

Từ (4) và (5) => $\frac{C'P'}{CP}=\frac{A'M'}{AM}$ (6)

Từ (3) và (6) => $\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}$

Bài 9.8 trang 90 Toán 8 KNTT tập 2

Cho tam giác ABC có , . Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho , . Chứng minh rằng $\Delta ABC$ ~ $\Delta ANM$

Hướng dẫn giải

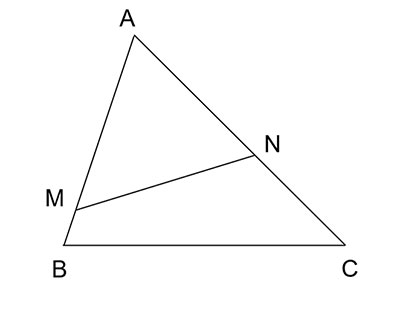
Bài 9.8

Có , => $\frac{AN}{AB}=\frac{8}{12}=\frac{2}{3}$

, => $\frac{AM}{AC}=\frac{10}{15}=\frac{2}{3}$

=> $\frac{AN}{AB}=\frac{AM}{AC}$

- Xét hai tam giác ABC và tam giác ANM, có

$\frac{AN}{AB}=\frac{AM}{AC}$ , góc A chung

=> ΔABC ~ ΔANM' (c.g.c)

Bài 9.9 trang 90 Toán 8 KNTT tập 2

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho $\widehat{ABN}=\widehat{ACM}$

a) Chứng minh rằng ΔABN ~ ΔACM

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng

Hướng dẫn giải

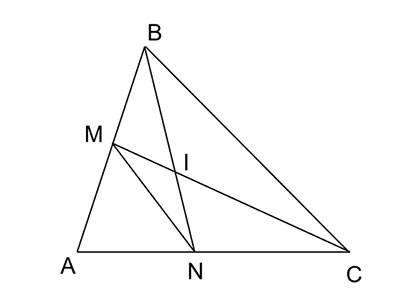
Bài 9.9

a) Xét tam giác ABN và tam giác ACM

có góc A chung, $\widehat{ABN}=\widehat{ACM}$

=> ΔABN ~ ΔACM

b) Có ΔABN ~ ΔACM

$\widehat{ANB}=\widehat{AMC}$

Có $\widehat{ANB}+\widehat{CNB}=180°$

$\widehat{AMC}+\widehat{BMC}=180°$

=> $\widehat{CNB}=\widehat{BMC}$

Xét tam giác IBM và tam giác ICN

Có $\widehat{CNB}=\widehat{BMC}$ và $\widehat{IBM}=\widehat{ICN}$

=> ΔIBM ~ ΔICN (g.g)

=> $\frac{IB}{IC}=\frac{IM}{IN}$

=>

Bài 9.10 trang 90 Toán 8 KNTT tập 2

Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất

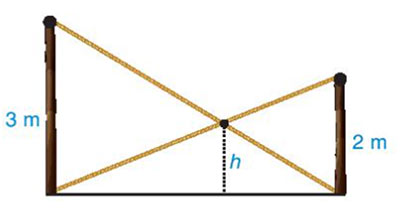
Bài 9.10

Hướng dẫn giải

Theo đề bài, ta có hình vẽ:

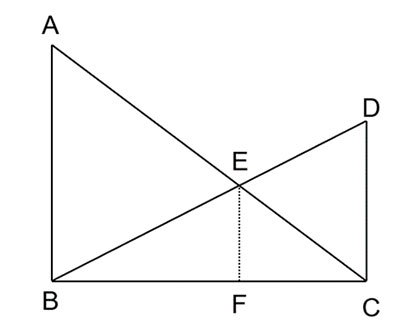
Bài 9.10

- Có AB // CD

=> $\widehat{BAC}=\widehat{DCA}$ (2 góc so le trong)

$\widehat{BDC}=\widehat{ABD}$ (2 góc so le trong)

- Xét hai tam giác ABE và tam giác CDE, có $\widehat{BAC}=\widehat{DCA}$ , $\widehat{BDC}=\widehat{ABD}$

=> ΔABE ~ ΔCDE

=> $\frac{CD}{AB}=\frac{CE}{AE}=\frac{2}{3}$

=> $\frac{CE}{AE}=\frac{2}{3}$ => $\frac{CE}{CA}=\frac{2}{5}$

- Xét hai tam giác CEF và tam giác CAB có EF // AB

=> ΔCEF ~ ΔCAB (theo định lý)

=> $\frac{FE}{AB}=\frac{CE}{CA}=\frac{2}{5}$

=> $\frac{FE}{AB}=\frac{2}{5}$ => $\frac{FE}{3}=\frac{2}{5}$ => $EF=frac{6}{5}=1,2$ (m)

Vậy độ cao h là 1,2 m

Tải về

Chọn file muốn tải về: