Giải Toán 8 trang 74 tập 1 Kết nối tri thức
Giải Toán 8 trang 74 Tập 1
Giải Toán 8 trang 74 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 74.
Bài 3.39 trang 74 Toán 8 tập 1 Kết nối
Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì còn lại là góc tù
C. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn
D. Không có tứ giác nào có ba góc tù.
Hướng dẫn giải:
Đáp án đúng: B
A. Sai vì hình chữ nhật, hình vuông không có góc tù
C. Sai vì tồn tại tứ giác có 2 góc tù, 1 góc vuông, 1 góc nhọn
D. Sai vì một tứ giác có thể có ba góc tù và một góc tù
Bài 3.40 trang 74 Toán 8 tập 1 Kết nối
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành
c) Tứ giác có ba góc vuông là hình chữ nhật
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Hướng dẫn giải:
Khẳng định sai là: a), b), d)
Khẳng định đúng: c)
Bài 3.41 trang 74 Toán 8 tập 1 Kết nối
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành
Hướng dẫn giải:
Khẳng định đúng: a), b), c)
Khẳng định sai: d) vì tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau có thể là hình thang cân
Bài 3.42 trang 74 Toán 8 tập 1 Kết nối
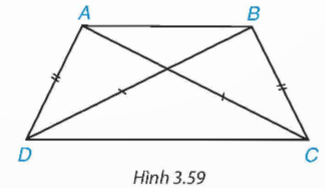
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H. 3.59)
Hướng dẫn giải:
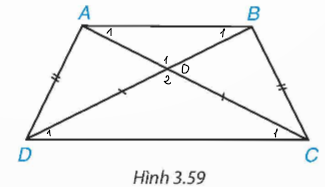
Gọi O là giao điểm của AC và BD và AD = BC
Xét tam giác ABD và tam giác BAC có:
AB chung
AD = BC (gt)
AC = BD (gt)
Do đó ∆ ABD = ∆ BAC (c . c . c)
⇒ 
\(\widehat{B_1} =\widehat{A_1}\) (hai góc tương ứng) hay ∆ OAB cân tại O
Xét tam giác ADC và tam giác BCD có:
AD chung
AD = BC (gt)
AC = BD (gt)
Do đó ∆ ADC = ∆ BCD (c . c . c)
⇒ \(\widehat{C_1} =\widehat{D_1}\) (hai góc tương ứng) hay ∆ OCD cân tại O
Xét tam giác cân OAB có: \(\widehat{A_1} =\widehat{B_1} =\frac{180^{\circ} -\widehat{O_1}}{2}\)
Xét tam giác cân ODC có \(\widehat{C_1} =\widehat{D_1} =\frac{180^{\circ} -\widehat{O_2}}{2}\)
Lại có \(\widehat{O_1} =\widehat{O_2}\) (hai góc đối đỉnh)
⇒ \(\widehat{A_1} =\widehat{C_1}\)
Mà hai góc này ở vị trí so le trong ⇒ AB // DC.
Xét tứ giác ABCD có AB // DC và AC = BD nên ABCD là hình thang cân.
Bài 3.43 trang 74 Toán 8 tập 1 Kết nối
Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
Hướng dẫn giải:
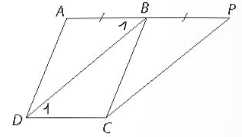
a) Vì ABCD là hình bình hành nên AB // DC và AB = DC
Xét tứ giác BPCD có BP // DC và BP = DC (= AB)
⇒ BPCD là hình bình hành (dhnb).
b) Ta có tam giác ABD vuông cân tại A nên \(\widehat{B_1} =45^{\circ}\)
Do AB // DC nên \(\widehat{B_1} =\widehat{D_1}=45^{\circ}\) (hai góc so le trong)
Vì BPCD là hình hành hành nên \(\widehat{P} =\widehat{D_1}=45^{\circ}\) (tính chất hbh)
Suy ra \(\widehat{DBP} =\widehat{DCP}=180^{\circ}- 45^{\circ} =135^{\circ}\)(tính chất hbh)
-----------------------------------------------
Lời giải Toán 8 trang 74 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài tập cuối chương 3, được VnDoc biên soạn và đăng tải!
