Giải Toán 8 trang 44 tập 1 Kết nối tri thức
Giải Toán 8 trang 44 Tập 1
Giải Toán 8 trang 44 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 44.
Luyện tập 3 trang 44 Toán 8 tập 1 Kết nối
Phân tích đa thức 2x2 – 4xy + 2y – x thành nhân tử.
Hướng dẫn giải:
Ta có: 2x2 – 4xy + 2y – x
= 2x . x – 2x . 2y – x + 2y
= 2x(x – 2y) – (x – 2y)
= (x – 2y)(2x – 1)
Vận dụng 2 trang 44 Toán 8 tập 1 Kết nối
Tính nhanh giá trị của biểu thức
A = x2 + 2y – 2x – xy tại x = 2022, y = 2020.
Hướng dẫn giải:
Ta có: A = x2 + 2y – 2x – xy
= (x2 – 2x) – (xy – 2y)
= x(x – 2) – y(x – 2)
= (x – 2)(x – y)
Thay x = 2022, y = 2020 ta có giá trị của biểu thức A là:
A = (2022 – 2)(2022 – 2020) = 2020 . 2 = 4040
Vậy giá trị của biểu thức A bằng 4040 tại x = 2022, y = 2020.
Bài 2.22 trang 44 Toán 8 tập 1 Kết nối
Phân tích các đa thức sau thành nhân tử:
a) x2 + xy
b) 6a2b – 18ab
c) x3 – 4x
d) x4 – 8x
Hướng dẫn giải:
a) x2 + xy = x . x + x . y
= x(x + y)
b) 6a2b – 18ab = 6ab . a – 6ab . 3
= 6ab(a – 3)
c) x3 – 4x = x . x2 – x . 4
= x(x2 – 4)
= x(x – 2)(x + 2)
d) x4 – 8x = x . x3 – x . 8
= x(x3 – 8)
= x(x3 – 23)
= x(x – 2)(x2 + 2x + 4)
Bài 2.23 trang 44 Toán 8 tập 1 Kết nối
Phân tích các đa thức sau thành nhân tử
a) x2 – 9 + xy + 3y
b) x2y + x2 + xy – 1
Hướng dẫn giải:
a) x2 – 9 + xy + 3y = (x2 – 9) + (xy + 3y)
= (x – 3)(x + 3) + y(x + 3)
= (x + 3)(x – 3 + y)
b) x2y + x2 + xy – 1 = (x2y + xy) + (x2 – 1)
= xy(x + 1) + (x – 1)(x + 1)
= (x + 1)(xy + x – 1)
Bài 2.24 trang 44 Toán 8 tập 1 Kết nối
Tìm x, biết:
a) x2 – 4x = 0
b) 2x3 – 2x = 0
Hướng dẫn giải:
a) x2 – 4x = 0
⇒ x(x – 4) = 0
⇒ x = 0 hoặc x – 4 = 0
⇒ x = 0 hoặc x = 4
b) 2x3 – 2x = 0
⇒ 2x(x2 – 1) = 0
⇒ 2x(x – 1)(x + 1) = 0
⇒ 2x = 0 hoặc x – 1 = 0 hoặc x + 1 = 0
⇒ x = 0 hoặc x = 1 hoặc x = – 1
Bài 2.25 trang 44 Toán 8 tập 1 Kết nối
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)
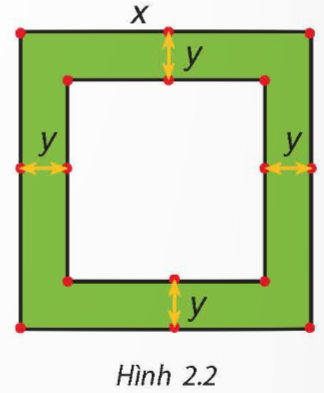
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y
b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 2 m.
Hướng dẫn giải:
a) Diện tích mảnh vườn có độ dài cạnh bằng x là: x2 (m2)
Diện tích mảnh vườn có độ dài cạnh bằng y là: y2 (m2)
Biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y là: x2 – y2 (m2)
b) Ta có: S = x2 – y2
= (x – y)(x + y)
Thay x = 102 m, y = 2 m vào S ta có:
S = (102 – 2)(102 + 2) = 100 . 104 = 10 400 (m2)
Vậy S = 10 400 m2 khi x = 102 m, y = 2 m.
-----------------------------------------------
Lời giải Toán 8 trang 44 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức bài 9: Phân tích đa thức thành nhân tử, được VnDoc biên soạn và đăng tải!








