Toán 8 Kết nối tri thức bài: Luyện tập chung trang 87
Để củng cố vững chắc kiến thức và rèn luyện kĩ năng giải bài tập, bài viết này cung cấp hướng dẫn giải chi tiết các bài tập trong mục Luyện tập chung (trang 87 và 88) thuộc Sách giáo khoa Toán 8, bộ Kết nối tri thức với cuộc sống. Nội dung bao gồm lời giải đầy đủ, rõ ràng, phân tích phương pháp áp dụng và gợi ý cách trình bày bài giải khoa học. Tài liệu này là công cụ tự học hiệu quả, giúp các em làm chủ kiến thức đã học, tự tin giải quyết mọi vấn đề và chuẩn bị tốt nhất cho các bài kiểm tra sắp tới. Mời các em cùng tham khảo chi tiết!
Toán 8 Luyện tập chung trang 88
Bài tập 4.13 trang 88 sgk Toán 8 tập 1
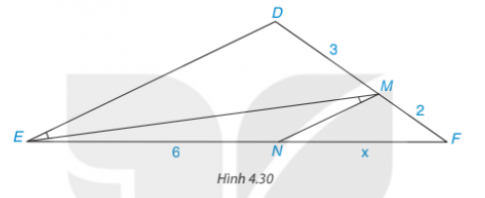
Tìm độ dài x trong Hình 4.30
Hướng dẫn giải:
Ta có: 
\(\widehat{NME}=\widehat{MED}\), hai góc ở vị trí so le trong suy ra MN//DE
\(\Rightarrow \frac{FN}{NE}=\frac{FM}{MD}\)
\(\Rightarrow \frac{x}{6}=\frac{2}{3}\Rightarrow x=4\)
Bài tập 4.14 trang 88 sgk Toán 8 tập 1
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC
a) Chứng minh EF // CD, FK // AB
b) So sánh EF và \(\frac{1}{2}(AB+CD)\)
Hướng dẫn giải:
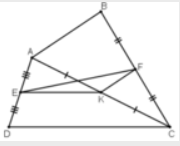
a) Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
Do đó: EK là đường trung bình của ΔADC
Suy ra: EK//DC
Xét ΔABC có
K là trung điểm của AC
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔABC
Suy ra: KF//AB
b) EK là đường trung bình của ΔADC suy ra \(EK=\frac{CD}{2}\)
KF là đường trung bình của ΔABC suy ra \(KF=\frac{AB}{2}\)
Ta có: \(EF\leq EK+KF=\frac{CD}{2}+\frac{AB}{2}=\frac{AB+CD}{2}\)
Bài tập 4.15 trang 88 sgk Toán 8 tập 1
Cho tam giác ABC, phân giác AD (\(D\in BC\)). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng \(\frac{AC}{AB}=\frac{EC}{EA}\)
Hướng dẫn giải:
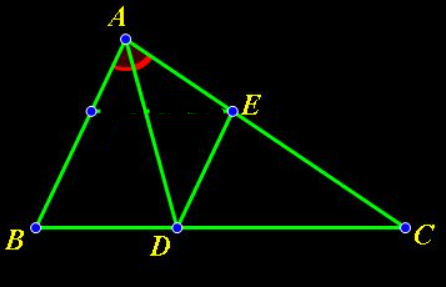
Xét tam giác ABC có AD là phân giác góc A suy ra \(\frac{AC}{AB}=\frac{CD}{DB}\) (1)
ED // AB suy ra \(\frac{EC}{EA}=\frac{CD}{DB}\) (2)
Từ (1) và (2) \(\Rightarrow \frac{AC}{AB}=\frac{EC}{EA}\)
Bài tập 4.16 trang 88 sgk Toán 8 tập 1
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D
a) Tính độ dài đoạn thẳng DB và DC
b) Tính tỉ số diện tích của hai tam giác ABD và ACD
Hướng dẫn giải:
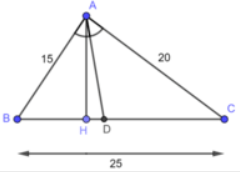
a) Trong tam giác ABC, ta có: AD là đường phân giác góc A
\(\Rightarrow \frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15 cm và AC = 20 cm (gt)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow \frac{DB}{DB+DC}=\frac{15}{15+20}\) (tính chất tỉ lệ thức)
\(\Rightarrow \frac{DB}{BC}=\frac{15}{35}\)
\(\Rightarrow DB=\frac{15}{35}\times BC=\frac{15}{35}\times 25=\frac{75}{7}\) (cm)
b) Kẻ \(AH\perp BC\)
Ta có \(S_{ABD}=\frac{1}{2}AH\times BD\)
\(S _{ACD}=\frac{1}{2}AH\times CD\)
\(\Rightarrow \frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH\times BD}{\frac{1}{2}AH\times CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow \frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}$\)
Bài tập 4.17 trang 88 sgk Toán 8 tập 1
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: \(DM^{2}=MN\times MK\)
Hướng dẫn giải:
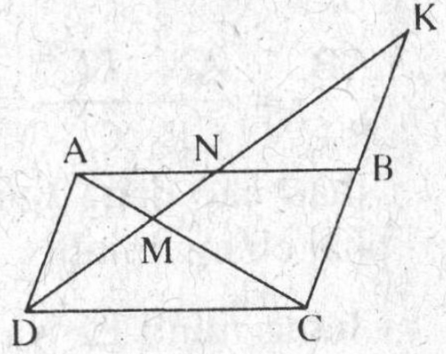
a) AD // BC (ABCD là hình bình hành) \(\Rightarrow \frac{DM}{MK}=\frac{MA}{MC}\)
AB // CD \(\Rightarrow \frac{MA}{MC}=\frac{MN}{DM}\)
Suy ra \(\frac{DM}{MK}=\frac{MN}{DM}\) hay \(DM^{2}=MN\times MK\)
