Toán 8 Bài 1 Phương trình bậc nhất một ẩn Chân trời sáng tạo

Giải Toán 8 CTST

Giải Toán 8 Chân trời sáng tạo Bài 1: Phương trình bậc nhất một ẩn tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

Giải Toán 8 CTST Bài 1: Phương trình bậc nhất một ẩn

1. Phương trình một ẩn
- Thực hành 1 trang 32 Toán 8 Tập 2:
- Vận dụng 1 trang 32 Toán 8 Tập 2:
2. Phương trình bậc nhất một ẩn và cách giải
- Khám phá 2 trang 32 Toán 8 Tập 2:
- Vận dụng 2 trang 35 Toán 8 Tập 2:
3. Giải bài tập trang 35 Toán 8 tập 2

1. Phương trình một ẩn

Thực hành 1 trang 32 Toán 8 Tập 2:

Cho phương trình 4t – 3 = 12 – t. Trong hai số 3 và 5, có số nào là nghiệm của phương trình đã cho không?

Lời giải:

• Khi t = 3, ta có 4.3 – 3 = 12 – 3 = 9.

Do đó t = 3 là nghiệm của phương trình đã cho.

• Khi t = 5, ta có 4.5 − 3 = 17 ≠ 12 − 5 = 7.

Do đó t = 5 không là nghiệm của phương trình đã cho.

Vận dụng 1 trang 32 Toán 8 Tập 2:

Đặt lên hai đĩa những quả cân như Hình 1.

a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.

b) Nếu x = 100 thì cân có thăng bằng không? Vì sao?

Nếu x = 150 thì cân có thăng bằng không? Vì sao?

Từ đó, chỉ ra một nghiệm của phương trình ở câu a.

Lời giải:

a) Do cân thăng bằng nên tổng khối lượng các vật trên hai đĩa cân bằng nhau.

Khi đó ta viết phương trình biểu thị sự thăng bằng này như sau:

3x + 100 = 400 + x.

b) Nếu x = 100, ta có 3x + 100 = 400 ≠ 400 + x = 500 nên cân không thăng bằng.

Nếu x = 150, ta có 3.150 + 100 = 400 + 150 (= 550) nên cân thăng bằng.

Vậy x = 150 là nghiệm của phương trình trên.

2. Phương trình bậc nhất một ẩn và cách giải

Khám phá 2 trang 32 Toán 8 Tập 2:

Xét cân thăng bằng ở Hoạt động khởi động.

a) Giải thích tại sao nếu ra khỏi đĩa cân một quả cân Khám phá 2 trang 32 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8 thì cân vẫn thăng bằng.

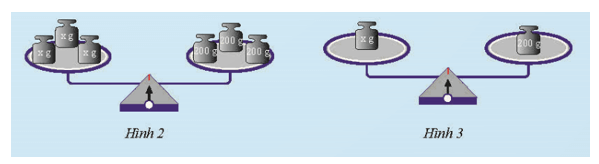
b) Nếu thay quả cân Khám phá 2 trang 32 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8 bằng ba quả cân (Hình 2) thì cân còn cân bằng không? Tại sao?

c) Tiếp theo, chia các quả cân trên mỗi đĩa cân thành ba phần bằng nhau, rồi bỏ đi hai phần (Hình 3). Khi đó, cân còn cân bằng không? Tại sao?

Lời giải:

Từ H oạt động khởi động ta có phương trình: 4x = 600 + x.

a) Bỏ ra khỏi mỗi đĩa một quả cân xg, phương trình được biến đổi như sau:

4x − x = 600 + x − x hay 3x = 600.

Vì ở cả hai vế đều bị bớt đi một lượng giống nhau nên giá trị ở cả hai đĩa cân vẫn bằng nhau và cân vẫn thăng bằng.

b) Vì quả cân 600 g gấp 3 lần quả cân 200 g nên nếu thay quả cân 600 g bằng ba quả cân 200 g thì cân vẫn cân bằng.

c) Từ hoạt động khám phá 1 ta được x = 200 là nghiệm của phương trình.

Khi chia các quả cân trên mỗi đĩa cân thành ba phần bằng nhau, rồi bỏ đi hai phần ta được khối lượng các vật còn lại trên hai đĩa là:

• Đĩa bên trái: 3x : 3 = x

• Đĩa bên phải: 600 : 3 = 200

Mà x = 200 nên cân vẫn thăng bằng.

Vận dụng 2 trang 35 Toán 8 Tập 2:

Hai bạn An và Mai giải phương trình x = 2x như sau:

An: x = 2x

1 = 2 (chia hai vế cho x)

Vậy phương trình vô nghiệm.

Mai: x = 2x

x – 2x = 0 (chuyển 2x sang vế trái)

−x = 0 (rút gọn)

x = 0 (nhân hai vế với −1)

Vậy phương trình có nghiệm x = 0.

Em hãy cho biết bạn nào giải đúng.

Lời giải:

Bạn Mai giải đúng.

Vì chỉ có thể chia hai vế cho x khi biết trước x ≠ 0.

3. Giải bài tập trang 35 Toán 8 tập 2

Bài 1 trang 35 Toán 8 Tập 2:

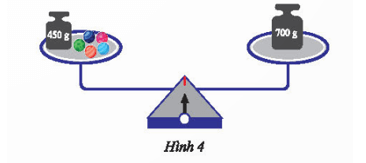
Trong Hình 4, cho biết các viên bi có cùng khối lượng là x (g) và cân thăng bằng.

Viết phương trình biểu diễn liên hệ giữa khối lượng các vật ở trên hai đĩa cân.

Bài 1 trang 35 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Các viên bi có cùng khối lượng là x (g). Khi đó:

• Khối lượng các vật ở đĩa cân bên trái là: 450 + 5x (g)

• Khối lượng của vật ở đĩa cân bên phải là: 700 (g)

Vì cân thăng bằng nên ta có phương trình:

450 + 5x = 700.

Vậy phương trình biểu diễn liên hệ giữa khối lượng các vật ở trên hai đĩa cân là 450 + 5x = 700.

Bài 2 trang 36 Toán 8 tập 2

Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số $a$ và $b$ của phương trình bậc nhất một ẩn đó.

a) $7x + \dfrac{4}{7} = 0$ $7x + \dfrac{4}{7} = 0$;

b) $\dfrac{3}{2}y - 5 = 4$ $\dfrac{3}{2}y - 5 = 4$;

c) $0t + 6 = 0$;

d) ${x^2} + 3 = 0$ ${x^2} + 3 = 0$.

Lời giải chi tiết

a) Phương trình $7x + \dfrac{4}{7} = 0$ $7x + \dfrac{4}{7} = 0$ là phương trình bậc nhất một ẩn vì có dạng $ax + b = 0$ với $a$ và $b$ là các hệ số đã cho và $a \ne 0$ $a \ne 0$, $x$ là ẩn số.

Khi đó, $a = 7;b = \dfrac{4}{7}$ $a = 7;b = \dfrac{4}{7}$.

b) $\dfrac{3}{2}y - 5 = 4$ $\dfrac{3}{2}y - 5 = 4$

$\dfrac{3}{2}y - 5 - 4 = 0$ $\dfrac{3}{2}y - 5 - 4 = 0$

$\dfrac{3}{2}y - 9 = 0$ $\dfrac{3}{2}y - 9 = 0$

Phương trình $\dfrac{3}{2}y - 9 = 0$ $\dfrac{3}{2}y - 9 = 0$ là phương trình bậc nhất một ẩn vì có dạng $ay + b = 0$ với $a$ và $b$ là các hệ số đã cho và $a \ne 0$ $a \ne 0$, $y$ là ẩn số.

Khi đó, $a = \dfrac{3}{2};b = - 9$ $a = \dfrac{3}{2};b = - 9$

c) Phương trình $0t + 6 = 0$ không là phương trình bậc nhất một ẩn.

Mặc dù phương trình đã cho có dạng $at + b = 0$ với $a$ và $b$ là các hệ số đã cho nhưng $a = 0$.

d) Phương trình ${x^2} + 3 = 0$ ${x^2} + 3 = 0$ không là phương trình bậc nhất một ẩn vì không có dạng $ax + b = 0$ với $a$ và $b$ là các hệ số đã cho và $a \ne 0$ $a \ne 0$, $x$ là ẩn số (do có ${x^2}$ ${x^2}$).

Bài 4 trang 36 Toán 8 Tập 2:

Giải các phương trình sau:

a) 8 – (x – 15) = 2(3 – 2x);

b) –6(1,5 – 2u) = 3(–15 + 2u);

c) (x + 3)² − x(x + 4) = 13;

d) (y + 5)(y − 5) − (y − 2)² = −5.

Lời giải chi tiết

8 - x + 15 = 6 - 4x

- x + 4x = 6 - 8 - 15

3x = - 17

$x = \left( { - 17} \right):3$ $x = \left( { - 17} \right):3$

$x = \dfrac{{ - 17}}{3}$ $x = \dfrac{{ - 17}}{3}$

Vậy nghiệm của phương trình là $x = \dfrac{{ - 17}}{3}$ $x = \dfrac{{ - 17}}{3}$.

b) $- 6\left( {1,5 - 2u} \right) = 3\left( { - 15 + 2u} \right)$ $- 6\left( {1,5 - 2u} \right) = 3\left( { - 15 + 2u} \right)$

- 9 + 12u = - 45 + 6u

12u - 6u = - 45 + 9

$u = \left( { - 36} \right):6$ $u = \left( { - 36} \right):6$

6u = - 36

u = - 6

Vậy nghiệm của phương trình là u = - 6.

c) ${\left( {x + 3} \right)^2} - x\left( {x + 4} \right) = 13$ ${\left( {x + 3} \right)^2} - x\left( {x + 4} \right) = 13$

$\left( {{x^2} + 6x + 9} \right) - \left( {{x^2} + 4x} \right) = 13$ $\left( {{x^2} + 6x + 9} \right) - \left( {{x^2} + 4x} \right) = 13$

${x^2} + 6x + 9 - {x^2} - 4x = 13$ ${x^2} + 6x + 9 - {x^2} - 4x = 13$

$\left( {{x^2} - {x^2}} \right) + \left( {6x - 4x} \right) = 13 - 9$ $\left( {{x^2} - {x^2}} \right) + \left( {6x - 4x} \right) = 13 - 9$

2x = 4

x = 4:2

x = 2

Vậy nghiệm của phương trình là x = 2.

d) $\left( {y + 5} \right)\left( {y - 5} \right) - {\left( {y - 2} \right)^2} = -5$ $\left( {y + 5} \right)\left( {y - 5} \right) - {\left( {y - 2} \right)^2} = -5$

$\left( {{y^2} - 25} \right) - \left( {{y^2} - 4y + 4} \right) = -5$ $\left( {{y^2} - 25} \right) - \left( {{y^2} - 4y + 4} \right) = -5$

${y^2} - 25 - {y^2} + 4y - 4 = -5$ ${y^2} - 25 - {y^2} + 4y - 4 = -5$

$\left( {{y^2} - {y^2}} \right) + 4y = -5 + 4 + 25$ $\left( {{y^2} - {y^2}} \right) + 4y = -5 + 4 + 25$

4y = 24

y = 24:4

y = 6

Vậy nghiệm của phương trình là y = 6.

-------------------------------------

Ngoài Giải Toán 8 Bài 1: Phương trình bậc nhất một ẩn CTST, mời các bạn tham khảo thêm Đề thi giữa kì 2 lớp 8 hay Đề thi học kì 2 lớp 8 để giúp các bạn học sinh học tốt hơn.

Bài tiếp theo:

Chia sẻ, đánh giá bài viết

1

380

Bài trước

Bài sau