Toán 8 Bài 2: Đường trung bình của tam giác

Giải Toán 8 CTST

Giải Toán 8 Chân trời sáng tạo Bài 2 Đường trung bình của tam giác tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

1. Đường trung bình của tam giác

Khám phá 1 trang 52 Toán 8 Tập 2

Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC.

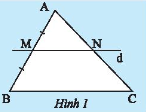
Hướng dẫn giải:

Xét tam giác ABC có MN//BC nên áp dụng định lí Thales cho tam giác ta có:

$\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}.$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}.$

Mà M là trung điểm của AB nên $AM = \frac{1}{2}BC$ $AM = \frac{1}{2}BC$ hay $\frac{{AM}}{{BC}} = \frac{1}{2}.$ $\frac{{AM}}{{BC}} = \frac{1}{2}.$

Do đó, $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow AN = \frac{1}{2}AC.$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow AN = \frac{1}{2}AC.$

Do đó, N là trung điểm của AC.

Thực hành 1 trang 52 Toán 8 Tập 2

Tìm độ dài đoạn thẳng NQ trong Hình 4.

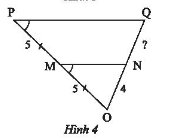
Hướng dẫn giải:

Từ hình vẽ ta có: $\widehat {OMN} = \widehat {OPQ}.$ $\widehat {OMN} = \widehat {OPQ}.$

Mà hai góc này ở vị trí đồng vị nên MN//PQ

Xét tam giác OPQ có MN//PQ nên áp dụng định lí Thales cho tam giác ta có:

$\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \Leftrightarrow \frac{5}{5} = \frac{4}{{NQ}} \Rightarrow NQ = \frac{{4.5}}{5} = 4.$ $\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \Leftrightarrow \frac{5}{5} = \frac{4}{{NQ}} \Rightarrow NQ = \frac{{4.5}}{5} = 4.$

Vậy NQ = 4.

Vận dụng 1 trang 53 Toán 8 Tập 2

Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC.

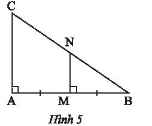
Hướng dẫn giải:

Vì $\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right. \Rightarrow MN//CA$ $\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right. \Rightarrow MN//CA$ (Quan hệ từ vuông góc đến song song).

Ta có:

$AM = BM \Rightarrow BM = \frac{1}{2}AB \Leftrightarrow \frac{{BM}}{{AB}} = \frac{1}{2}$ $AM = BM \Rightarrow BM = \frac{1}{2}AB \Leftrightarrow \frac{{BM}}{{AB}} = \frac{1}{2}$ hay M là trung điểm của AB.

Xét tam giác ABC có NM//AC; MN cắt BA; BC lần lượt tại M; N. Theo hệ quả của định lí Thales ta có:

$\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} \Leftrightarrow \frac{{BN}}{{BC}} = \frac{1}{2}$ $\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} \Leftrightarrow \frac{{BN}}{{BC}} = \frac{1}{2}$

Hay 2BN = BC. Do đó, N là trung điểm của BC.

Xét tam giác ABC có:

M là trrung điểm của AB

N là trrung điểm của BC

Do đó, MN là đường trung bình của tam giác ABC (điều phải chứng minh).

2. Tính chất của đường trung bình

Khám phá 2 trang 53 Toán 8 Tập 2

Cho $M,N$ lần lượt là trung điểm của hai cạnh $AB;AC$ của tam giác $ABC$.

a) Tính các tỉ số $\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}$ $\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}$;

b) Cứng mình $MN//BC$;

c) Chứng minh $\frac{{MN}}{{BC}} = \frac{1}{2}$ $\frac{{MN}}{{BC}} = \frac{1}{2}$.

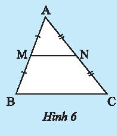
Hướng dẫn giải:

a) Vì $AM = MB \Rightarrow M$ $AM = MB \Rightarrow M$ là trung điểm của $AB$ (do $M$ thuộc $AB$)

$\Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}$ $\Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}$;

Vì $AN = NC \Rightarrow N$ $AN = NC \Rightarrow N$ là trung điểm của $AC$ (do $N$ thuộc $AC$)

$\Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}$ $\Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}$.

b) Vì $\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ $\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$.

Xét tam giác $ABC$ có $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ nên áp dụng định lí Thales đảo ta được $MN//BC$.

c) Xét tam giác $ABC$ có $MN//BC$ nên áp dụng hệ quả định lí Thales ta được $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}$

Mà $\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}$ $\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}$.

Vậy $\frac{{MN}}{{BC}} = \frac{1}{2}$ $\frac{{MN}}{{BC}} = \frac{1}{2}$ (điều phải chứng minh).

Thực hành 2 trang 53 Toán 8 Tập 2

Trong Hình 8, cho biết $JK = 10cm;DE = 6,5cm;EL = 3,7cm$. Tính $DJ;EF;DF;KI$.

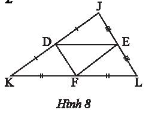
Hướng dẫn giải:

Vì $DJ = KD \Rightarrow D$ $DJ = KD \Rightarrow D$ là trung điểm của $JK$

$\Rightarrow DJ = DK = \frac{1}{2}JK = \frac{1}{2}.10 = 5cm$ $\Rightarrow DJ = DK = \frac{1}{2}JK = \frac{1}{2}.10 = 5cm$;

Vì $EJ = EL \Rightarrow E$ $EJ = EL \Rightarrow E$ là trung điểm của $JL$.

$\Rightarrow 2EL = JL \Leftrightarrow JL = 2.3,7 = 7,4cm$ $\Rightarrow 2EL = JL \Leftrightarrow JL = 2.3,7 = 7,4cm$.

Vì $KF = LF \Rightarrow F$ $KF = LF \Rightarrow F$ là trung điểm của $KL$.

- Vì $D$ là trung điểm của $JK$; $E$ là trung điểm của $JL$ nên $ED$ là đường trung bình của tam giác $JLK$ $\Rightarrow ED = \frac{1}{2}KL$ $\Rightarrow ED = \frac{1}{2}KL$ (tính chất đường trung bình)

Do đó, $KL = 2ED = 2.6,5 = 13cm$;

- Vì $E$ là trung điểm của $JL$; $F$ là trung điểm của $KL$ nên $EF$ là đường rung bình của tam giác $JLK$ $\Rightarrow EF = \frac{1}{2}JK$ $\Rightarrow EF = \frac{1}{2}JK$ (tính chất đường trung bình)

$\Leftrightarrow EF = \frac{1}{2}.10 = 5cm$ $\Leftrightarrow EF = \frac{1}{2}.10 = 5cm$.

- Vì $D$ là trung điểm của $KJ$; $F$ là trung điểm của $KL$ nên $DF$ là đường rung bình của tam giác $JLK$ $\Rightarrow DF = \frac{1}{2}JL$ $\Rightarrow DF = \frac{1}{2}JL$ (tính chất đường trung bình)

$\Leftrightarrow DF = \frac{1}{2}.7,4 = 3,7cm$ $\Leftrightarrow DF = \frac{1}{2}.7,4 = 3,7cm$.

Vậy $DJ = 5cm;EF = 5cm;DF = 3,7cm;KL = 13cm$

Vận dụng 2 trang 53 Toán 8 Tập 2

Hãy tính khoảng cách $BC$ trong phần câu hỏi khởi động trang 52.

Hướng dẫn giải:

Vì $BD = DA \Rightarrow D$ $BD = DA \Rightarrow D$ là trung điểm của $AB$;

Vì $EC = EA \Rightarrow E$ $EC = EA \Rightarrow E$ là trung điểm của $AC$.

Do đó, $DE$ là đường trung bình của tam giác $ABC$

$\Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.$ (tính chất đường trung bình).

$\Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)$ $\Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)$

Vậy khoảng các của hai điểm $B$ và $C$ là 90 m.

Bài tập

Bài 1 trang 53 Toán 8 Tập 2:

Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình.

Hướng dẫn giải

a) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

x = 12.

b) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

2x + 3 = 14

x = 112.

c) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

58 = 2(5x − 1)

58 = 10x – 2

x = 6

Bài 2 trang 54 Toán 8 Tập 2:

Tính độ dài đoạn PQ (Hình 10).

Hướng dẫn giải

Xét tam giác ABC có:

AP = PB = 8 cm

AQ = QC = 7 cm

Khi đó, PQ là đường trung bình tam giác ABC.

Do đó PQ = $\frac{1}{2}$ $\frac{1}{2}$BC = $\frac{1}{2}$ $\frac{1}{2}$.9 = 4,5 (cm).

Bài 5 trang 54 Toán 8 Tập 2:

Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Hướng dẫn giải

Xét tam giác ABC ta có:

M là trung điểm của AB (gt);

N là trung điểm của AC (gt);

Do đó MN là đường trung bình của tam giác ABC nên MN // BC.

Suy ra tứ giác MNPH là hình thang.

Xét tam giác ABC ta có:

M là trung điểm của AB (gt);

P là trung điểm của BC;

Do đó MP là đường trung bình của tam giác ABC nên MN= $\frac{1}{2}$ $\frac{1}{2}$AC

Vì ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC) nên NH= $\frac{1}{2}$ $\frac{1}{2}$AC

Mà MP= $\frac{1}{2}$ $\frac{1}{2}$AC (cmt) nên NH = MP.

Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.

Bài 6 trang 54 Toán 8 Tập 2:

Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.

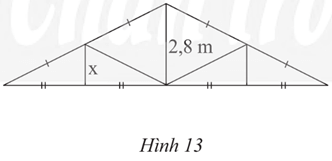
Bài 6 trang 54 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Hướng dẫn giải

Xét tam giác ABH có:

AD = BD

BE = EH

Do đó DE là đường trung bình tam giác ABH nên DE= $\frac{1}{2}$ $\frac{1}{2}$AH

Khi đó x= $\frac{1}{2}$ $\frac{1}{2}$.2,8=1,4(m)

Bài 7 trang 54 Toán 8 Tập 2:

Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE.

Hướng dẫn giải

Xét tam giác ADE có:

B là trung điểm AD

C là trung điểm AE

Do đó BC là đường trung bình của tam giác ADE.

Khi đó DE = 2BC = 2.232 = 464 (m).

Chia sẻ, đánh giá bài viết

1

207

Bài trước

Bài sau