VnDoc.com

Toán 8 Chân trời sáng tạo Bài 1: Hai tam giác đồng dạng

Giải Toán 8 CTST

Bài trước

Tải về

Bài sau

Giải Toán 8 Chân trời sáng tạo Bài 1: Hai tam giác đồng dạng tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

Giải Toán 8 CTST Bài 1: Hai tam giác đồng dạng

Bài 1 trang 65 Toán 8 Tập 2:
Bài 2 trang 65 Toán 8 Tập 2:
Bài 3 trang 65 Toán 8 Tập 2:
Bài 4 trang 65 Toán 8 Tập 2:
Bài 5 trang 65 Toán 8 Tập 2:
Bài 6 trang 65 Toán 8 Tập 2:

Bài 1 trang 65 Toán 8 Tập 2:

Trong hai khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác đồng dạng với nhau thì bằng nhau.

Hướng dẫn giải

a) Xét khẳng định a: Hai tam giác bằng nhau thì đồng dạng với nhau.

Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1.

Vậy khẳng định a đúng.

b) Xét khẳng định b: Hai tam giác đồng dạng với nhau thì bằng nhau.

Hai tam giác đồng dạng có các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỷ lệ với nhau theo tỉ số k.

• Với k = 1 thì các cạnh tương ứng của hai tam giác đó bằng nhau nên hai tam giác đó bằng nhau.

• Với k ≠ 1 thì các cạnh tương ứng của hai tam giác đó không bằng nhau nên hai tam giác đó không bằng nhau.

Vậy khẳng định b sai.

Bài 2 trang 65 Toán 8 Tập 2:

Cho tam giác ABC, hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k= $\frac{1}{2}$ $\frac{1}{2}$

Hướng dẫn giải

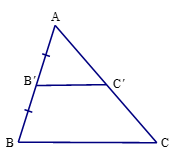
Trên cạnh AB lấy B' là trung điểm của AB

Qua B' kẻ đường thẳng song song với BC cắt AC tại C'

Ta có: B'C' // BC nên ΔAB′C′ ᔕ ΔABC theo tỉ số đồng dạng k= $\frac{AB$ $\frac{A B^{'}}{A}$ = $\frac{1}{2}$ $\frac{1}{2}$

Bài 3 trang 65 Toán 8 Tập 2:

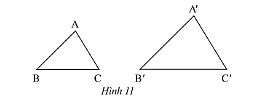
a) Trong Hình 11, cho biết $\Delta ABC\backsim\Delta A$ $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ . Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

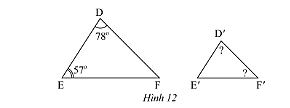
b) Trong Hình 12, cho biết $\Delta DEF\backsim\Delta D$ $Δ D E F ∽ Δ D^{'} E^{'} F^{'}$ . Tính số đo $\widehat {D$ $\hat{D^{'}}$ và $\widehat F$ $\hat{F}$ .

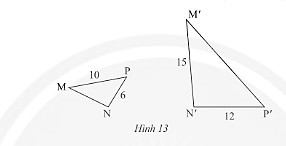
c) Trong Hình 12, cho biết $\Delta MNP\backsim\Delta M$ $Δ M N P ∽ Δ M^{'} N^{'} P^{'}$ . Tính độ dài các đoạn thẳng MN và MP'.

Hướng dẫn giải

a) Ta có: $\Delta ABC\backsim\Delta A$ $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ thì $\left\{ \begin{array}{l}\widehat A = \widehat {A$ ${\begin{cases} \hat{A} = \hat{A^{'}}; \hat{B} = \hat{B^{'}}; \hat{C} = \hat{C^{'}} \\ \frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C} = \frac{B^{'} C^{'}}{B C} = k \end{cases} .$

b) Xét tam giác DEF có:

$\widehat D + \widehat E + \widehat F = 180^\circ$ $\hat{D} + \hat{E} + \hat{F} = 180^{\circ}$ (tổng ba góc trong một tam giác).

Ta có: $\widehat D = 78^\circ ;\widehat E = 57^\circ$ $\hat{D} = 78^{\circ}; \hat{E} = 57^{\circ}$ thay số ta được

$78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ$ $78^{\circ} + 57^{\circ} + \hat{F} = 180^{\circ} \Rightarrow \hat{F} = 180^{\circ} - 78^{\circ} - 57^{\circ} = 45^{\circ}$

Ta có: $\Delta DEF\backsim\Delta D$ $Δ D E F ∽ Δ D^{'} E^{'} F^{'}$ suy ra

$\widehat D = \widehat {D$ $\hat{D} = \hat{D^{'}}; \hat{E} = \hat{E^{'}}; \hat{F} = \hat{F^{'}}$ (các góc tương ứng bằng nhau)

Do đó, $\widehat D = \widehat {D$ $\hat{D} = \hat{D^{'}} = 78^{\circ}; \hat{F} = \hat{F^{'}} = 45^{\circ} .$

c) Ta có $\Delta MNP\backsim\Delta M$ $Δ M N P ∽ Δ M^{'} N^{'} P^{'}$ suy ra

$\frac{{MN}}{{M$ $\frac{M N}{M^{'} N^{'}} = \frac{M P}{M^{'} P^{'}} = \frac{N P}{N^{'} P^{'}}$ (các cặp cạnh tương ứng có cùng tỉ lệ).

Với MP = 10;NP = 6;M'N' = 15;N'P' = 12 thay vào ta được:

$\left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M$ ${\begin{cases} \frac{M N}{15} = \frac{1}{2} \\ \frac{10}{M^{'} P^{'}} = \frac{1}{2} \end{cases} \Rightarrow {\begin{cases} M N = \frac{15.1}{2} = 7, 5 \\ M^{'} P^{'} = \frac{10.2}{1} = 20 \end{cases} .$

Vậy MN = 7,5;M'P' = 20.

Bài 4 trang 65 Toán 8 Tập 2:

Trong Hình 14, cho biết AB//CD

a) Chứng minh rằng $\Delta AEB\backsim\Delta DEC.$ $Δ A E B ∽ Δ D E C .$

b) Tìm x.

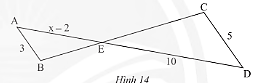
Hướng dẫn giải

a) Xét tam giác ABE có:

AB//CD và C,D cắt BE;AE lần lượt tại C,D.

Do đó, $\Delta AEB\backsim\Delta DEC$ $Δ A E B ∽ Δ D E C$ (định lí)

b) Vì $\Delta AEB\backsim\Delta DEC$ $Δ A E B ∽ Δ D E C$ nên $\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}$ $\frac{A E}{E D} = \frac{A B}{C D}$ (các cặp cạnh tương ứng có cùng tỉ lệ).

Thay số ta được:

$\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8$ $\frac{x - 2}{10} = \frac{3}{5} \Rightarrow x - 2 = \frac{10.3}{5} = 6 \Rightarrow x = 6 + 2 = 8$

Vậy x = 8.

Bài 5 trang 65 Toán 8 Tập 2:

Cho $\Delta ABC\backsim\Delta DEF$ $Δ A B C ∽ Δ D E F$ theo tỉ sống đồng dạng $k = \frac{2}{5}.$ $k = \frac{2}{5} .$

a) Tính tỉ số chu vi của hai tam giác đã cho.

b) Cho biết hiệu chu vi hai tam giác trên là 36cm, tính chu vi mỗi tam giác.

Hướng dẫn giải

a) Ta có $\Delta ABC\backsim\Delta DEF$ $Δ A B C ∽ Δ D E F$ theo tỉ số đồng dạng $k = \frac{2}{5}$ $k = \frac{2}{5}$ nên

$\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{5} \Rightarrow AB = \frac{2}{5}DE;AC = \frac{2}{5}DF;BC = \frac{2}{5}EF.$ $\frac{A B}{D E} = \frac{A C}{D F} = \frac{B C}{E F} = \frac{2}{5} \Rightarrow A B = \frac{2}{5} D E; A C = \frac{2}{5} D F; B C = \frac{2}{5} E F .$

Chu vi tam giác ABC là:

${C_{ABC}} = AB + AC + BC$ $C_{A B C} = A B + A C + B C$ (đơn vị độ dài).

Chu vi tam giác DEF là:

${C_{DEF}} = DE + DF + EF$ $C_{D E F} = D E + D F + E F$

Tỉ số chu vi của \Delta ABC và \Delta DEF là:

$\frac{{{C_{ABC}}}}{{{C_{DEF}}}} = \frac{{AB + AC + BC}}{{DE + DF + EF}} = \frac{{\frac{2}{5}DE + \frac{2}{5}DF + \frac{2}{5}EF}}{{DE + DF + EF}} = \frac{{\frac{2}{5}\left( {DE + DF + EF} \right)}}{{DE + DF + EF}} = \frac{2}{5}.$ $\frac{C_{A B C}}{C_{D E F}} = \frac{A B + A C + B C}{D E + D F + E F} = \frac{\frac{2}{5} D E + \frac{2}{5} D F + \frac{2}{5} E F}{D E + D F + E F} = \frac{\frac{2}{5} (D E + D F + E F)}{D E + D F + E F} = \frac{2}{5} .$

b) Chu vi tam giác ABC là:

$36:\left( {5 - 2} \right).2 = 24\left( {cm} \right)$ $36 : (5 - 2) .2 = 24 (c m)$

Chu vi tam giác DEF là:

$36:\left( {5 - 2} \right).5 = 60\left( {cm} \right)$ $36 : (5 - 2) .5 = 60 (c m)$

Vậy chu vi tam giác ABC là 24cm; chu vi tam giác DEF là 60cm.

Bài 6 trang 65 Toán 8 Tập 2:

Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai điểm không thể đến được (hình 15). Biết DE//BC.

a) Chứng minh rằng \Delta ADE\backsim\Delta ABC.

b) Tính khoảng cách BC.

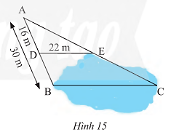
Hướng dẫn giải

a) Xét tam giác ABC ta có:

DE//BC và D,E cắt AB;AC tại D;E.

Do đó, $\Delta ADE\backsim\Delta ABC$ $Δ A D E ∽ Δ A B C$ (định lí)

b) Vì $\Delta ADE\backsim\Delta ABC$ $Δ A D E ∽ Δ A B C$ nên $\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}$ $\frac{A D}{A B} = \frac{D E}{B C}$ (cách cặp cạnh tương ứng có cùng tỉ lệ).

Thay số, $\frac{{16}}{{30}} = \frac{{22}}{{BC}} \Rightarrow BC = \frac{{22.30}}{{16}} = 41,25$ $\frac{16}{30} = \frac{22}{B C} \Rightarrow B C = \frac{22.30}{16} = 41, 25$

Vậy BC = 41,25m.

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

116

Bài trước

Bài sau

Chia sẻ bởi:
Chuột nhắt

Tải về

Chọn file muốn tải về:

Toán 8 Chân trời sáng tạo Bài 1: Hai tam giác đồng dạng

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!