Toán 8 Chân trời sáng tạo bài 3: Hình thang - Hình thang cân

Sách Chân trời sáng tạo

Giải Toán 8 Chân trời sáng tạo bài 3: Hình thang - Hình thang cân được VnDoc sưu tầm và giới thiệu với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 Chân trời sáng tạo. Mời các em cùng tham khảo để nắm được nội dung bài học.

1. Hình thang - Hình thang cân

Thực hành 1 trang 69 sgk Toán 8 tập 1 CTST: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em

a) $\widehat{Q}=90^{\circ};\widehat{N}=125^{\circ}$ $\widehat{Q}=90^{\circ};\widehat{N}=125^{\circ}$

b) $\widehat{P}=\widehat{Q}=110^{\circ}$ $\widehat{P}=\widehat{Q}=110^{\circ}$

Bài giải

a) Hình thang MNPQ (MN//PQ) có $\widehat{Q}=90$ $\widehat{Q}=90$nên là hình thang vuông. Suy ra

$\widehat{Q}=\widehat{M}=90^{\circ};\widehat{P}=180^{\circ}-\widehat{N}=180^{\circ}-125^{\circ}=55^{\circ}$ $\widehat{Q}=\widehat{M}=90^{\circ};\widehat{P}=180^{\circ}-\widehat{N}=180^{\circ}-125^{\circ}=55^{\circ}$

b) Hình thang MNPQ (MN//PQ) có $\widehat{P}=\widehat{Q}=110^{\circ}$ $\widehat{P}=\widehat{Q}=110^{\circ}$ nên là hình thang cân

Suy ra $\widehat{M}=\widehat{N}=180^{\circ}-110^{\circ}=70^{\circ}$ $\widehat{M}=\widehat{N}=180^{\circ}-110^{\circ}=70^{\circ}$

Vận dụng 1 trang 69 sgk Toán 8 tập 1 CTST: Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân ABCD. Cho biết $\widehat{D}=\widehat{C}=75^{\circ}$ $\widehat{D}=\widehat{C}=75^{\circ}$. Tìm số đo $\widehat{A};\widehat{B}$ $\widehat{A};\widehat{B}$

Bài giải

Hình thang ABCD (AB // CD) có $\widehat{D}=\widehat{C}=75^{\circ}$ $\widehat{D}=\widehat{C}=75^{\circ}$ suy ra $\widehat{A}=\widehat{B}=180^{\circ}-75^{\circ}=105^{\circ}$ $\widehat{A}=\widehat{B}=180^{\circ}-75^{\circ}=105^{\circ}$

Vận dụng 2 trang 69 sgk Toán 8 tập 1 CTST: Tứ giác EFGH có các góc cho như Hình 5

a) Chứng minh rằng EFGH là hình thang

b) Tìm góc chưa biết của tứ giác

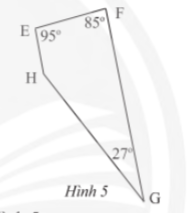
Giải Vận dụng 2 trang 69 sgk Toán 8 tập 1 Chân trời

Bài giải

a) Ta có: $\widehat{E}+\widehat{F}=95^{\circ}+85^{\circ}=180^{\circ}$ $\widehat{E}+\widehat{F}=95^{\circ}+85^{\circ}=180^{\circ}$ hay $\widehat{E};\widehat{F}$ $\widehat{E};\widehat{F}$ là hai góc bù nhau mà chúng lại ở vị trí trong cùng phía suy ra EH // FG

Do đó EFGH là hình thang

b) Hình thang EFGH (EH // FG) có:

$\widehat{H}=180^{\circ}-\widehat{G}=180^{\circ}-27^{\circ}=153^{\circ}$ $\widehat{H}=180^{\circ}-\widehat{G}=180^{\circ}-27^{\circ}=153^{\circ}$

2. Tính chất của hình thang cân

Thực hành 2 trang 70 sgk Toán 8 tập 1 CTST: Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy là MN và PQ

Bài giải

MQ = NP

MP = NQ

Vận dụng 3 trang 69 sgk Toán 8 tập 1 CTST: Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo

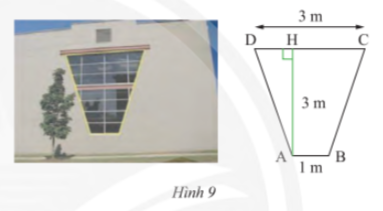
Giải Vận dụng 3 trang 69 sgk Toán 8 tập 1 Chân trời

Bài giải

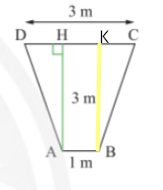
Giải Vận dụng 3 trang 69 sgk Toán 8 tập 1 Chân trời

Kẻ BK vuông góc với CD ta có: HK = AB, DH = CK = (3 - 1) : 2 = 1(m)

Áp dụng định lí Pythagore tam giác AHD vuông tại H ta có:

$AD^{2}=AH^{2}+DH^{2}=3^{2}+1^{2}=10$ $AD^{2}=AH^{2}+DH^{2}=3^{2}+1^{2}=10$. Do đó $AD=\sqrt{10}$ $AD=\sqrt{10}$ (m)

Suy ra $AD=BC=\sqrt{10}$ $AD=BC=\sqrt{10}$m

Áp dụng định lí Pythagore tam giác AHC vuông tại H ta có:

$AC^{2}=AH^{2}+CH^{2}=3^{2}+2^{2}=13$ $AC^{2}=AH^{2}+CH^{2}=3^{2}+2^{2}=13$. Do đó $AC=\sqrt{13}$ $AC=\sqrt{13}$(m)

Suy ra $AC=BD=\sqrt{13}$ $AC=BD=\sqrt{13}$m

3. Dấu hiệu nhận biết hình thang cân

Thực hành 3 trang 71 sgk Toán 8 tập 1 CTST: Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12

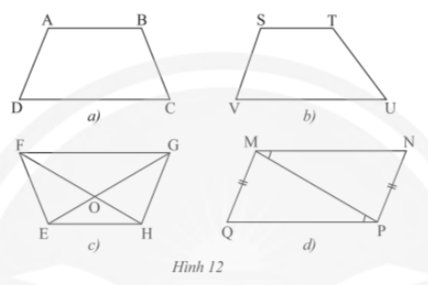
Giải Thực hành 3 trang 71 sgk Toán 8 tập 1 Chân trời

Bài giải

a) c) là hình thang cân

Vận dụng 4 trang 71 sgk Toán 8 tập 1 CTST: Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo $MN =NQ = $8\sqrt{2}$ $8\sqrt{2}$ cm. Tính độ dài đường cao và cạnh bên của hình thang.

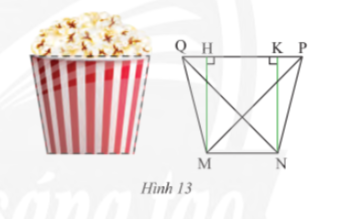
Giải Vận dụng 4 trang 71 sgk Toán 8 tập 1 Chân trời

Bài giải

Ta có QH = PK = (10 - 6) : 2 = 2(cm)

Áp dụng định lí Pythagore cho tam giác MPH vuông tại H ta có:

$MP^{2}=MH^{2}+PH^{2}\Rightarrow MH^{2}=MP^{2}-PH^{2}=128-64=64$ $MP^{2}=MH^{2}+PH^{2}\Rightarrow MH^{2}=MP^{2}-PH^{2}=128-64=64$ do đó MH = 8 cm

Áp dụng định lí Pythagore cho tam giác MHQ vuông tại H ta có:

$MQ^{2}=MH^{2}+QH^{2}=64-4=60$ $MQ^{2}=MH^{2}+QH^{2}=64-4=60$ do đó MH = $2\sqrt{15}$ $2\sqrt{15}$ cm

Vậy độ dài đường cao là 8 cm, độ dài cạnh bên là $2\sqrt{15}$ $2\sqrt{15}$ cm

4. Bài tập

Bài tập 1 trang 71 sgk Toán 8 tập 1 CTST: TÌm x và y ở các hình sau.

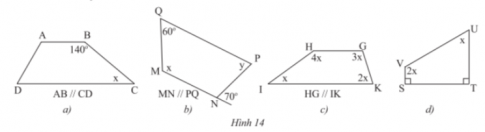
Giải Bài tập 1 trang 71 sgk Toán 8 tập 1 Chân trời

Bài giải

$a) x=180^{\circ}-140^{\circ}=40^{\circ}$ $a) x=180^{\circ}-140^{\circ}=40^{\circ}$

$b) x=180^{\circ}-60^{\circ}=120^{\circ}$ $b) x=180^{\circ}-60^{\circ}=120^{\circ}$

MN // PQ suy ra $y=\widehat{N}_{ngoài}=70^{\circ}$ $y=\widehat{N}_{ngoài}=70^{\circ}$

c) Ta có: $4x+3x+2x+x=360^{\circ}\Rightarrow 10x=360^{\circ}$ $4x+3x+2x+x=360^{\circ}\Rightarrow 10x=360^{\circ}$

hay $x =36^{\circ}$ $x =36^{\circ}$

d) Ta có: $x+2x=180^{\circ}\Rightarrow 3x=180^{\circ}$ $x+2x=180^{\circ}\Rightarrow 3x=180^{\circ}$hay $x=60^{\circ}$ $x=60^{\circ}$

Bài tập 2 trang 71 sgk Toán 8 tập 1 CTST: Cho tứ giác ABCD có AB = CD, BD là tia phân giác góc B. Chứng minh rằng ABCD là hình thang

Bài giải

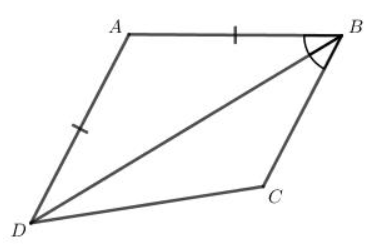
Giải Bài tập 2 trang 71 sgk Toán 8 tập 1 Chân trời

Xét tam giác ABD có AB=AD(gt)

⇒ΔABD cân tại A ⇒ $\widehat{ABD}=\widehat{ADB}$ $\widehat{ABD}=\widehat{ADB}$

Mà $\widehat{ADB}=\widehat{DBC}$ $\widehat{ADB}=\widehat{DBC}$ (BD là tia phân giác của góc B)

Do đó $\widehat{ADB}=\widehat{DBC}$ $\widehat{ADB}=\widehat{DBC}$

Mà $\widehat{ADB};\widehat{DBC}$ $\widehat{ADB};\widehat{DBC}$ so le trong ⇒AD//BC

Vậy ABCD là hình thang.

Bài tập 3 trang 72 sgk Toán 8 tập 1 CTST: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.

a) Chứng minh rằng tứ giác BCMN là hình thang.

b) Chứng mình rằng BN = MN.

Bài giải

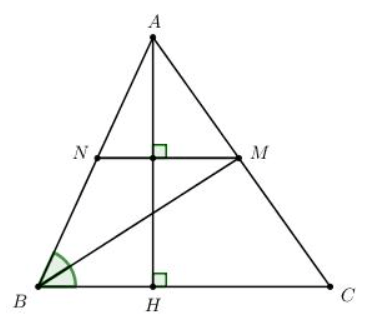
Giải Bài tập 3 trang 72 sgk Toán 8 tập 1 Chân trời

a) Ta có: MN⊥AH(gt)

Và BC⊥AH (AH là đường cao của tam giác ABC) ⇒MN//BC

Suy ra BCMN là hình thang

b) $\widehat{NBM}=\widehat{MBC}$ $\widehat{NBM}=\widehat{MBC}$ (BM là tia phân giác góc B)

Suy ra $\widehat{BMN}=\widehat{NBM}$ $\widehat{BMN}=\widehat{NBM}$⇒ ΔBMN cân tại N.

Vậy BN=MN

Bài tập 4 trang 72 sgk Toán 8 tập 1 CTST: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.

a) Chứng minh rằng: $Δ A B D = Δ E B D$

b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.

c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông.

Bài giải

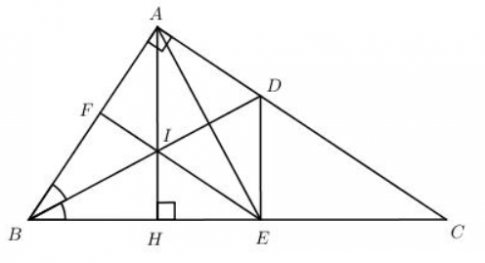
Giải Bài tập 4 trang 72 sgk Toán 8 tập 1 Chân trời

a) Xét ΔABD và ΔEBD ta có:

AB = BE (gt)

BD là cạnh chung

$\widehat{ABD}=\widehat{DBE}$ $\widehat{ABD}=\widehat{DBE}$ (BD là tia phân giác của góc B)

Do đó ΔABD = ΔEBD(c.g.c)

b) Ta có: $\widehat{DEB}=\widehat{BAD}$ $\widehat{DEB}=\widehat{BAD}$(ΔEBD=ΔABD)

Mà $\widehat{BAD}=90^{\circ}$ $\widehat{BAD}=90^{\circ}$

(ΔABD vuông tại A)

Nên $\widehat{DEB}=90^{\circ}$ $\widehat{DEB}=90^{\circ}$ ⇒DE⊥BC

Mặt khác AH⊥BC (gt) do đó DE // AH

⇒ Tứ giác ADEH là hình thang

Lại có $\widehat{AHE}=90^{\circ}$ $\widehat{AHE}=90^{\circ}$ (AH⊥BC)

Vậy tứ giác ADEH là hình thang vuông.

c) Ta có BE=BA(gt)⇒ cân tại B.

Mà BD là tia phân giác của góc B. Do đó BD là đường cao của tam giác BAE.

ΔBAEcó AH, BD là hai đường cao cắt nhau tại I ⇒I là trực tâm của tam giác BAE.

⇒ EFlà đường cao của tam giác BAE

⇒ EF⊥AB

Mà AC⊥AB⇒EF//AC

Vậy tứ giác ACEF là hình thang.

Mà $\widehat{CAF}=90^{\circ}$ $\widehat{CAF}=90^{\circ}$. Do đó tứ giác ACEF là hình thang vuông.

Bài tập 5 trang 72 sgk Toán 8 tập 1 CTST: Tứ giác nào trong Hình 15 là hình thang cân?

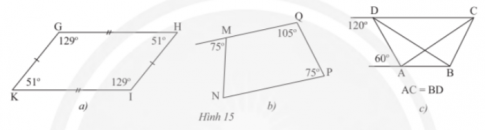
Giải Bài tập 5 trang 72 sgk Toán 8 tập 1 Chân trời

Bài giải

a) Ta có: $\widehat{G}+\widehat{K}=129^{\circ}+51^{\circ}=180^{\circ}$ $\widehat{G}+\widehat{K}=129^{\circ}+51^{\circ}=180^{\circ}$. Mà $\widehat{G};\widehat{K}$ $\widehat{G};\widehat{K}$ là hai góc trong cùng phía suy ra GH // KI ⇒ GHKI là hình thang

$\widehat{G}\neq \widehat{H}$ $\widehat{G}\neq \widehat{H}$

$\widehat{K}\neq \widehat{I}$ $\widehat{K}\neq \widehat{I}$

Suy ra GHIK không là hình thang cân

b) Ta có: $\widehat{NMQ}+\widehat{M}_{ngoài}=180^{\circ}$ $\widehat{NMQ}+\widehat{M}_{ngoài}=180^{\circ}$ (hai góc kề bù)

Do đó $\widehat{NMQ}+75^{\circ}=180^{\circ}\Rightarrow \widehat{NMQ}=180^{\circ}-75^{\circ}=105^{\circ}$ $\widehat{NMQ}+75^{\circ}=180^{\circ}\Rightarrow \widehat{NMQ}=180^{\circ}-75^{\circ}=105^{\circ}$

Ta có: $\widehat{Q}+\widehat{P}=105^{\circ}+75^{\circ}=180^{\circ}$ $\widehat{Q}+\widehat{P}=105^{\circ}+75^{\circ}=180^{\circ}$. Mà $\widehat{Q};\widehat{P}$ $\widehat{Q};\widehat{P}$ là hai góc trong cùng phía suy ra MQ // PN ⇒MQPN là hình thang

Lại có: $\widehat{Q}=\widehat{QMN}(=105^{\circ})$ $\widehat{Q}=\widehat{QMN}(=105^{\circ})$ Do đó MQPN là hình thang cân

c) Ta có: $\widehat{D}_{ngoài}+\widehat{A}_{ngoài}=120^{\circ}+60^{\circ}=180^{\circ}$ $\widehat{D}_{ngoài}+\widehat{A}_{ngoài}=120^{\circ}+60^{\circ}=180^{\circ}$. Mà $\widehat{D}_{ngoài}$ $\widehat{D}_{ngoài}$ và $\widehat{A}_{ngoài}$ $\widehat{A}_{ngoài}$ là hai góc trong cùng phía suy ra AB // CD⇒ABCD là hình thang

Lại có AC = BD suy ra ABCD là hình thang cân

Bài tập 6 trang 72 sgk Toán 8 tập 1 CTST: Cho hình thang ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác góc CEB.

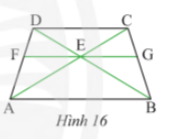
Giải Bài tập 6 trang 72 sgk Toán 8 tập 1 Chân trời

Bài giải

Xét tam giác ACD và BDC ta có:

AD = BC (gt)

AC = BD (gt)

CD chung

Suy ra $\Delta ACD=\Delta BDC$ $\Delta ACD=\Delta BDC$ (c.c.c)

$\Rightarrow \widehat{ACD}=\widehat{BDC}$ $\Rightarrow \widehat{ACD}=\widehat{BDC}$

Ta có: FG // CD suy ra $\widehat{BEG}=\widehat{BDC}$ $\widehat{BEG}=\widehat{BDC}$ (đồng vị), $\widehat{GEC}=\widehat{ACD}$ $\widehat{GEC}=\widehat{ACD}$ (so le trong)

Suy ra $\widehat{BEG}=\widehat{GEC}$ $\widehat{BEG}=\widehat{GEC}$ hay EG là tia phân giác góc CEB.

Bài tập 7 trang 72 sgk Toán 8 tập 1 CTST: Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là 60 cm, cạnh bên là 61 cm và đáy lớn là 92 cm. Tính độ dài đáy nhỏ

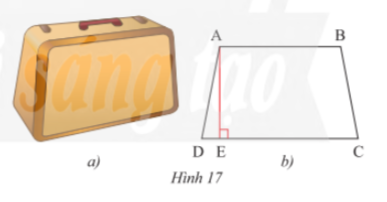
Giải Bài tập 7 trang 72 sgk Toán 8 tập 1 Chân trời

Bài giải

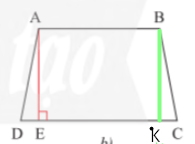
Giải Bài tập 7 trang 72 sgk Toán 8 tập 1 Chân trời

Áp dụng định lí Pythagore cho tam giác ADE vuông tại E ta có:

$AD^{2}=AE^{2}+DE^{2}\Rightarrow DE^{2}=AD^{2}-AE^{2}=61^{2}-60^{2}=121$ $AD^{2}=AE^{2}+DE^{2}\Rightarrow DE^{2}=AD^{2}-AE^{2}=61^{2}-60^{2}=121$ do đó DE =11 cm

Kẻ BK vuông góc với BC ta có:

AB = EK, DE = KC suy ra AB = EK = 92 - 11 x 2 = 70 (cm)

-------------------------------------

Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 3: Hình thang - Hình thang cân CTST. Trong quá trình học môn Toán lớp 8, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã sưu tầm và chọn lọc thêm phần Đề thi giữa kì 1 lớp 8 hay Đề thi học kì 1 lớp 8 để giúp các bạn học sinh học tốt hơn.

Toán 8 Chân trời sáng tạo bài 4: Hình bình hành - Hình thoi

Toán 8 từ năm học 2023 - 2024 trở đi sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Việc lựa chọn giảng dạy bộ sách nào sẽ tùy thuộc vào các trường. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc sẽ cung cấp lời giải bài tập sách giáo khoa, sách bài tập, trắc nghiệm toán từng bài và các tài liệu giảng dạy, học tập khác. Mời các bạn tham khảo qua đường link bên dưới:

Chia sẻ, đánh giá bài viết

1

2.645

Bài trước

Bài sau