Toán 8 Chân trời sáng tạo bài 4: Phân tích đa thức thành nhân tử

Giải Toán 8 CTST

Giải Toán 8 bài 4: Phân tích đa thức thành nhân tử

1. Phương pháp đặt nhân tử chung
- Khám phá 1 trang 23 Toán 8 Tập 1 CTST
- Thực hành 1 trang 24 sgk Toán 8 tập 1 CTST:
2. Phương pháp sử dụng hằng đẳng thức
3. Phương pháp nhóm hạng tử
4. Giải bài tập trang 25 sgk Toán 8 tập 1 CTST:

Giải Toán 8 Chân trời sáng tạo bài 4: Phân tích đa thức thành nhân tử hướng dẫn giải bài tập trong SGK Toán 8 Chân trời sáng tạo tập 1 trang 23, 24, 25. Mời các em cùng tham khảo để nắm được nội dung bài học.

Khởi động trang 23 Toán 8 Tập 1:

Phát biểu của bạn nữ: “99³ – 99 chia hết cho cả ba số 98, 99 và 100.”

Phát biểu của bạn nam: “Đúng rồi. Vì n³ – n chia hết cho n, n – 1 và n + 1 mà. (n là số tự nhiên, n > 1)”

Phát biểu của hai bạn có đúng không? Vì sao?

Khởi động trang 23 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Hướng dẫn giải:

Ta có: 99³ – 99 = 99.(99² – 1)

= 99.(99² – 1²)

= 99.(99 – 1).(99 + 1)

= 99.98.100

Do đó 99³ – 99 chia hết cho cả ba số 98, 99 và 100.

Ta có: n³ – n = n(n² – 1)

= n.(n – 1).(n + 1)

Do đó n³ – n chia hết cho n, n – 1 và n + 1.

Vậy phát biểu của cả hai bạn đều đúng.

1. Phương pháp đặt nhân tử chung

Khám phá 1 trang 23 Toán 8 Tập 1 CTST

Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tính theo mét).

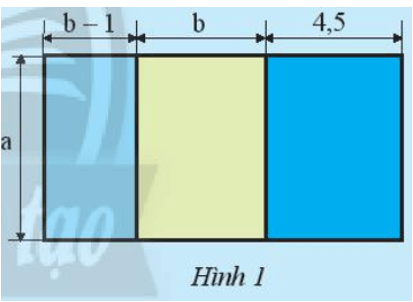
Khám phá 1 trang 23 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Tính theo cách nào nhanh hơn?

Hướng dẫn giải:

Các cách tính diện tích nền nhà là:

Cách 1: $\left( {b - 1 + b + 4,5} \right)a = \left( {2b + 3,5} \right)a = 2ab + 3,5a$ $\left( {b - 1 + b + 4,5} \right)a = \left( {2b + 3,5} \right)a = 2ab + 3,5a$

Cách 2: $\left( {b - 1} \right)a + ba + 4,5a = a.\left( {b - 1 + b + 4,5} \right) = a.\left( {2b + 3,5} \right) = 2ab + 3,5a$ $\left( {b - 1} \right)a + ba + 4,5a = a.\left( {b - 1 + b + 4,5} \right) = a.\left( {2b + 3,5} \right) = 2ab + 3,5a$

Cách 3: $\left( {b - 1} \right)a + ba + 4,5a = ba - a + ba + 4,5a = ba + ba - a + 4,5a = 2ab + 3,5a$ $\left( {b - 1} \right)a + ba + 4,5a = ba - a + ba + 4,5a = ba + ba - a + 4,5a = 2ab + 3,5a$

Tính theo cách 1, 2 nhanh hơn

Thực hành 1 trang 24 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử

$a) P=6x-2x^{3}$ $a) P=6x-2x^{3}$

$b) Q=5x^{3}-15x^{2}y$ $b) Q=5x^{3}-15x^{2}y$

$c) R=3x^{3}y^{3}-6xy^{3}z+xy$ $c) R=3x^{3}y^{3}-6xy^{3}z+xy$

Hướng dẫn giải:

$a) P=6x-2x^{3}=2x\times 3-2x \times x^{2}=2x(3-x^{2})$ $a) P=6x-2x^{3}=2x\times 3-2x \times x^{2}=2x(3-x^{2})$

$b) Q=5x^{3}-15x^{2}y=5x^{2}\times x-5x^{2} \times 3y$ $b) Q=5x^{3}-15x^{2}y=5x^{2}\times x-5x^{2} \times 3y$

$=5x^{2}(x-3y)$ $=5x^{2}(x-3y)$

$c) R=3x^{3}y^{3}-6xy^{3}z+xy=xy\times 3x^{2}y^{2}- xy \times 6y^{2}z+xy$ $c) R=3x^{3}y^{3}-6xy^{3}z+xy=xy\times 3x^{2}y^{2}- xy \times 6y^{2}z+xy$

$=xy(3x^{2}y^{2}-6y^{2}z+1)$ $=xy(3x^{2}y^{2}-6y^{2}z+1)$

2. Phương pháp sử dụng hằng đẳng thức

Khám phá 2 trang 24 Toán 8 Tập 1 CTST

Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:

a) $4{x^2} - 9$ $4{x^2} - 9$;

b) ${x^2}{y^2} - \dfrac{1}{4}{y^2}$ ${x^2}{y^2} - \dfrac{1}{4}{y^2}$

Hướng dẫn giải::

a) $4{x^2} - 9 = {\left( {2x} \right)^2} - {3^2} = \left( {2x + 3} \right)\left( {2x - 3} \right)$ $4{x^2} - 9 = {\left( {2x} \right)^2} - {3^2} = \left( {2x + 3} \right)\left( {2x - 3} \right)$

b) ${x^2}{y^2} - \dfrac{1}{4}{y^2} = {\left( {xy} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = \left( {xy + \dfrac{1}{2}y} \right)\left( {xy - \dfrac{1}{2}y} \right) = y\left( {x + \dfrac{1}{2}} \right)y\left( {x - \dfrac{1}{2}} \right) = {y^2}\left( {x + \dfrac{1}{2}} \right)\left( {x - \dfrac{1}{2}} \right)$ ${x^2}{y^2} - \dfrac{1}{4}{y^2} = {\left( {xy} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = \left( {xy + \dfrac{1}{2}y} \right)\left( {xy - \dfrac{1}{2}y} \right) = y\left( {x + \dfrac{1}{2}} \right)y\left( {x - \dfrac{1}{2}} \right) = {y^2}\left( {x + \dfrac{1}{2}} \right)\left( {x - \dfrac{1}{2}} \right)$

Thực hành 2 trang 24 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) 9x^{2}-16$ $a) 9x^{2}-16$

$b) 4x^{2}-12xy+9y^{2}$ $b) 4x^{2}-12xy+9y^{2}$

$c) t^{3}-8$ $c) t^{3}-8$

$d) 3ax^{3}y^{3}+2a$ $d) 3ax^{3}y^{3}+2a$

Hướng dẫn giải:

$a) 9x^{2}-16=(3x)^{2}-4^{2}=(3x-4)(3x+4)$ $a) 9x^{2}-16=(3x)^{2}-4^{2}=(3x-4)(3x+4)$

$b) 4x^{2}-12xy+9y^{2}=(2x)^{2}-2\times 2x\times 3y+(3y)^{2}$ $b) 4x^{2}-12xy+9y^{2}=(2x)^{2}-2\times 2x\times 3y+(3y)^{2}$

$=(2x-3y)^{2}$ $=(2x-3y)^{2}$

$c) t^{3}-8=t^{3}-2^{3}$ $c) t^{3}-8=t^{3}-2^{3}$

$=(t-2)(t^{2}+2t+4)$ $=(t-2)(t^{2}+2t+4)$

$d) 3ax^{3}y^{3}+2a=2a(x^{3}y^{3}+1)$ $d) 3ax^{3}y^{3}+2a=2a(x^{3}y^{3}+1)$

$=2a(xy+1)(x^{2}y^{2}-xy+1)$ $=2a(xy+1)(x^{2}y^{2}-xy+1)$

Vận dụng 1 trang 24 sgk Toán 8 tập 1 CTST:

Tìm một hình hộp chữ nhật có thể tích $2x^{3}-18x$ $2x^{3}-18x$ (với x > 3) mà độ dài các cạnh đều là biểu thức chứa x

Hướng dẫn giải:

Ta có: $2x^{3}-18x=2x(x^{2}-9)=2x(x-3)(x+3)$ $2x^{3}-18x=2x(x^{2}-9)=2x(x-3)(x+3)$

Độ dài các cạnh của hình hộp chữ nhật cần tìm lần lượt là: 2x, x - 3, x + 3

Vận dụng 2 trang 24 sgk Toán 8 tập 1 CTST:

Giải đáp câu hỏi trang 23

Hướng dẫn giải:

Ta có: $n^{3}-n=n(n^{2}-1)=n(n-1)(n+1)$ $n^{3}-n=n(n^{2}-1)=n(n-1)(n+1)$

Vì vậy $n^{3}-n$ chia hết cho n, n - 1 và n + 1 (n là số tự nhiên, n > 1)

Vậy phát biểu của hai bạn là đúng

3. Phương pháp nhóm hạng tử

Khám phá 3 trang 24 Toán 8 Tập 1 CTST

Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:

${a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...$ ${a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...$

Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Hướng dẫn giải::

${a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = a\left( {a + b} \right) + 2\left( {a + b} \right) = \left( {a + b} \right)\left( {a + 2} \right)$ ${a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = a\left( {a + b} \right) + 2\left( {a + b} \right) = \left( {a + b} \right)\left( {a + 2} \right)$

Cách khác:

${a^2} + ab + 2a + 2b = \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) = a\left( {a + 2} \right) + b\left( {a + 2} \right) = \left( {a + 2} \right)\left( {a + b} \right)$ ${a^2} + ab + 2a + 2b = \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) = a\left( {a + 2} \right) + b\left( {a + 2} \right) = \left( {a + 2} \right)\left( {a + b} \right)$

Thực hành 3 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) a^{3}-a^{2}b+a-b$ $a) a^{3}-a^{2}b+a-b$

$b) x^{3}+2x^{2}-xy^{2}-2y^{2}$ $b) x^{3}+2x^{2}-xy^{2}-2y^{2}$

Hướng dẫn giải:

$a) a^{3}-a^{2}b+a-b=(a^{3}+a)-(a^{2}b+b)$ $a) a^{3}-a^{2}b+a-b=(a^{3}+a)-(a^{2}b+b)$

$=a(a^{2}+1)-b(a^{2}+1)=(a-b)(a^{2}+1)$ $=a(a^{2}+1)-b(a^{2}+1)=(a-b)(a^{2}+1)$

$b) x^{3}+2x^{2}-xy^{2}-2y^{2}=(x^{3}-xy^{2})+(2x^{2}-2y^{2})$ $b) x^{3}+2x^{2}-xy^{2}-2y^{2}=(x^{3}-xy^{2})+(2x^{2}-2y^{2})$

$=x(x^{2}-y^{2})+2(x^{2}-y^{2})=(x+2)(x-y)(x+y)$ $=x(x^{2}-y^{2})+2(x^{2}-y^{2})=(x+2)(x-y)(x+y)$

Vận dụng 3 trang 25 sgk Toán 8 tập 1 CTST:

Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).

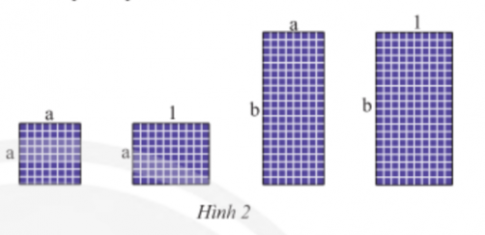
Giải Vận dụng 3 trang 25 sgk Toán 8 tập 1 Chân trời

Hướng dẫn giải:

Có thể ghép bốn tấm pin mặt trời thành một hình chữ nhật

Ta có hình chữ nhật có kích thước các cạnh là: a + 1, a + b

Khi a = 0,8, b = 2, kích thước các cạnh là: 1,8 m và 2,8 m

Diện tích hình chữ nhật là: 1,8 x 2,8 = 5,04 (m²)

4. Giải bài tập trang 25 sgk Toán 8 tập 1 CTST:

Bài tập 1 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) x^{3}+4x$ $a) x^{3}+4x$

$b) 6ab-9ab^{2}$ $b) 6ab-9ab^{2}$

$c) 2a(x-1)+3b(1-x)$

$d) (x-y)^{2}-x(y-x)$ $d) (x-y)^{2}-x(y-x)$

Hướng dẫn giải:

$a) x^{3}+4x=x(x^{2}+4)$ $a) x^{3}+4x=x(x^{2}+4)$

$b) 6ab-9ab^{2}=3ab(2-3b)$ $b) 6ab-9ab^{2}=3ab(2-3b)$

$c) 2a(x-1)+3b(1-x)=2a(x-1)-3b(x-1)$

$=(2a-3b)(x-1)$

$d) (x-y)^{2}-x(y-x)=(x-y)^{2}+x(x-y)$ $d) (x-y)^{2}-x(y-x)=(x-y)^{2}+x(x-y)$

$=(x-y+x)(x-y)=(2x-y)(x-y)$

Bài tập 2 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) 4x^{2}-1$ $a) 4x^{2}-1$

$b) (x+2)^{2}-9$ $b) (x+2)^{2}-9$

$c) (a+b)^{2}-(a-2b)^{2}$ $c) (a+b)^{2}-(a-2b)^{2}$

Hướng dẫn giải:

$a) 4x^{2}-1=(2x)^{2}-1=(2x-1)(2x+1)$ $a) 4x^{2}-1=(2x)^{2}-1=(2x-1)(2x+1)$

$b) (x+2)^{2}-9=(x+2)^{2}-3^{2}$ $b) (x+2)^{2}-9=(x+2)^{2}-3^{2}$

$=(x+2-3)(x+2+3)=(x-1)(x+5)$

$c) (a+b)^{2}-(a-2b)^{2}=(a+b-a+2b)(a+b+a-2b)$ $c) (a+b)^{2}-(a-2b)^{2}=(a+b-a+2b)(a+b+a-2b)$

$=3b(2a-b)$

Bài tập 3 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) 4a^{2}+4a+1$ $a) 4a^{2}+4a+1$

$b) -3x^{2}+6xy-3y^{2}$ $b) -3x^{2}+6xy-3y^{2}$

$c) (x+y)^{2}-2(x+y)z+z^{2}$ $c) (x+y)^{2}-2(x+y)z+z^{2}$

Hướng dẫn giải:

$a) 4a^{2}+4a+1=(2a)^{2}+2\times 2a+1=(2a+1)^{2}$ $a) 4a^{2}+4a+1=(2a)^{2}+2\times 2a+1=(2a+1)^{2}$

$b) -3x^{2}+6xy-3y^{2}=-[(\sqrt{3}x)^{2}-2\times \sqrt{3}x \times \sqrt{3}y+(\sqrt{3}y)^{2}]$ $b) -3x^{2}+6xy-3y^{2}=-[(\sqrt{3}x)^{2}-2\times \sqrt{3}x \times \sqrt{3}y+(\sqrt{3}y)^{2}]$

$=-(\sqrt{3}x-\sqrt{3}y)^{2}$ $=-(\sqrt{3}x-\sqrt{3}y)^{2}$

$c) (x+y)^{2}-2(x+y)z+z^{2}=(x+y-z)^{2}$ $c) (x+y)^{2}-2(x+y)z+z^{2}=(x+y-z)^{2}$

Bài tập 4 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) 8x^{3}-1$ $a) 8x^{3}-1$

$b) x^{3}+27y^{3}$ $b) x^{3}+27y^{3}$

$c) x^{3}-y^{6}$ $c) x^{3}-y^{6}$

Hướng dẫn giải:

$a) 8x^{3}-1=(2x)^{3}-1=(2x-1)[(2x)^{2}+2x+1]$ $a) 8x^{3}-1=(2x)^{3}-1=(2x-1)[(2x)^{2}+2x+1]$

$=(2x-1)(4x^{2}+2x+1)$ $=(2x-1)(4x^{2}+2x+1)$

$b) x^{3}+27y^{3}=x^{3}+(3y)^{3}=(x+3y)(x^{2}-3xy+9y^{2})$ $b) x^{3}+27y^{3}=x^{3}+(3y)^{3}=(x+3y)(x^{2}-3xy+9y^{2})$

$c) x^{3}-y^{6}=x^{3}-(y^{2})^{3}=(x-y^{2})(x^{2}+xy^{2}+y^{4})$ $c) x^{3}-y^{6}=x^{3}-(y^{2})^{3}=(x-y^{2})(x^{2}+xy^{2}+y^{4})$

Bài tập 5 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) 4x^{3}-16x$ $a) 4x^{3}-16x$

$b) x^{4}-y^{4}$ $b) x^{4}-y^{4}$

$c) xy^{2}+x^{2}y+\frac{1}{4}y^{3}$ $c) xy^{2}+x^{2}y+\frac{1}{4}y^{3}$

$d) x^{2}+2x-y^{2}+1$ $d) x^{2}+2x-y^{2}+1$

Hướng dẫn giải:

$a) 4x^{3}-16x=4x(x^{2}-4)=4x(x-2)(x+2)$ $a) 4x^{3}-16x=4x(x^{2}-4)=4x(x-2)(x+2)$

$b) x^{4}-y^{4}=(x^{2}-y^{2})(x^{2}+y^{2})=(x-y)(x+y)(x^{2}+y^{2})$ $b) x^{4}-y^{4}=(x^{2}-y^{2})(x^{2}+y^{2})=(x-y)(x+y)(x^{2}+y^{2})$

$c) xy^{2}+x^{2}y+\frac{1}{4}y^{3}=y(xy+x^{2}+\frac{1}{4}y^{2})$ $c) xy^{2}+x^{2}y+\frac{1}{4}y^{3}=y(xy+x^{2}+\frac{1}{4}y^{2})$

$=y(x+\frac{1}{2}y)^{2}$ $=y(x+\frac{1}{2}y)^{2}$

$d) x^{2}+2x-y^{2}+1=(x^{2}+2x+1)-y^{2}$ $d) x^{2}+2x-y^{2}+1=(x^{2}+2x+1)-y^{2}$

$=(x+1)^{2}-y^{2}=(x+1-y)(x+1+y)$ $=(x+1)^{2}-y^{2}=(x+1-y)(x+1+y)$

Bài tập 6 trang 25 sgk Toán 8 tập 1 CTST:

Phân tích các đa thức sau thành nhân tử:

$a) x^{2}-xy+x-y$ $a) x^{2}-xy+x-y$

$b) x^{2}+2xy-4x-8y$ $b) x^{2}+2xy-4x-8y$

$c) x^{3}-x^{2}-x+1$ $c) x^{3}-x^{2}-x+1$

Hướng dẫn giải:

$a) x^{2}-xy+x-y=(x^{2}-xy)+(x-y)$ $a) x^{2}-xy+x-y=(x^{2}-xy)+(x-y)$

$=x(x-y)+(x-y)=(x+1)(x-y)$

$b) x^{2}+2xy-4x-8y=(x^{2}-4x)+(2xy-8y)$ $b) x^{2}+2xy-4x-8y=(x^{2}-4x)+(2xy-8y)$

$=x(x-4)+2y(x-4)=(x+2y)(x-4)$

$c) x^{3}-x^{2}-x+1=(x^{3}+1)-(x^{2}+x)$ $c) x^{3}-x^{2}-x+1=(x^{3}+1)-(x^{2}+x)$

$=(x+1)(x^{2}-x+1)-x(x+1)=(x+1)(x^{2}-2x+1)$ $=(x+1)(x^{2}-x+1)-x(x+1)=(x+1)(x^{2}-2x+1)$

Bài tập 7 trang 25 sgk Toán 8 tập 1 CTST:

Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng $49y^{2}+28y+4$ $49y^{2}+28y+4$

Hướng dẫn giải:

$49y^{2}+28y+4=(7y)^{2}+2\times 7y \times 2+2^{2}$ $49y^{2}+28y+4=(7y)^{2}+2\times 7y \times 2+2^{2}$

$=(7y+2)^{2}$ $=(7y+2)^{2}$

Vậy cạnh của hình vuông bằng 7y + 2

Trắc nghiệm Toán 8 CTST bài 4

Bài trắc nghiệm số: 4781

Bài tiếp theo: Toán 8 Chân trời sáng tạo bài 5: Phân thức đại số

Chia sẻ, đánh giá bài viết

7

3.732

Bài trước

Bài sau

Chia sẻ bởi:
Nai Con
Ngày: 07/11/2024

Tải về

Chọn file muốn tải về: