VnDoc.com

Toán 8 Chân trời sáng tạo Bài 2: Các trường hợp đồng dạng của hai tam giác

Giải Toán 8 CTST

Bài trước

Bài sau

Giải Toán 8 CTST Bài 2: Các trường hợp đồng dạng của hai tam giác

Giải Toán 8 Chân trời sáng tạo Bài 2 Các trường hợp đồng dạng của hai tam giác tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

Hoạt động 1

Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M,N sao cho AM = 2cm,AN = 3cm.

a) So sánh các tỉ số $\frac{{A$ $\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}.$

b) Tính độ dài đoạn thẳng MN.

c) Em có nhận xét gì về mối liên hệ giữa các tam giác ABC,AMN và A'B'C'?

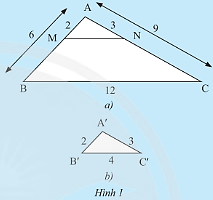
Hướng dẫn trả lời:

a) Ta có: $\frac{{A$ $\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}$. Do đó, các tỉ số trên bằng nhau.

b) Ta có: $\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}$ $\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}$

Vì $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC$ (định lí Thales đảo)

Vì $MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}$ $MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}$ (Hệ quả của định lí Thales)

Do đó, $\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4.$ $\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4.$

Vậy MN = 4cm.

c) Vì MN//BC $\Rightarrow \Delta ABC\backsim\Delta AMN$ $\Rightarrow \Delta ABC\backsim\Delta AMN$ (định lí)(1)

Xét tam giác AMN và tam giác A'B'C' ta có:

AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm

Do đó, $\Delta AMN = \Delta A$ $\Delta AMN = \Delta A'B'C'$ (c.c.c)

Vì $\Delta AMN = \Delta A$ $\Delta AMN = \Delta A'B'C'$ nên $\Delta AMN\backsim\Delta A$ $\Delta AMN\backsim\Delta A'B'C'$ (2)

Từ (1) và (2) suy ra, $\Delta ABC\backsim\Delta A$ $\Delta ABC\backsim\Delta A'B'C'.$

Thực hành 1

Tìm trong Hình 4 các cặp tam giác đồng dạng

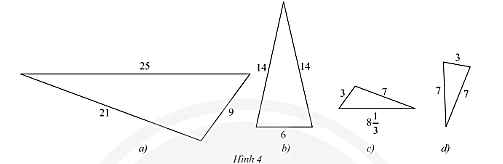
Hướng dẫn trả lời:

Xét cặp tam giác thứ nhất: Hình a và Hình c.

Ta có: $\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}.$ $\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}.$

Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.

Xét cặp tam giác thứ hai: Hình b và Hình d.

Ta có: $\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}.$ $\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}.$

Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.

Hoạt động 2

Cho tam giác DEF và tam giác ABC có $DE = \frac{1}{3}AB$ $DE = \frac{1}{3}AB$, $DF = \frac{1}{3}AC,\widehat D = \widehat A$ $DF = \frac{1}{3}AC,\widehat D = \widehat A$ (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ $MN//BC\left( {N \in AC} \right).$ $MN//BC\left( {N \in AC} \right).$

a) So sánh $\frac{{AM}}{{AB}} và \frac{{AN}}{{AC}}$ $\frac{{AM}}{{AB}} và \frac{{AN}}{{AC}}$

b) So sánh AN với DF.

c) Tam giác AMN có đồng dạng với tam giác ABC không?

d) Dự đoán sự đồng dạng của hai tam giác DEF và ABC.

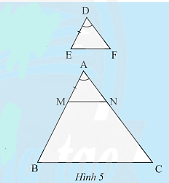
Hướng dẫn trả lời:

a) Vì $MN//BC\left( {M \in AB,N \in AC} \right)$ $MN//BC\left( {M \in AB,N \in AC} \right)$ nên $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$(định lí Thales).

b) Vì AM = DE mà $\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC.$ $\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC.$

Lại có DF = $\frac{1}{3}AC$ $\frac{1}{3}AC$ nên $AN = DF = \frac{1}{3}AC.$ $AN = DF = \frac{1}{3}AC.$

c) Vì $MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN$ $MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN$ (định lí)(1)

d) Dự đoán hai tam giác DEF và ABC đồng dạng.

Thực hành 2

Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8. Chứng minh rằng $\Delta ADE\backsim\Delta ACF.$ $\Delta ADE\backsim\Delta ACF.$

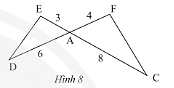
Hướng dẫn trả lời:

Ta có: $\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4};$ $\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4};$

Xét $\Delta ADE$ $\Delta ADE$ và $\Delta ACF$ $\Delta ACF$ có:

$\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}$ $\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}$

$\widehat {EAD} = \widehat {FAC}$ $\widehat {EAD} = \widehat {FAC}$ (hai góc đối đỉnh)

Do đó, $\Delta ADE\backsim\Delta ACF(c.g.c)$ $\Delta ADE\backsim\Delta ACF(c.g.c)$

Vận dụng 2 trang 70 Toán 8 Tập 2: Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở Hoạt động khởi động (trang 67).

Lời giải:

Trường hợp	Giống nhau	Khác nhau
Trường hợp	Giống nhau	Bằng nhau	Đồng dạng
1	3 cạnh	3 cạnh tương ứng bằng nhau	3 cạnh tương ứng tỉ lệ
2	2 cạnh 1 góc	2 cạnh tương ứng và một góc kề với hai cạnh bằng nhau	2 cạnh tương ứng tỉ lệ
3	2 góc bằng nhau	1 cạnh và 2 góc kề tương ứng bằng nhau	Chỉ 2 góc bằng nhau, không cần có điều kiện cạnh

Bài 1 trang 70 Toán 8 Tập 2:

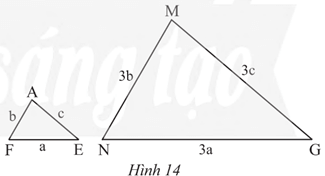
Bài 1 trang 70 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

a) Tam giác AFE và MNG ở Hình 14 có đồng dạng với nhau không? Vì sao?

b) Biết tam giác AFE có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

Bài 2 trang 70 Toán 8 Tập 2: Tam giác ABC có độ dài AB = 4 cm, AC = 6 cm, BC = 9 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.

Bài 3 trang 70 Toán 8 Tập 2: Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 660 m. Nam chạy bốn vòng trên con đường bên trong, Hùng chạy hai vòng trên con đường bên ngoài. So sánh quãng đường chạy được của hai bạn.

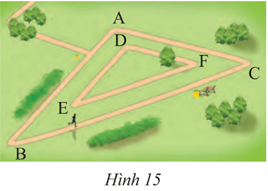
Bài 3 trang 70 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8