Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

Hướng dẫn Giải Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0) thuộc bộ sách Chân trời sáng tạo cung cấp lời giải chi tiết và phương pháp luận khoa học cho các bài tập trong sách giáo khoa. Đây là nguồn tham khảo lý tưởng để các em củng cố tư duy logic, rèn luyện kỹ năng giải toán chính xác và tự tin hơn trong các kỳ kiểm tra. Mời các em cùng khám phá nội dung chi tiết để tối ưu hóa hiệu quả học tập.

1. Hàm số bạc nhất

Khám phá 1 trang 16 Toán 8 Tập 2: Trong thực tế chúng ta thường gặp các mô hình hấp dẫn đến những hàm số có dạng như: y = 2x + 5; y = −x + 4; y = 5x; ... Những hàm số này được gọi là hàm số bậc nhất. Vậy hàm số bậc nhất có dạng như thế nào?

Hướng dẫn giải:

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b với a, b là các số cho trước và a ≠ 0.

Thực hành 1 trang 16 Toán 8 Tập 2: Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số a, b của các hàm số đó: y = 4x − 7; y = x²; y = −6x − 4; y = 4x; y=3/x, s = 5v + 8; m = 30n – 25.

Hướng dẫn giải:

Các hàm số bậc nhất là:

y = 4x − 7 với a = 4 và b = −7

y = −6x − 4 với a = −6 và b = −4

y = 4x với a = 4 và b = 0

s = 5v + 8 với a = 5 và b = 8

m = 30n − 25 với a = 30 và b = −25

Vận dụng 1 trang 16 Toán 8 Tập 2: Một hình chữ nhật có các kích thước là 2 m và 3 m. Gọi y là chu vi của hình chữ nhật này sau khi tăng chiều dài và chiều rộng thêm x (m). Hãy chứng tỏ y là một hàm số bậc nhất theo biến số x. Tìm các hệ số a, b của hàm số này.

Hướng dẫn giải:

Chiều dài sau khi tăng x ( m ) là: 3 + x ( m ) .

Chiều rộng sau khi tăng x ( m ) là: 2 + x ( m ) .

Chu vi hình chữ nhật sau khi chiều dài và chiều rộng tăng là:

y = (3 + x + 2 + x).2 = 4x + 12 (m) .

Suy ra y là một hàm số bâc nhất theo biến số x với a = 4 và b = 12 .

2. Bảng giá trị của hàm số bậc nhất

Khám phá 2 trang 17 Toán 8 Tập 2: Lượng nước y (tính theo m³) có trong một bể nước sau x giờ mở vòi cấp nước được cho bởi hàm số y = 2x + 3. Tính lượng nước có trong bể sau 0 giờ; 1 giờ; 2 giờ; 3 giờ; 10 giờ và hoàn thành bảng giá trị sau:

x	0	1	2	3	10
y = f(x) = 2x + 3	?	?	?	?	?

Hướng dẫn giải:

• Với x = 0 ta có: y = 2.0 + 3 = 3
• Với x = 1 ta có: y = 2.1 + 3 = 5
• Với x = 2 ta có: y = 2.2 + 3 = 7
• Với x = 3 ta có: y = 2.3 + 3 = 9
• Với x = 10 ta có: y = 2.10 + 3 = 23

x	0	1	2	3	10
y = f(x) = 2x + 3	3	5	7	9	23

Thực hành 2 trang 17 Toán 8 Tập 2: Lập bảng giá trị của mỗi hàm số bậc nhất sau:

y = f(x) = 4x − 1 và y = h(x) = −0,5x + 8

với x lần lượt bằng −3; −2; −1; 0; 1; 2; 3.

Hướng dẫn giải:

• Với x = −3 ta có: y = f(−3) = 4.(−3) – 1 = −13;
• Với x = −2 ta có: y = f(−2) = 4.(−2) – 1 = −9;
• Với x = −1 ta có: y = f(−1) = 4.(−1) – 1 = −5;
• Với x = 0 ta có: y = f(0) = 4.0 – 1 = −1;
• Với x = 1 ta có: y = f(1) = 4.1 – 1 = 3;
• Với x = 2 ta có: y = f(2) = 4.2 – 1 = 7;
• Với x = 3 ta có: y = f(3) = 4.3 – 1 = 11;
• Với x = −3 ta có: y = h(−3) = −0,5.(−3) + 8 = 9,5;
• Với x = −2 ta có: y = h(−2) = −0,5.(−3) + 8 = 9;
• Với x = −1 ta có: y = h(−1) = −0,5.(−3) + 8 = 8,5;
• Với x = 0 ta có: y = h(0) = −0,5.0 + 8 = 8;
• Với x = 1 ta có: y = h(1) = −0,5.1 + 8 = 7,5;
• Với x = 2 ta có: y = h(2) = −0,5.2 + 8 = 7;
• Với x = 3 ta có: y = h(3) = −0,5.3 + 8 = 6,5.

Ta có bảng giá trị sau:

x	−3	−2	−1	0	1	2	3
y = 4x – 1	−13	−9	−5	−1	3	7	11

x	−3	−2	−1	0	1	2	3
y = −0,5x + 8	9,5	9	8,5	8	7,5	7	6,5

Vận dụng 2 trang 17 Toán 8 Tập 2: Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố Đà Nẵng với tốc độ 40 km/h (Hình 2)

a) Biết rằng bến xe cách bưu điện thành phố Nha Trang 6 km. Sau x giờ, xe khách cách bưu điện thành phố y km. Tính y theo x.

b) Chứng minh rằng y là một hàm số bậc nhất theo biến số x.

c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này:

x	0	1	2	3
y	?	?	?	?

Hướng dẫn giải:

a) Quãng đường đi được sau x giờ là : 40x (km)

Vậy sau x giờ, xe khách cách bưu điện thành phố là : y = 40x + 6 (km)

1. b) Vì y có dạng y = ax + b và a ≠ 0 nên y là hàm số bậc nhất theo biến số x.
2. c)

• Với x = 0 ta có y = 40.0 + 6 = 6
• Với x = 1 ta có y = 40.1 + 6 = 46
• Với x = 2 ta có y = 40.2 + 6 = 86
• Với x = 3 ta có y = 40.3 + 6 = 126

Ta có bảng giá trị sau:

x	0	1	2	3
y	6	46	86	126

Ý nghĩa:

- Tại điểm khởi hành, xe khách cách bưu điện thành phố Nha Trang 6 km.

- Sau khi đi được 1 giờ xe khách cách bưu điện thành phố Nha Trang 46 km.

- Sau khi đi được 2 giờ xe khách cách bưu điện thành phố Nha Trang 86 km.

- Sau khi đi được 3 giờ xe khách cách bưu điện thành phố Nha Trang 126 km.

Bài tập

Bài 1 trang 22 Toán 8 tập 2 CTST

Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số a, b của chúng

a) y = 4x + 2;

b) y = 5 – 3x;

c) y = 2 + x2;

d) y = −0,2x;

e.

Gợi ý đáp án

a) y = 4x + 2 là hàm số bậc nhất với a = 4, b = 2.

b) y = 5 – 3x là hàm số bậc nhất với a = −3, b = 5

c) y= 2 + x2 không là hàm số bậc nhất.

d) y = −0,2x là hàm số bậc nhất với a = y = −0,2, b = 0.

e. là hàm số bậc nhất với a= b = −1.

bài 3 trang 22 Toán 8 Tập 2 CTST

Với giá trị nào của m thì mỗi hàm số sau đây là hàm số bậc nhất?

a) y = (m − 1)x + m;

b) y = 3 − 2mx.

Hướng dẫn giải:

a) Điều kiện để hàm số y = (m − 1)x + m là hàm số bậc nhất là m − 1 ≠ 0 hay m ≠ 1.

b) Điều kiện để hàm số y = 3 − 2mx là hàm số bậc nhất là −2m ≠ 0 hay m ≠ 0.

Bài 3 trang 22 Toán 8 tập 2 CTST

a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

y = x; y = x + 2; y = −x; y = −x + 2 .

b) Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích.

Gợi ý đáp án

a) • Với hàm số y = x, cho x = 1 thì y = 1.

Đồ thị hàm số y = x đi qua các điểm O(0; 0) và C(1; 1).

• Với hàm số y = x + 2, cho x = 0 thì y = 2, cho x = −1 thì y = 1.

Đồ thị hàm số y = x + 2 đi qua các điểm B(0; 2) và A(−1; 1).

• Với hàm số y = −x, cho x = −1 thì y = 1.

Đồ thị hàm số y = −x đi qua các điểm O(0; 0) và A(−1; 1).

• Với hàm số y = −x + 2, cho x = 0 thì y = 2, cho x = 1 thì y = 1.

Đồ thị hàm số y = −x + 2 đi qua các điểm B (0; 2) và C(1; 1).

b) Ta có: Đường thẳng y = x song song với đường thẳng y = x + 2 suy ra OC // AB .

Đường thẳng y = −x song song với đường thẳng y = −x + 2 suy ra OA // BC .

Tứ giác OABC có: OC // AB, OA // BC

Suy ra tứ giác OABC là hình bình hành .

Hình bình hành OABC có hai đường chéo OB và AC vuông góc và bằng nhau nên tứ giác OABC là hình vuông.

Bài 5 trang 22 Toán 8 tập 2 CTST

Gọi C và r lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ C là một hàm số bậc nhất theo biến số r. Tìm hệ số a, b của hàm số này.

Gợi ý đáp án

Công thức tính chu vi hình tròn là: C = 2πr

Hàm số C = 2πr có dạng y = ax + b với a = 2π ≠ 0 và b = 0 nên C là một hàm số bậc nhất theo biến số r.

Bài 6 trang 22 Toán 8 tập 2 CTST

Một người đi bộ trên đường thẳng với tốc độ v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ).

a) Lập công thức tính s theo t.

b) Vẽ đồ thị của hàm số s theo biến số t khi v = 4.

Gợi ý đáp án

a) s = vt.

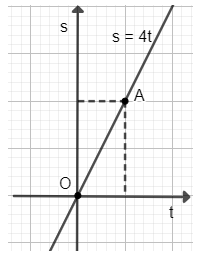
b) Hàm số: s = 4t.

Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); A(1; 4).