Toán 8 Chân trời sáng tạo Bài tập cuối chương 8
Giải Toán 8 Chân trời sáng tạo Bài tập cuối chương 8 tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.
Giải Toán 8 CTST Bài tập cuối chương 8
Bài 1 trang 84 Toán 8 Tập 2:
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai tam giác đồng dạng thì bằng nhau.
B. Hai tam giác bằng nhau thì đồng dạng.
C. Hai tam giác bằng nhau thì không đồng dạng.
D. Hai tam giác cân thì luôn đồng dạng.
Hướng dẫn giải
Đáp án đúng là: B
Hai tam giác bằng nhau thì đồng dạng với theo tỉ số k = 1.
Bài 2 trang 84 Toán 8 Tập 2:
Nếu ΔABC ᔕ ΔMNP theo tỉ số k = 3 thì ΔMNP ᔕ ΔABC theo tỉ số
A. 1/3
B. 1/9
C. 3.
D. 9.
Hướng dẫn giải
Đáp án đúng là: A
Ta có ΔABC ᔕ ΔMNP theo tỉ số k = 3.
Do đó ΔMNP ᔕ ΔABC theo tỉ số 1/k=1/3
Bài 3 trang 84 Toán 8 Tập 2:
Nếu tam giác ABC có MN // AB (với M ∈ AC, N ∈ BC) thì
A. ΔCMN ᔕ ΔABC.
B. ΔCNM ᔕ ΔCAB.
C. ΔCNM ᔕ ΔABC.
D. ΔMNC ᔕ ΔABC.
Hướng dẫn giải
Đáp án đúng là: D
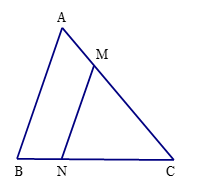
Xét tam giác ABC có MN // AB nên ΔMNC ᔕ ΔABC.
Bài 4 trang 84 Toán 8 Tập 2:
Cho ΔABD ᔕ ΔDEF với tỉ số đồng dạng k=1/3, biết AB = 9 cm. Khi đó DE bằng
A. 6 cm.
B. 12 cm.
C. 3 cm.
D. 27 cm.
Hướng dẫn giải
Đáp án đúng là: D
Bài 6 trang 84 Toán 8 Tập 2:
Cho ΔXYZ ᔕ ΔEFG, biết XY = 6 cm; EF = 8 cm; EG = 12 cm. Khi đó XZ bằng
A. 10 cm.
B. 9 cm.
C. 12 cm.
D. 16 cm.
Hướng dẫn giải
Đáp án đúng là: B
Bài 7 trang 84 Toán 8 Tập 2:
Cho ΔABC ᔕ ΔDEF, biết A^=85o, B^=600. khi đó số đo góc F bằng
A. 60°.
B. 85°.
C. 35°.
D. 45°.
Hướng dẫn giải
Đáp án đúng là: C
Bài 8 trang 84 Toán 8 Tập 2:
Cho hình thang ABCD (AB // CD), có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 8 cm, CD = 20 cm. Khi đó ΔAOB ᔕ ΔCOD với tỉ số đồng dạng là
A. k=2/3.
B. k=3/2
C. k=2/5
D. k=5/2
Hướng dẫn giải
Đáp án đúng là: C
Bài 9 trang 84 Toán 8 Tập 2:
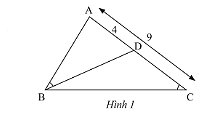
Trong Hình 1, cho biết 
\(\widehat {ABD} = \widehat {ACB}\),AC = 9cm,AD = 4cm.
a) Chứng minh tam giác \Delta ABD\backsim\Delta ACB.
b) Tính độ dài cạnh AB.
Hướng dẫn giải
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB (g.g)\)
b) Vì \Delta ABD\backsim\Delta ACB
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy AB = 6cm.
