Toán 8 Bài 4: Hệ số góc của đường thẳng

Giải Toán 8 Chân trời sáng tạo bài 4: Hệ số góc của đường thẳng tổng hợp đáp án cho các câu hỏi trong SGK Toán 8 Chân trời sáng tạo, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

Khởi động trang 23 Toán 8 Tập 2:

Khi nào thì hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b (a’ ≠ 0) song song với nhau, trùng nhau, cắt nhau?

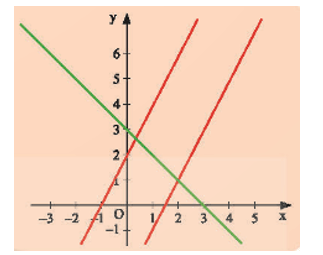
Hướng dẫn giải:

+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0 ) song song với nhau khi a = a’ và b ≠ b’.

+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0) cắt nhau khi a ≠ a’

+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’(a’ ≠ 0) trùng nhau khi a = a’ và b = b’.

1. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Khám phá 1 trang 23 Toán 8 Tập 2:

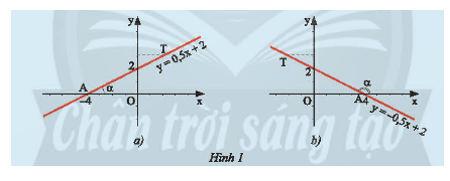
a) Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0) cắt Ox tại điểm A và T là một điểm trên đường thẳng y = ax + b (a ≠ 0) có tung độ dương (Hình 1).

Ta gọi α=$\widehat{xAT}$ là góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox. Nêu nhận xét của em về số đo của góc α và hệ số a trong hai trường hợp dưới đây.

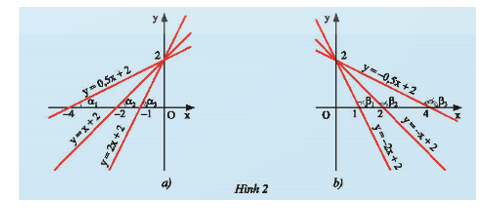
b) Hãy so sánh các hệ số a của các đường thẳng y = ax + b trong mỗi hình ở Hình 2 và so sánh các góc α hoặc các góc β tạo bởi các đường thẳng đó với trục Ox.

Hướng dẫn giải:

a) Khi a > 0 thì góc α là góc nhọn.

Khi a < 0 thì góc α là góc tù.

b) Với hệ số a dương, hệ số a càng lớn thì góc α càng lớn.

Với hế số a âm, hệ số a càng lớn thì góc β càng lớn.

Vận dụng 1 trang 24 Toán 8 Tập 2:

Trong các đường thẳng sau đây, đường thẳng nào tạo với Ox một góc nhọn, đường thẳng nào tạo với Ox một góc tù?

a) y = 3x + 6;

b) y = −4x + 1;

c) y = −3x – 6.

Hướng dẫn giải:

Những đường thẳng có a < 0 sẽ tạo với Ox một góc tù nên các đường thẳng tạo với Ox một góc tù là: y = 3x + 6.

Những đường thẳng có a > 0 sẽ tạo với Ox một góc nhọn nên các đường thẳng tạo với Ox một góc nhọn là: y = −4x + 1; y = −3x – 6.

2. Hai đường thẳng song song, hai đường thẳng cắt nhau

Khám phá 2 trang 24 Toán 8 Tập 2:

Quan sát Hình 3.

a) So sánh hệ số góc của hai đường thẳng: d: y = 2x + 3 và d’: y = 2x – 2.

Nêu nhận xét về vị trí giữa hai đường thẳng này.

b) Tìm đường thẳng d’’ đi qua gốc O và song song với đường thẳng d.

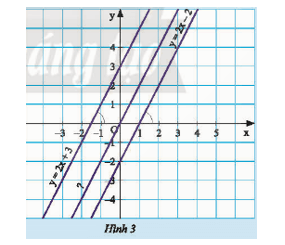
Hướng dẫn giải:

a) Hai đường thẳng: d: y = 2x + 3 và d’: y = 2x − 2 có hệ số góc bằng nhau và đều bằng 2.

Ta thấy d // d’.

b) d’’ đi qua gốc O nên d’’ có dạng y = ax mà d’’ // d suy ra a = 2.

Vậy d'': y = 2x.

Khám phá 3 trang 25 Toán 8 Tập 2:

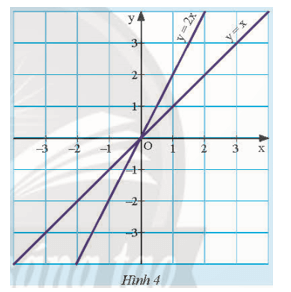
Quan sát Hình 4

a) Tìm giao điểm của hai đường thẳng d: y = 2x và d’: y = x.

b) Nêu nhận xét về hai đường thẳng có hệ số góc khác nhau.

c) Cho đường thẳng d’’: y = ax + b và cho biết d’’ cắt d. Hệ số góc a của d’’ có thể nhận các giá trị nào?

Hướng dẫn giải:

a) Ta có phương trình hoành độ giao điểm:

2x = x ⇒ x = 0 ⇒ y = 0

Vậy O(0; 0) là giao điểm của d và d’

b) Hai đường thẳng có hệ số góc khác nhau thì cắt nhau.

c) d’’ cắt d nên a ∈ ℝ\{2}.

Thực hành 2 trang 26 Toán 8 Tập 2:

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

d1: y = 3x;

d2: y = −7x + 9;

d3: y = 3x − 0,8;

d4: y = −7x – 1;

d5: y=2x+10 ;

d6: y=2x+10 .

Hướng dẫn giải:

Ba cặp đường thẳng cắt nhau: d1 và d4; d1 và d2; d1 và d5 vì hai đường thẳng trong mỗi cặp có hệ số góc khác nhau.

Các cặp đường thẳng song song: d1 và d3 (đều có a = 3); d5 và d6

(đều có a=$\sqrt{2}$); d2 và d4 (đều có a = −7).

Vận dụng 2 trang 26 Toán 8 Tập 2:

Hai ô tô khởi hành cùng lúc và cùng với tốc độ 50 km/h, một ô tô bắt đầu từ B, một ô tô bắt đầu từ C và cùng đi về phía D (Hình 5).

a) Viết công thức của hai hàm số biểu thị khoảng cách từ A đến mỗi xe sau x giờ.

b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song song.

Hướng dẫn giải:

a) Hàm số biểu thị khoảng cách từ A đến xe xuất phát từ B sau x giờ:

d1: y = f(x) = 50x + 3 (km)

Hàm số biểu thị khoảng cách từ A đến xe xuất phát từ C sau x giờ:

d2: y = g(x) = 50x + 5 (km)

b) Hai đường thẳng d1 và d2 phân biệt (cắt Oy tại hai điểm khác nhau) và có hệ số góc bằng nhau (cùng bằng 50), suy ra d1//d2.

Bài tập

Bài 1 trang 26 Toán 7 tập 2 CTST

Cho hàm số bậc nhất y = ax – 4.

a) Tìm hệ số góc a biết rằng đồ thị hàm số đi qua điểm M(1; −2).

b) Vẽ đồ thị của hàm số.

Hướng dẫn giải

a) Đồ thị hàm số đi qua điểm M(1; −2) nên ta có: −2 = a − 4 suy ra a = 2.

b) Đồ thi hàm số y = 2x − 4 đi qua hai điểm A(0; −4) và B(2; 0).

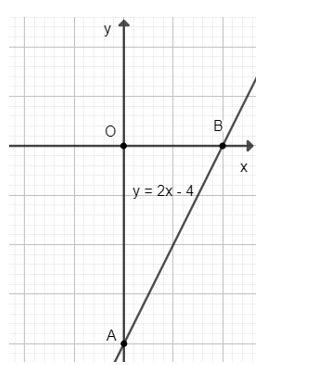
Bài 2 trang 26 Toán 7 tập 2 CTST

a) Vẽ đồ thị của hai hàm số y = x và y = x + 2 trên cùng một mặt phẳng tọa độ.

b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng y = x và y = x + 2 với trục Ox.

Hướng dẫn giải

a) Đồ thị hàm số y = x đi qua hai điểm O(0; 0) và (1; 1).

Đồ thị hàm sô y = x + 2 đi qua hai điểm có tọa độ (−2; 0) và (0; 2).

Gọi đồ thị hàm số y = x và y = x + 2 lần lượt là d1 và d2.

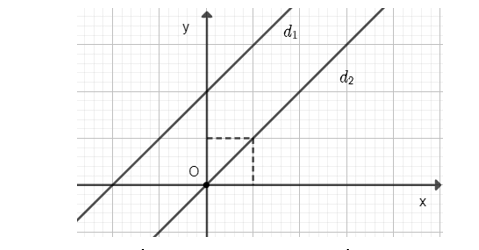
b) Góc tạo bởi d1 và Ox bằng góc tạo bởi d2 và Ox và bằng 45°.

bài 4 trang 26 Toán 7 tập 2 CTST

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

d₁: y = 0,2x; d₂: y = −2x + 4; d₃: y = 0,2x − 0,8; d₄: y = −2x − 5;.......

Hướng dẫn giải

Ba cặp đường thẳng cắt nhau: d₁ và d₂; d₂ và d₃; d₃ và d₄ (vì hai đường thẳng trong mỗi cặp có hệ số góc khác nhau).

Các cặp đường thẳng song song: d₁ và d₃ (có hế số góc đều bằng 0,2), d₂ và d₄ ( có hệ số góc đều bằng −2); d₅ và d₆ ( có hệ số góc đều bằng $-\sqrt{3}$)

Bài 4 trang 26 Toán 7 tập 2 CTST

Tìm hệ số góc a để hai đường thẳng y = ax + 2 và y = 9x – 9 song song với nhau.

Hướng dẫn giải

Hai đường thẳng y = ax + 2 và y = 9x – 9 song song với nhau nên có hệ số góc bằng nhau suy ra a = 9.

Bài 5 trang 26 Toán 7 tập 2 CTST

Cho hai hàm số bậc nhất y = 2mx – 5 và y = 2x + 1. Với giá trị nào của m thì đồ thị của hai hàm số đã cho là:

a) Hai đường thẳng song song với nhau?

b) Hai đường thẳng cắt nhau?

Hướng dẫn giải

a) Hai đường thẳng y = 2mx – 5 và y = 2x + 1 song song với nhau nên có hệ số góc bằng nhau suy ra m = 1

b) Hai đường thẳng y = 2mx – 5 và y = 2x + 1 song song với nhau nên có hệ số góc khác nhau suy ra m ≠ 1.

Bài 6 trang 26 Toán 7 tập 2 CTST

Cho đường thẳng d: y = x + 2023. Hãy viết phương trình hai đường thẳng song song với d.

Hướng dẫn giải

Đường thẳng song song với d: y = x + 2023 suy ra có hệ số góc bằng 1.

Ta có: d’: y = x – 23; d’’: y = x +1

Bài 7 trang 27 Toán 7 tập 2 CTST

Cho đường thẳng d: y = −x − 2022. Hãy viết phương trình hai đường thẳng cắt d.

Hướng dẫn giải

Đường thẳng cắt d: y = −x − 2022 suy ra có hệ số góc khác −1.

Ta có:

d’: y = x + 1; d’’: y = 2x + 2022.

Bài 8 trang 27 Toán 7 tập 2 CTST

Lan phụ giúp mẹ bán nước chanh, em nhận thấy số li nước chanh y bán được trong ngày và nhiệt độ trung bình x (°C) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng x và y trong bảng sau:

a) So sánh các giá trị x và y tương ứng trong bảng dữ liệu trên với tọa độ (x; y) của các điểm A, B, C, D, E, F trên mặt phẳng tọa độ trong Hình 6.

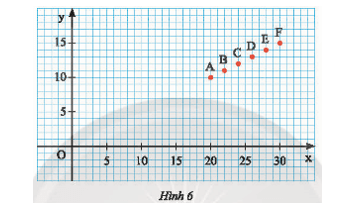
b) Cho biết đường thẳng d: y = mx đi qua các điểm A, B, C, D, E, F ở câu a. Tìm hệ số góc của d.

Hướng dẫn giải

a) Các giá trị x và y tương ứng trong bảng dữ liệu là tọa độ (x; y) của các điểm A, B, C, D, E, F trên mặt phẳng tọa độ trong Hình 6.

b) Đường thẳng d: y = mx đi qua các điểm A có tọa độ (20; 10) nên 10 = 20m suy ra m =1/2

Vậy hệ số góc của d là 1/2

Bài 9 trang 27 Toán 7 tập 2 CTST

Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Huế để đi vào thành phố Quy Nhơn với tốc độ 50 km/h.

a) Cho biết bến xe cách bưu điện thành phố Huế 4 km. Sau x giờ, xe khách cách bưu điện thành phố Huế y km. Tính y theo x.

b) Tìm hệ số góc của đường thẳng là đồ thị của hàm số y ở câu a.

Hướng dẫn giải

a) y = 50x + 4 (km)

b) Hệ số góc a = 50.

Bài 10 trang 27 Toán 7 tập 2 CTST

Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 m³ nước, mỗi giờ chảy được 1 m³.