Giải Toán 8 trang 83 tập 1 Kết nối tri thức
Giải Toán 8 trang 83 Tập 1
Giải Toán 8 trang 83 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 83.
Luyện tập trang 83 Toán 8 tập 1 Kết nối
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Hướng dẫn giải:
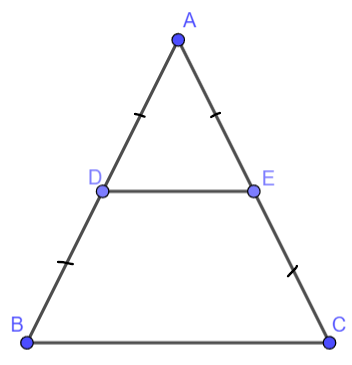
Xét Δ ABC có D, E lần lượt là trung điểm của AB và AC
Do đó DE là đường trung bình của Δ ABC
⇒ DE // BC
Xét tứ giác BDEC có: DE // BC nên BDEC là hình thang.
Mặt khác, tam giác ABC cân tại A nên 
\(\widehat{B}=\widehat{C}\)
⇒ Tứ giác BDEC là hình thang cân.
Vận dụng trang 83 Toán 8 tập 1 Kết nối
Em hãy trả lời câu hỏi trong tình huống mở đầu.
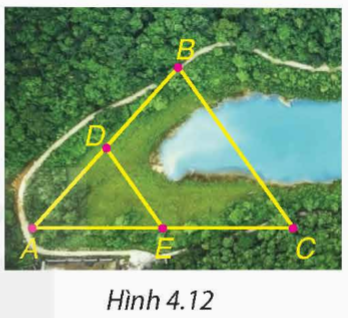
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Hướng dẫn giải:
Xét tam giác ABC có D là trung điểm của AB, E là trung điểm của AC
Do đó DE là đường trung bình của tam giác ABC.
Suy ra \(DE=\frac{1}{2}BC\)
Vậy BC = 2DE = 2 . 500 = 1 000 (m)
Bài 4.6 trang 83 Toán 8 tập 1 Kết nối
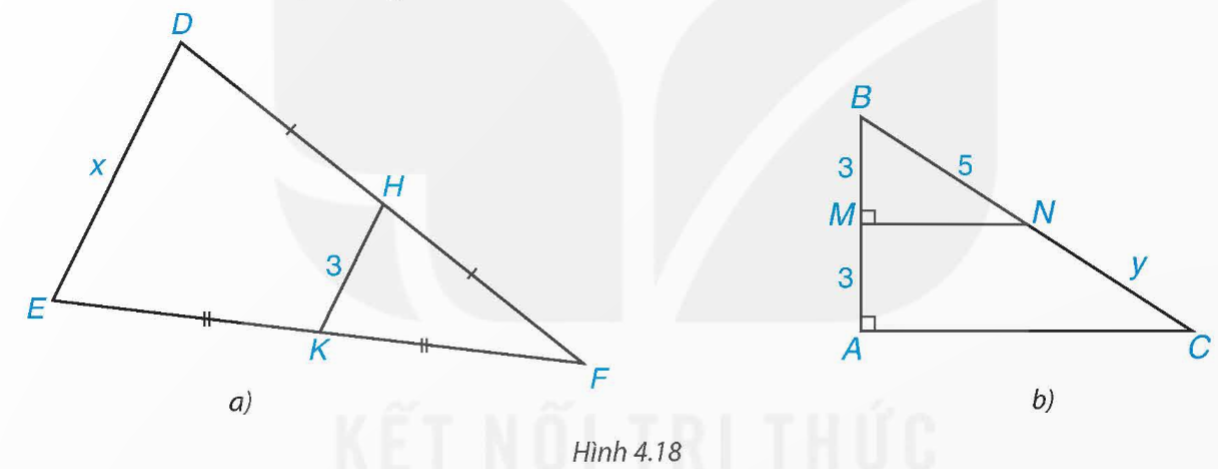
Tính các độ dài x, y trong Hình 4.18.
Hướng dẫn giải:
a) Xét tam giác DEF có H, K lần lượt là trung điểm của FD và FE
Do đó HK là đường trung bình của tam giác DEF
Suy ra \(HK=\frac{1}{2}DE=\frac{1}{2}x =3\)
Vậy x = 6.
b) Ta có: NM ⊥ AB, AC ⊥ AB nên MN // AC
Mặt khác MN đi qua trung điểm M của AB
Suy ra MN cũng đi qua trung điểm N của BC
Vậy y = BN = 5
Bài 4.7 trang 83 Toán 8 tập 1 Kết nối
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang
b) Tứ giác MNPB là hình gì? Tại sao?
Hướng dẫn giải:
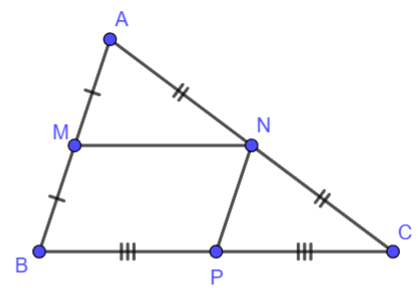
a) Xét tam giác ABC có M, N lần lượt là trung điểm của AB và AC
Do đó MN là đường trung bình của Δ ABC
⇒ MN // BC
Xét tứ giác BMNC có MN // BC nên BMNC là hình thang.
b) Chứng minh tương tự, ta có NP là đường trung bình của tam giác ABC
⇒ NP // AB
Xét tứ giác BMNP có MN // BP và NP // MB
Suy ra BMNP là hình bình hành.
Bài 4.8 trang 83 Toán 8 tập 1 Kết nối
Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E
a) Chứng minh DC // EM
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Hướng dẫn giải:
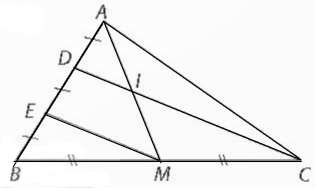
a) Xét tam giác BDC có M, E lần lượt là trung điểm của BC và BD
Do đó EM là đường trung bình của Δ BDC
⇒ ME // CD
b) Xét tam giác AEM có D là trung điểm của AE và DI // EM (CD // EM)
Suy ra I là trung điểm của AM (đpcm).
Bài 4.9 trang 83 Toán 8 tập 1 Kết nối
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật.
Hướng dẫn giải:
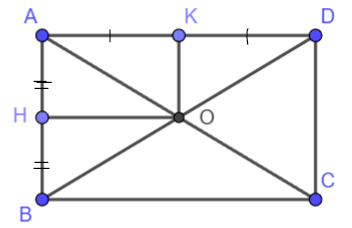
Ta có ABCD là hình chữ nhật nên OA = OB = OC = OD
Xét tam giác ABD có H, O lần lượt là trung điểm của AB và BD
Do đó OH là đường trung bình của tam giác ABD
⇒ OH // AK và OH = AK \(=\frac{1}{2}AD\)
Xét tứ giác AHOK có OH // AK và OH = AK nên AHOK là hình bình hành (dhnb)
Mặt khác \(\widehat{HAK}=90^{\circ}\)
⇒ AHOK là hình chữ nhật (dhnb).
-----------------------------------------------
Lời giải Toán 8 trang 83 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức bài 16: Đường trung bình của tam giác, được VnDoc biên soạn và đăng tải!
