Toán 8 Kết nối tri thức bài 14
Giải Toán 8 Kết nối tri thức bài 14: Hình thoi và hình vuông hướng dẫn giải các bài tập trong sgk Toán 8 Kết nối tri thức tập 1 trang 67, 68, 69, 70, 71, 72, giúp các em nắm vững kiến thức được học và luyện giải Toán 8 hiệu quả. Mời các em cùng tham khảo để nắm được nội dung bài học.
Bài 14: Hình thoi và hình vuông
Mở đầu trang 67 Toán 8 Tập 1:
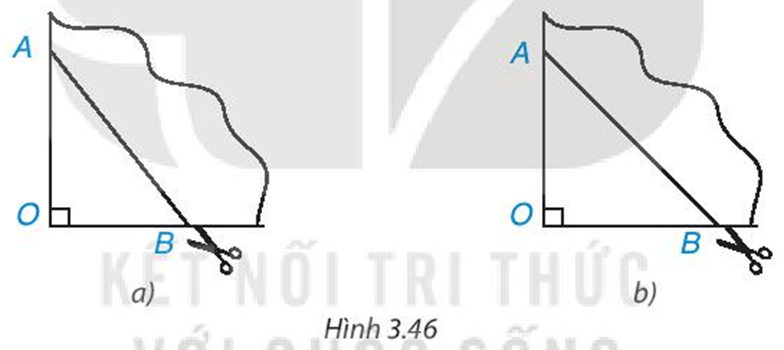
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt chéotheo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
Hướng dẫn giải:
Sau bài học này ta giải quyết được bài toán như sau:
• Hình 3.46a)
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
• Hình 3.46b)
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
1. Hình thoi
Câu hỏi trang 67 sgk Toán 8 tập 1 KNTT:
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Hướng dẫn giải:
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau.
Do đó hình thoi cũng là hình bình hành.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
- Hình thoi có hai góc đối bằng nhau.
- Hình thoi có các cặp cạnh đối song song.
- Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hoạt động 1 trang 68 sgk Toán 8 tập 1 KNTT:
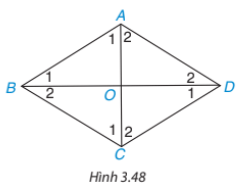
Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48)
a) 
\(\Delta ABD\) có cân tại A không?
b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?
Hướng dẫn giải:
a) Ta có AB = AD nên ABD là tam giác cân tại A
b) Ta có O là trung điểm của BD (do ABCD là hình thoi nên cũng là hình bình hành) \(\Rightarrow OB = OD\)
Xet tam giác AOB và AOD ta có:
AO chung
OB = OD
AB = AD
\(\Rightarrow \Delta AOB=\Delta AOD (c.c.c) \Rightarrow \widehat{A1}=\widehat{A2}\)
Suy ra AC là phân giác \(\widehat{A}\)
Mà tam giác ABD cân suy ra AC vuông góc với BD
Câu hỏi trang 68 Toán 8 Tập 1:
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
Hướng dẫn giải:
Giả thiết, kết luận của câu c trong Định lí 2.
Luyện tập 1 trang 69 sgk Toán 8 tập 1 KNTT:
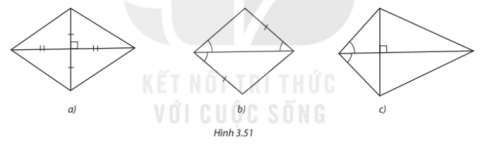
Trong Hình 3.51, hình nào là hình thoi? Vì sao?
Hướng dẫn giải:
Hình a) Vì là hình bình hành (có hai đường chéo cắt nhau ở trung điểm của mỗi đường) có hai đường chéo vuông góc với nhau
2. Hình vuông
Hoạt động 2 trang 70 sgk Toán 8 tập 1 KNTT:
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau
Hướng dẫn giải:
Vì hình vuông có bốn góc vuông nên hình vuông cũng là hình chữ nhật nên có hai đường chéo bằng nhau.
Vì hình vuông có bốn cạnh bằng nhau nên hình vuông cũng là hình thoi nên có hai đường chéo vuông góc với nhau.
Câu hỏi trang 70 Toán 8 Tập 1:
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
Hướng dẫn giải:
GT | Hình chữ nhật ABCD có AB = AD. |
KL | ABCD là hình vuông. |
Ta có thể viết giả thiết đối với cặp cạnh kề khác như: AB = BC; BC = CD; CD = AD.
Luyện tập 2 trang 71 sgk Toán 8 tập 1 KNTT:
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
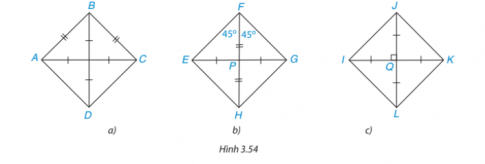
Hướng dẫn giải:
a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
b) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
c) Hình chữ nhật có hai đường chéo vuông góc
Vận dụng trang 71 Toán 8 Tập 1:
Trở lại tình huống mở đầu .
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
Hãy giải thích tại sao.
- Trong trường hợp a, ta được hình thoi.
- Trong trường hợp b, ta được hình vuông
Hướng dẫn giải:
- Trong trường hợp a:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
3. Giải bài tập trang 71 sgk Toán 8 tập 1 KNTT:
Bài tập 3.29 trang 71 sgk Toán 8 tập 1 KNTT:
Tìm các hình thoi và hình vuông trong Hình 3.55
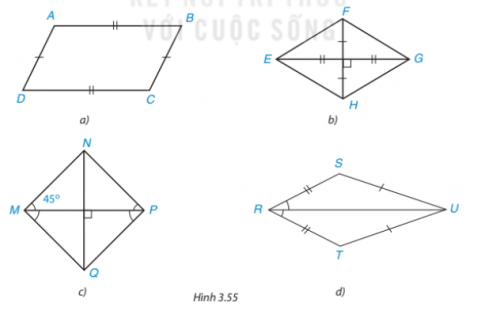
Hướng dẫn giải:
Xét tứ giác EFGH ta có: hai đường chéo cắt nhau ở trung điểm của mỗi đường \(\Rightarrow EFGH\) là hình bình hành
Lại có \(EG\perp FH\Rightarrow EFG\) là hình thoi
Xét tứ giác MNPQ ta có: các góc đều bằng \(90^{\circ}\Rightarrow MNP\) là hình chữ nhật
Lại có \(MP\perp NQ\Rightarrow MNP\) là hình vuông
Bài tập 3.30 trang 72 sgk Toán 8 tập 1 KNTT:
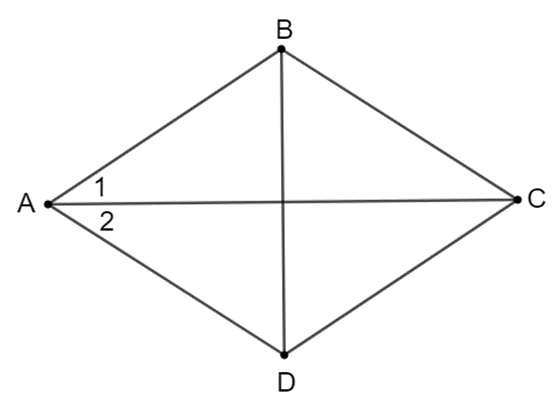
Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F
a) Tứ giác AEDF là hình gì? Vì sao?
b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?
d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị tri nào trên cạnh BC để AEDF là hình vuông?
Hướng dẫn giải:
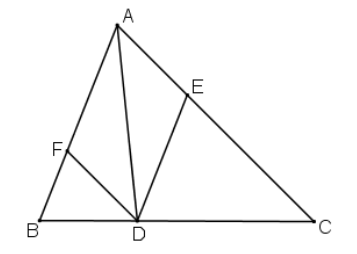
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
Mà ABC là tam giác cân tại A nên D là trung điểm của BC.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là trung điểm cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
Bài tập 3.31 trang 72 sgk Toán 8 tập 1 KNTT:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi
Hướng dẫn giải:
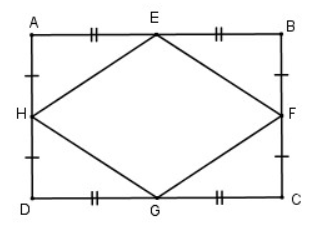
* Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
\(\Rightarrow\) EH=\(\frac{BD}{2}\) (1)
* Chứng minh tương tự, ta có:
\(FG=\frac{BD}{2};EF=\frac{AC}{2};HG=\frac{AC}{2}\) (2)
* Lại có, ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2), (3) suy ra: EF = FG = GH= HE
=> tứ giác EFGH là hình thoi.
Bài tập 3.32 trang 72 sgk Toán 8 tập 1 KNTT:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thôi là các đỉnh của một hình chữ nhật
Hướng dẫn giải:
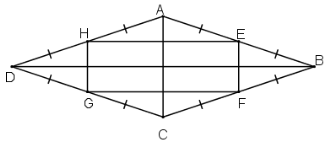
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
\(\Rightarrow EF//AC; EF=\frac{AC}{2}\) (1)
* Tương tự tam giác ADC có HG là đường trung bình nên:
HG // AC và \(HG=\frac{AC}{2}\) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
=> tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên \(\widehat{FEH}=90^{\circ}\)
Hình bình hành EFGH có \(\widehat{E}=90^{\circ}\) nên là hình chữ nhật
Bài tập 3.33 trang 72 sgk Toán 8 tập 1 KNTT:
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng \(MA\perp MD\). Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56)
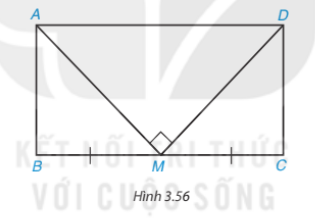
Hướng dẫn giải:
Gọi I là trung điểm AD
\(\Rightarrow MI=\frac{AD}{2}\) (do \(\Delta AMD\) vuông tại M)
Mà M là trung điểm BC nên:
MI = AB
\(\Rightarrow AB=\frac{AD}{2}\)
Mà AB + AD = \(\frac{36}{2}\)= 18 (cm)
Suy ra: \(AB=\frac{8}{1+2}=6\) (cm)
\(AD=\frac{18}{1+2}\times 2=12\)(cm)
