Toán 8 Cánh diều bài 4 trang 71, 72, 73, 74, 75, 76, 77
Giải Toán 8 Cánh diều bài 4: Đồ thị của hàm số bậc nhất y = ax + b (a khác 0) hướng dẫn trả lời câu hỏi trong SGK Toán 8 Cánh diều tập 1, giúp các em nắm vững kiến thức được học và luyện giải bài tập môn Toán lớp 8. Mời các em cùng tham khảo để nắm được nội dung bài học.
Bài 4: Đồ thị của hàm số bậc nhất y = ax + b (a khác 0)
I. Đồ thị của hàm số bậc nhất
Hoạt động 1 trang 71 sgk Toán 8 tập 1 CD: Xét hàm số y = x - 2.
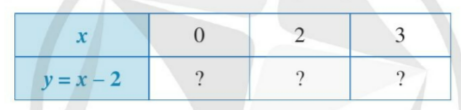
a. Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
b. Vẽ các điểm A(0; - 2), B(2; 0), C(3; 1) của thị hàm số y = x - 2 trong mặt phẳng toạ độ Oxy. Dùng thước thắng để kiểm tra ba điểm A, B, C có thẳng hàng hay không.
Bài giải
a. Tìm giá trị tương ứng của y:
| x | 0 | 2 | 3 |
| y = x - 2 | -2 | 0 | 1 |
b.
Xác định các điểm:
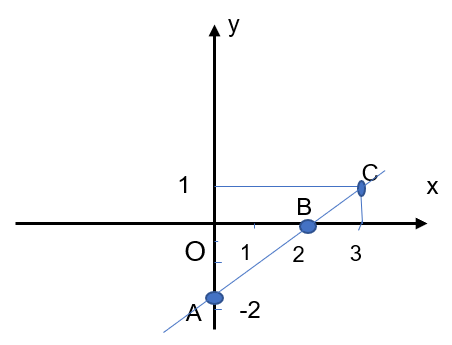
3 điểm A, B, C thẳng hàng.
Luyện tập 1 trang 72 sgk Toán 8 tập 1 CD: Cho hàm số y = 4x + 3. Tìm điểm thuộc đồ thị của hàm số có hoành độ bằng 0.
Bài giải
Điểm thuộc đồ thị của hàm số có hoành độ bằng 0 thì sẽ có tung độ là y = 4.0 + 3 = 3. Vậy điểm đó có tọa độ là (0,3)
II. Vẽ đồ thị của hàm số bậc nhất
Luyện tập 2 trang 73 sgk Toán 8 tập 1 CD: Vẽ đồ thị của mỗi hàm số sau:
a. y = 3x
b. y = 2x + 2
Bài giải
a. Với đồ thì y = 3x, ta xác định điểm A(1,3) rồi vẽ đường thẳng đi qua 2 điểm O và A
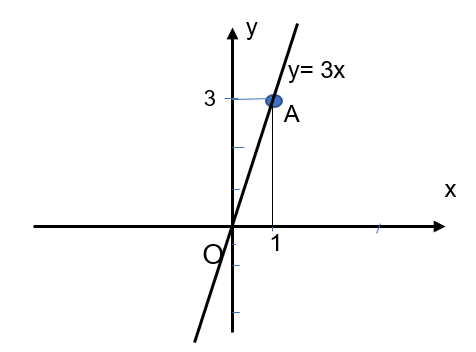
b. Với đồ thị y = 2x + 2 ta làm như sau:
+, Khi x=0 => y = 2.0+2 =2 => B(0,2)
+, Khi y=0 => x= (0-2):2 = -1 => C(-1,0)
Sau đó vẽ đường thẳng đi qua 2 điểm B và C.
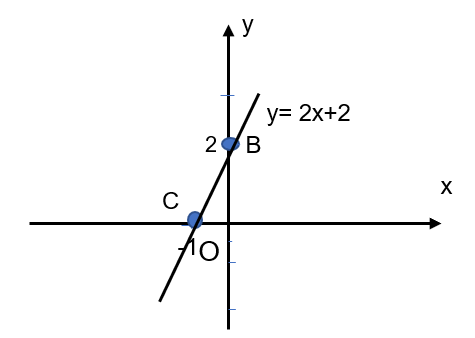
III. Hệ số góc của đường thẳng y = ax + b (a ≠0)
1. Góc tạo bởi đường thẳng y = ax + b (a≠0) với trục Ox.
Hoạt động 2 trang 73 sgk Toán 8 tập 1 CD: Quan sát các đường thẳng y = x + 1 và y = - x - 1 (hình 20)
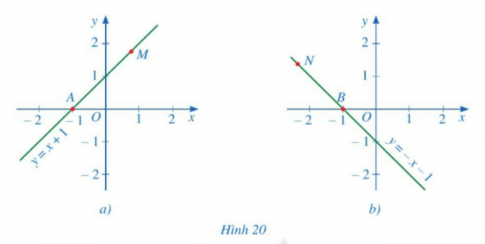
a. Tung độ các điểm M, N là số dương hay âm ?
b. Tìm góc tạo bởi 2 tia Ax và AM ở hình 20a.
c. Tìm góc tạo bởi 2 tia Bx và BN ở hình 20b.
Bài giải
a. Tung độ các điểm M, N là số dương.
b. Tìm góc tạo bởi 2 tia Ax và AM ở hình 20a: 
\(\widehat{OAM}\)
c. Tìm góc tạo bởi 2 tia Bx và BN ở hình 20b: \(\widehat{OBN}\)
2. Hệ số góc
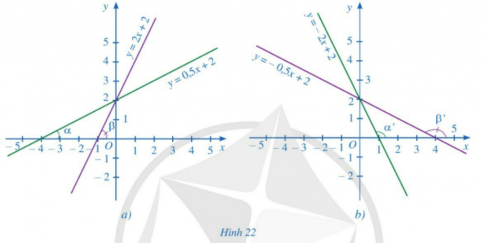
Hoạt động 3 trang 74 sgk Toán 8 tập 1 CD: Hình 22 a biểu diễn đồ thị của hàm số bậc nhất y = 0,5x + 2; y = 2x + 2. Hình 22b biểu diễn đồ thị của hàm số bậc nhất y = 2x + 2; y = -0,5x + 2.
a) Quan sát Hình 22a, so sánh các góc \(\alpha , \beta\) và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
b) Quan sát Hình 22b, so sánh các góc \(\alpha' , \beta'\) và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
Bài giải
a) Quan sát Hình 22a, các góc \(\alpha , \beta\) đều là góc nhọn và \(\alpha < \beta\)
Nhận xét: Khi hệ số a > 0 thì góc tạo bởi đường thẳng y=ax+b (a ≠0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.
b) Quan sát Hình 22b, các góc \(\alpha' , \beta'\) đều là góc tù và \(\alpha' < \beta'\)
Nhận xét: Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.
Luyện tập 3 trang 75 sgk Toán 8 tập 1 CD: Tìm hệ số góc của đường thẳng y = - 5x + 11
Bài giải
Hệ số góc của đường thẳng y = - 5x + 11 là a = - 5
3. Ứng dụng của hệ số góc
Hoạt động 4 trang 76 sgk Toán 8 tập 1 CD:
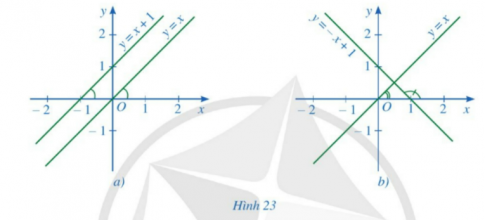
a) Quan sát Hình 23a, tìm hệ số góc của hai đường thẳng y = x và y = x + l và nêu vị trí tương đối của hai đường thẳng đó.
b) Quan sát Hình 23b, tìm hệ số góc của hai đường thẳng y = x và y = - x + 1 và nêu vị trí tương đối của hai đường thẳng đó.
Bài giải
a) Quan sát Hình 23a, Hệ số góc của hai đường thẳng:
+ y = x là a = 1
+ y = x + l là a = 1
2 đường thẳng song song với nhau
b) Quan sát Hình 23b, hệ số góc của hai đường thẳng:
+ y = x là a= 1
+ y = - x + 1 là a = -1
2 đường thẳng vuông góc với nhau.
Luyện tập 4 trang 76 sgk Toán 8 tập 1 CD: Xét vị trí tương đối của hai đường thẳng y = -5x và y = -5x + 2.
Bài giải
Hai đường thẳng y = -5x và y = -5x + 2 song song với nhau.
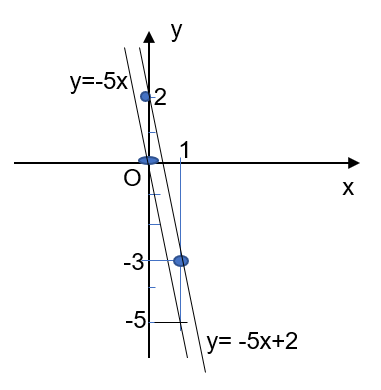
IV. Bài tập
Bài tập 1 trang 77 sgk Toán 8 tập 1 CD: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về đường thẳng d là đồ thị của hàm số y = ax + b (a ≠0)?
a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng \(-\frac{b}{a}\)
b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b
c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \(-\frac{b}{a}\)
Bài giải
Phát biểu đúng là: c, d.
Phát biểu sai là: a, b.
Bài tập 2 trang 77 sgk Toán 8 tập 1 CD: Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau: y = -2x + 5; y = -2x; y = 4x - 1
Bài giải
- Các cặp đường thẳng cắt nhau: đường thẳng y = 4x - 1 cắt 2 đường thẳng y = -2x + 5; y = -2x
- Các cặp đường thẳng song song: y = -2x + 5; y = -2x
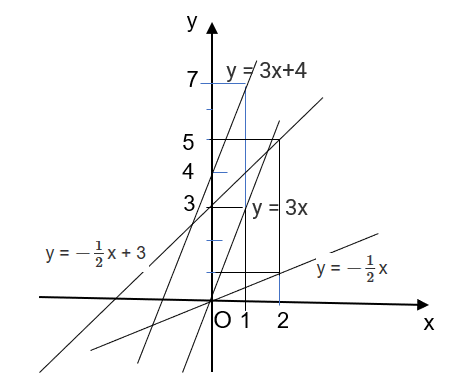
Bài tập 3 trang 77 sgk Toán 8 tập 1 CD: Vẽ đồ thị các hàm số: \(y = 3x; y = 3x + 4; y = -\frac{1}{2}x; y = -\frac{1}{2}x + 3\)
Bài giải
Cách vẽ các đường thẳng:
y = 3x đi qua 2 điểm (0,0) và (1,3)
y = 3x + 4 đi qua 2 điểm (0,4) và (1,7)
\(y = -\frac{1}{2}x\)đi qua 2 điểm (0,0) và (2,1)
\(y = -\frac{1}{2}x + 3\) đi qua 2 điểm (0,3) và (2,5)
Bài tập 4 trang 77 sgk Toán 8 tập 1 CD: Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng - 1 và đi qua điểm M(1 ; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng toạ độ.
Bài giải
Vì đường thẳng đi qua điểm M(1 ; 2) và có hệ số góc = -1 nên ta có: 2 = (-1).1+b => b = 3
Vậy đường thẳng có dạng là y = -x + 3, sẽ đi qua 1 điểm khác có tọa độ là x = 0, y=3
Bài tập 5 trang 77 sgk Toán 8 tập 1 CD:
a) Vẽ đường thẳng y = 2x - 1 trong mặt phẳng toạ độ.
b) Xác định đường thẳng y = ax + b (a ≠0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x - 1. Sau đó vẽ đường thắng tìm được trên mặt phẳng toạ độ.
Bài giải
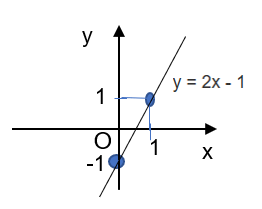
a) Vẽ đường thẳng y = 2x - 1 trong mặt phẳng toạ độ.
Đường thẳng y = 2x - 1 sẽ đi qua 2 điểm (0,-1) và (1,1)
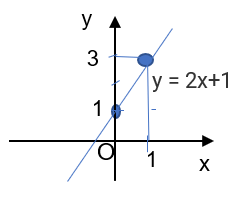
b. Đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x - 1 nên sẽ có hệ số góc a = 2, mặt khác lại đi qua điểm M(1; 3) nên ta có 3 = 2.1+b => b=1 => y = 2x + 1.
Đường thẳng này sẽ đi qua 1 điểm khác có tọa độ x = 0 và y = 1
Bài tập 6 trang 77 sgk Toán 8 tập 1 CD: Một phân đường thẳng \(d_{1}; d_{2}\) ở Hình 24 lần lượt biểu thị tốc độ (đơn vị: m/s) của vật thứ nhất, vật thứ hai theo thời gian t(s).
a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng \(d_{1}; d_{2}\). Từ đó, nêu nhận xét về tốc độ ban đầu của hai chuyển động.
b) Trong hai đường thẳng \(d_{1}; d_{2}\) đường thẳng nào có hệ số góc lớn hơn?
c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?
Bài giải
a) Hai đường thẳng \(d_{1}; d_{2}\) giao nhau tại điểm có tung độ là 2. Như vậy tốc độ ban đầu của hai chuyển động là nhu nhau và đều bằng 2 m/s.
b) Trong hai đường thẳng d1; d2 đường thẳng d2 có độ dốc lớn hơn nên có hệ số góc lớn hơn.
c) Từ giây thứ nhất trở đi, vật thứ 2 có tốc độ lớn hơn.
