Toán 8 Bài 3: Đường trung bình của tam giác

Bài 1 trang 65 Toán 8 tập 2 Cánh diều

Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn MN // BC. Chứng minh NA = NC và MN = BC.

Hướng dẫn giải

- Vì MN // BC nên theo định lí Thalès ta có:

Mà AM = MB (M là trung điểm của AB)

Suy ra: AN = NC.

- Vì MN // BC nên ta có:

Mà AM = AB (M là trung điểm của AB)

Do đó: MN = BC.

Bài 2 trang 65 Toán 8 tập 2 Cánh diều

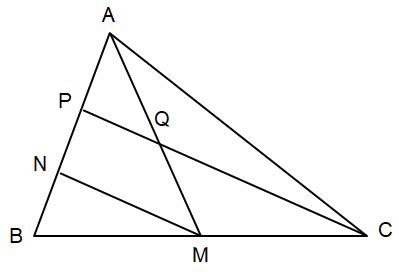
Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:

a) MN // CP;

b) AQ = QM;

c) CP = 4PQ.

Hướng dẫn giải

a) Tam giác BCP có: PN = NB; BM = MC (M là trung điểm của BC)

Suy ra:

Do đó: MN // CP (Định lí Thalès).

b) Tam giác AMN có: MN // PQ (MN // CP, Q CP)

Suy ra:

Mà AP = PN

Do đó: AQ = QM.

c) Do MN // PQ nên

Mà AP = AN

Suy ra: PQ = NM. (1)

Do MN // CP nên

Mà BN = BP

Suy ra: NM = CP. (2)

Từ (1)(2) suy ra: PQ = .CP = CP hay CP = 4PQ.

Bài 3 trang 65 Toán 8 tập 2 Cánh diều

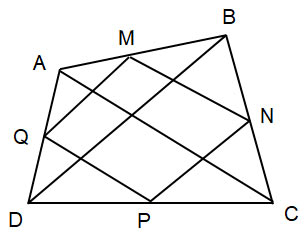
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

c) Cho AC BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

Hướng dẫn giải

a) Tam giác ABD có: M, Q lần lượt là trung điểm của AB, DA.

Suy ra: MQ là đường trung bình nên MQ // BD (1)

Tam giác BDC có: N, P lần lượt là trung điểm của BC, CD.

Suy ra: NP là đường trung bình nên NP // BD (2)

Từ (1)(2) suy ra: MQ // NP (3)

Tam giác ABC có: M, N lần lượt là trung điểm của AB, BC.

Suy ra: MN là đường trung bình nên MN // AC (4)

Tam giác ADC có: P, Q lần lượt là trung điểm của CD, DA.

Suy ra: PQ là đường trung bình nên PQ // AC (5)

Từ (4)(5) suy ra: MN // PQ (6)

Từ (3)(6) suy ra: MNPQ là hình bình hành.

b) MQ là đường trung bình của tam giác ABD, suy ra MQ = BD

NP là đường trung bình của tam giác BDC, suy ra NP = BD

MN là đường trung bình của tam giác ABC, suy ra MN = AC

PQ là đường trung bình của tam giác ADC, suy ra PQ = AC

Mà AC = BD

Do đó: MQ = NP = MN = PQ

Mà MNPQ là hình bình hành (cmt)

Suy ra: MNPQ là hình thoi.

c) Ta có: MQ // BD; MN // AC

Mà AC BD

Suy ra: MQ MN

Mà MNPQ là hình bình hành (chứng minh câu a)

Do đó: MNPQ là hình chữ nhật.

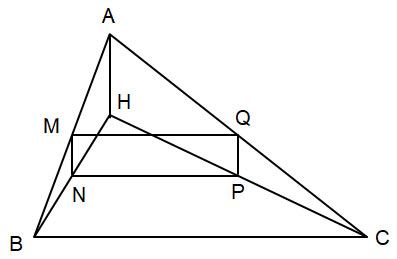
Bài 4 trang 65 Toán 8 tập 2 Cánh diều

Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Hướng dẫn giải

Tam giác ABH có: M, N lần lượt là trung điểm của AB, BH.

Suy ra: MN là đường trung bình nên MN // AH và MN = AH (1)

Tam giác ACH có: P, Q lần lượt là trung điểm của CH, AC.

Suy ra: PQ là đường trung bình nên PQ // AH và PQ = AH (2)

Từ (1)(2) suy ra: MN // PQ và MN = PQ.

Do đó: MNPQ là hình bình hành (3)

Ta có: MN // AH

Mà AH BC (H là trực tâm tam giác ABC)

Suy ra: MN BC

Mà MQ // BC (MQ là đường trung bình của tam giác ABC)

Do đó: MN MQ (4)

Từ (3)(4) suy ra: MNPQ là hình chữ nhật.

Bài 5 trang 65 Toán 8 tập 2 Cánh diều

Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số 1 và số 2, từ đó ước lượng được độ dài đoạn thẳng MN khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC. Hỏi khoảng cách đó khoảng bao nhiêu mét?

Hướng dẫn giải

Ta có: MN là đường trung bình của tam giác ABC nên MN = BC hay BC = 2MN

Mà khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC

Suy ra: Khoảng cách đó bằng 2MN hay bằng 2.4,5 = 9 m.