Toán 8 Kết nối tri thức bài 16: Đường trung bình của tam giác
Giải Toán 8 Kết nối tri thức Bài 16: Đường trung bình của tam giác cung cấp hướng dẫn giải chi tiết và đáp án cụ thể cho toàn bộ các bài tập nằm trong Sách giáo khoa Toán 8, tập 1 (từ trang 81, 82 đến 83) thuộc bộ sách Kết nối tri thức với cuộc sống.
Nội dung giải không chỉ đưa ra kết quả cuối cùng mà còn trình bày từng bước giải quyết vấn đề một cách logic và khoa học, giúp các em hiểu rõ cách áp dụng định lý về đường trung bình của tam giác và hình thang. Việc tham khảo tài liệu này sẽ giúp học sinh nắm vững kiến thức trọng tâm, luyện tập kỹ năng giải Toán hình học một cách hiệu quả, và tự tin hơn khi đối diện với các dạng bài tập liên quan. Mời các em tham khảo để củng cố nền tảng Toán học của mình.
Giải Toán 8 KNTT bài 16: Đường trung bình của tam giác
1. Định nghĩa đường trung bình của tam giác
Câu hỏi trang 81 sgk Toán 8 tập 1 KNTT:
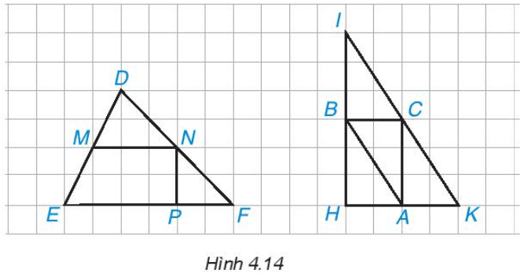
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Lời giải:
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆IHK.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆IHK.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆IHK.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
2. Tính chất đường trung bình của tam giác
Hoạt động 1 trang 82 sgk Toán 8 tập 1 KNTT:
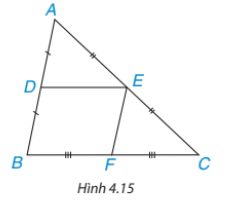
Cho DE là đường trung bình của tam giác ABC (H.4.15).Sử dụng định lí Thales đảo, chứng minh rằng DE // BC
Hướng dẫn giải:
Ta có: D là trung điểm của AB nên 
\(\frac{AD}{AB}=\frac{1}{2}\)
E là trung điểm của AC nên \(\frac{AE}{AC}=\frac{1}{2}\)
Suy ra \(\frac{AD}{AB}=\frac{AE}{AC}\) do đó DE // BC
Hoạt động 2 trang 82 sgk Toán 8 tập 1 KNTT:
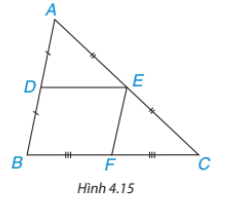
Cho DE là đường trung bình của tam giác ABC (H.4.15). Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra \(DE=\frac{1}{2}BC\)
Hướng dẫn giải:
Ta có: F là trung điểm của BC nên \(\frac{BF}{BC}=\frac{1}{2}\)
E là trung điểm của AC nên \(\frac{AE}{AC}=\frac{1}{2}\)
Suy ra \(\frac{BF}{BC}=\frac{AE}{AC}\) do đó EF // AB
Xét tứ giác DEFB ta có: DE // BF, EF // DB suy ra DEFB là hình bình hành \(\Rightarrow DE=BF\)
Mà \(BF=\frac{1}{2}BC\) suy ra \(DE=\frac{1}{2}BC\)
Luyện tập trang 83 sgk Toán 8 tập 1 KNTT:
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Hướng dẫn giải:
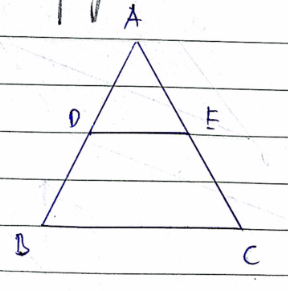
ΔABC có: DA=DB(gt)
EA=EC(gt)
=> DE là đường trung bình của ΔABC
=> DE//BC
Xét tứ giác BDEC có: DE//BC
=> Tứ giác BDEC là hình thang
Mà: \(\widehat{B}=\widehat{C}\) (gt)
=> Tứ giác BDEC là hình thang cân
Vận dụng trang 83 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu.
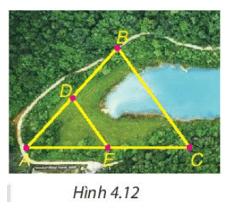
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Hướng dẫn giải:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.Suy ra DE là đường trung bình của tam giác ABC.
Do đó DE = \(\frac{1}{2}\)BC suy ra BC = 2DE = 2 . 500 = 1 000 (m)
3. Bài tập trang 83 sgk Toán 8 tập 1 KNTT:
Bài tập 4.6 trang 83 sgk Toán 8 tập 1 KNTT:
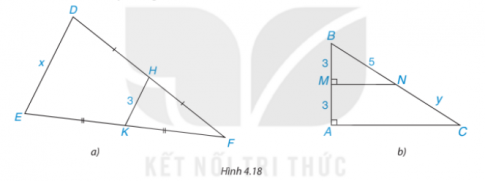
Tính các độ dài x, y trong Hình 4.18.
Hướng dẫn giải:
a) HK là đường trung bình suy ra \(HK=\frac{1}{2}DE=\frac{1}{2}x\Rightarrow x=6\)
b) Ta có: \(NM\perp AB,AC\perp AB\Rightarrow MN//A\)
Mặt khác M là trung điểm AB nên MN là đường trung bình của tam giác ABC
Suy ra N là trung điểm BC ⇒ y = BN = 5
Bài tập 4.7 trang 83 sgk Toán 8 tập 1 KNTT:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang
b) Tứ giác MNPB là hình gì? Tại sao?
Hướng dẫn giải:
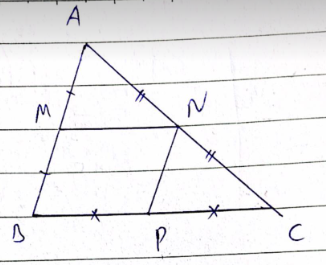
a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
suy ra MN // BC
Do đó tứ giác BMNC là hình thang
b) Ta có: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\frac{BC}{2}\)
mà \(BP=\frac{BC}{2}\)
nên MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
Bài tập 4.8 trang 83 sgk Toán 8 tập 1 KNTT:
Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E
a) Chứng minh DC // EM
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM
Hướng dẫn giải:
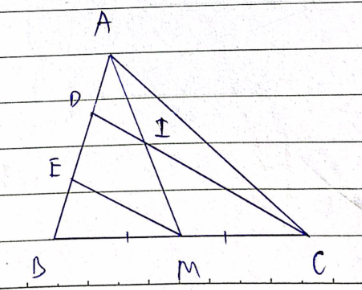
a) Xét ΔBDC có
E là trung điểm của BD(BE=ED; B,E,D thẳng hàng)
M là trung điểm của BC(gt)
Do đó: EM là đường trung bình của ΔBDC (Định nghĩa đường trung bình của tam giác)
⇒ ME//CD (Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE(AD=DE; A,D,E thẳng hàng)
DI//EM (cmt)
Do đó: I là trung điểm của AM (Định lí 1 về đường trung bình của tam giác)
nên AI=IM (đpcm)
Bài tập 4.9 trang 83 sgk Toán 8 tập 1 KNTT:
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật
Hướng dẫn giải:
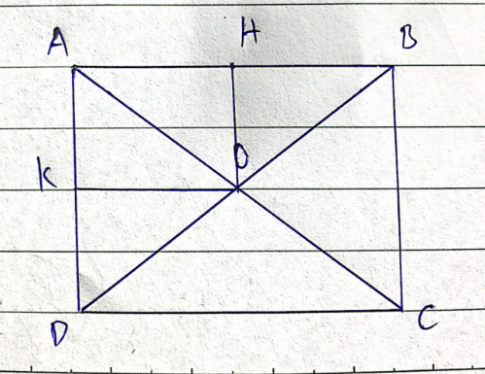
Ta có: OA = OB suy ra tam giác OAB cân tại B, OH là đường trung tuyến nên OH cũng là đường cao, do đó \(\widehat{OHA}=90^{\circ}\)
Tương tự, \(\widehat{OKA}=90^{\circ}\)
Xét tứ giác AHOK có: \(\widehat{A}=\widehat{OKA}=\widehat{OHA}=90^{\circ}\) suy ra AHOK là hình chữ nhật
